
Find the linear convolution given the following input and impulse response of a linear shift invariant system

Hence \(y\left ( n\right ) \) becomes

By Explicitly evaluating the convolution sum, evaluate the following \(y\left ( n\right ) =h\left ( n\right ) \circledast x\left ( n\right ) \)\[ h\left ( n\right ) =\left \{ \begin{array} [c]{c}\alpha ^{n}\ \ \ \ \ 0\leq n<N\\ 0\ \ \ \ \ \ \ elsewhere \end{array} \right . \] \[ x\left ( n\right ) =\left \{ \begin{array} [c]{c}\beta ^{n-n_{0}}\ \ \ \ \ n_{0}\leq n\\ 0\ \ \ \ \ \ \ n<n_{0}\end{array} \right . \] use \(N=4,n_{0}=0\)
Solution: I will evaluate \(h\left ( n\right ) \circledast x\left ( n\right ) \) by flipping \(h\left ( n\right ) \), i.e. \(h\left ( n\right ) \circledast x\left ( n\right ) ={\displaystyle \sum \limits _{k=-\infty }^{\infty }} x\left ( k\right ) h\left ( n-k\right ) \)
There are 3 regions to consider.
One when \(n<0\). In this region there are no overlapping between \(h\left ( -k\right ) \) and \(x\left ( k\right ) \), hence \(y\left ( n\right ) =0\) for \(n<0\).
The second region where there is partial overlapping, and this region extends from \(n=0\) to \(n=N-1\). Hence over this region\begin{align*} y\left ( n\right ) & ={\displaystyle \sum \limits _{k=0}^{n}} \alpha ^{-\left ( k-n\right ) }\beta ^{k}\\ & ={\displaystyle \sum \limits _{k=0}^{n}} \alpha ^{n-k}\beta ^{k}\\ & =\alpha ^{n}{\displaystyle \sum \limits _{k=0}^{n}} \alpha ^{-k}\beta ^{k}=\alpha ^{n}{\displaystyle \sum \limits _{k=0}^{n}} \left ( \frac{\beta }{\alpha }\right ) ^{k}\\ & =\alpha ^{n}\frac{1-\left ( \frac{\beta }{\alpha }\right ) ^{n+1}}{1-\frac{\beta }{\alpha }}\ \ \ \ \ \ \ \ \ \ \ \ 0\leq n\leq N-1 \end{align*}
If \(\left \vert \frac{\beta }{\alpha }\right \vert <1\) and \(N\) very large, the above simplifies to \(\frac{\alpha ^{n}}{1-\frac{\beta }{\alpha }}\).
The third region is when \(h\left ( -k\right ) \) is completely inside \(x\left ( k\right ) \) and this occurs when \(n\geq N-1\) and over this region we have \begin{align} y\left ( n\right ) & ={\displaystyle \sum \limits _{k=n-\left ( N-1\right ) }^{n}} \alpha ^{-\left ( k-n\right ) }\beta ^{k}\nonumber \\ & =\alpha ^{n}{\displaystyle \sum \limits _{k=n-\left ( N-1\right ) }^{n}} \left ( \frac{\beta }{\alpha }\right ) ^{k} \tag{1} \end{align}
But \[{\displaystyle \sum \limits _{k=a}^{b}} r^{k}=\frac{r^{b+1}-r^{a}}{r-1}\] hence (1) becomes \begin{align*} y\left ( n\right ) & =\alpha ^{n}\frac{\left ( \frac{\beta }{\alpha }\right ) ^{n+1}-\left ( \frac{\beta }{\alpha }\right ) ^{n-\left ( N-1\right ) }}{\left ( \frac{\beta }{\alpha }\right ) -1}\\ & =\alpha ^{n}\frac{\left ( \frac{\beta }{\alpha }\right ) ^{n}\left ( \frac{\beta }{\alpha }\right ) -\left ( \frac{\beta }{\alpha }\right ) ^{n}\left ( \frac{\beta }{\alpha }\right ) ^{-N}\left ( \frac{\beta }{\alpha }\right ) }{\left ( \frac{\beta }{\alpha }\right ) -1} \end{align*}
Divide by \(\left ( \frac{\beta }{\alpha }\right ) \)\begin{align*} y\left ( n\right ) & =\alpha ^{n}\frac{\left ( \frac{\beta }{\alpha }\right ) ^{n}-\left ( \frac{\beta }{\alpha }\right ) ^{n}\left ( \frac{\beta }{\alpha }\right ) ^{-N}}{1-\frac{\alpha }{\beta }}\\ & =\alpha ^{n}\left ( \frac{\beta }{\alpha }\right ) ^{n}\frac{1-\left ( \frac{\alpha }{\beta }\right ) ^{N}}{1-\frac{\alpha }{\beta }}\\ & =\beta ^{n}\frac{1-\left ( \frac{\alpha }{\beta }\right ) ^{N}}{1-\frac{\alpha }{\beta }} \end{align*}
Now consider the term \(\frac{\alpha }{\beta }\). If \(\left \vert \frac{\alpha }{\beta }\right \vert <1\), then the above will become \(\frac{\beta ^{n}}{1-\frac{\alpha }{\beta }}.\) hence to summarize the general solution: \[ y\left ( n\right ) =\left \{ \begin{array} [c]{cc}0 & n<0\\ & \\ & \\ \alpha ^{n}\frac{1-\left ( \frac{\beta }{\alpha }\right ) ^{n+1}}{1-\frac{\beta }{\alpha }} & 0\leq n\leq N-1\\ \frac{\alpha ^{n}}{1-\frac{\beta }{\alpha }} & 0\leq n\leq N-1\text{ and }\left \vert \frac{\beta }{\alpha }\right \vert <1\text{ and }N\ \text{very large}\\ & \\ & \\ \beta ^{n}\frac{1-\left ( \frac{\alpha }{\beta }\right ) ^{N}}{1-\frac{\alpha }{\beta }} & n\geq N-1\\ \frac{\beta ^{n}}{1-\frac{\alpha }{\beta }} & n\geq N-1\text{\ \ and }\left \vert \frac{\alpha }{\beta }\right \vert <1\text{ and }N\ \text{very large}\end{array} \right . \] Since \(N=4\) in this problem, the specific solution is\[ y\left ( n\right ) =\left \{ \begin{array} [c]{cc}0 & n<0\\ \alpha ^{n}\frac{1-\left ( \frac{\beta }{\alpha }\right ) ^{n+1}}{1-\frac{\beta }{\alpha }} & 0\leq n\leq N-1\\ \beta ^{n}\frac{1-\left ( \frac{\alpha }{\beta }\right ) ^{N}}{1-\frac{\alpha }{\beta }} & n\geq N-1 \end{array} \right . \] For example, for \(N=4,\alpha =.9,\beta =.8\), the following is a plot for up to \(n=50\)
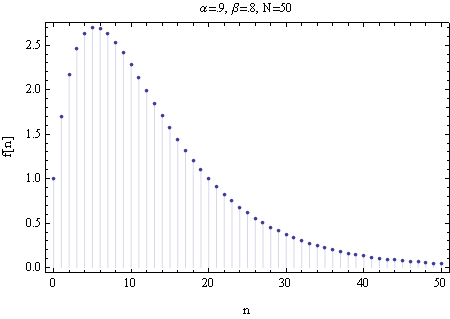
code used to generate the above plot is
Let \(e\left ( n\right ) \) be an exponential sequence \(e\left ( n\right ) =\alpha ^{n}\) for all n, and let \(x\left ( n\right ) \) and \(y\left ( n\right ) \) denote 2 arbitrary sequences. Show that \(\left [ e\left ( n\right ) x\left ( n\right ) \right ] \circledast \left [ e\left ( n\right ) y\left ( n\right ) \right ] =e\left ( n\right ) \left [ x\left ( n\right ) \circledast y\left ( n\right ) \right ] \)
Solution\begin{align*} \left [ e\left ( n\right ) x\left ( n\right ) \right ] \circledast \left [ e\left ( n\right ) y\left ( n\right ) \right ] & =\alpha ^{n}x\left ( n\right ) \circledast \alpha ^{n}y\left ( n\right ) \\ & ={\displaystyle \sum \limits _{k=-\infty }^{\infty }} \overbrace{\alpha ^{k}x\left ( k\right ) }\overbrace{\alpha ^{n-k}y\left ( n-k\right ) }\\ & ={\displaystyle \sum \limits _{k=-\infty }^{\infty }} \alpha ^{k}\alpha ^{n-k}x\left ( k\right ) y\left ( n-k\right ) \\ & ={\displaystyle \sum \limits _{k=-\infty }^{\infty }} \alpha ^{n}x\left ( k\right ) y\left ( n-k\right ) \end{align*}
Move \(\alpha ^{n}\) outside the summation since does not depend on \(k\), we obtain\[ \left [ e\left ( n\right ) x\left ( n\right ) \right ] \circledast \left [ e\left ( n\right ) y\left ( n\right ) \right ] =\alpha ^{n}{\displaystyle \sum \limits _{k=-\infty }^{\infty }} x\left ( k\right ) y\left ( n-k\right ) \] But \({\displaystyle \sum \limits _{k=-\infty }^{\infty }} x\left ( k\right ) y\left ( n-k\right ) =x\left ( n\right ) \circledast y\left ( n\right ) \), hence the above becomes\begin{align*} \left [ e\left ( n\right ) x\left ( n\right ) \right ] \circledast \left [ e\left ( n\right ) y\left ( n\right ) \right ] & =\alpha ^{n}\left [ x\left ( n\right ) \circledast y\left ( n\right ) \right ] \\ & =e\left ( n\right ) \left [ x\left ( n\right ) \circledast y\left ( n\right ) \right ] \end{align*}
Prove \(\left ( X\circledast Y\right ) \circledast W=X\circledast \left ( Y\circledast W\right ) \)
Solution \begin{align*} \left ( X\circledast Y\right ) \circledast W & ={\displaystyle \sum \limits _{k=-\infty }^{\infty }} \left ( X\circledast Y\right ) \left ( k\right ) \ W\left ( n-k\right ) \\ & ={\displaystyle \sum \limits _{k=-\infty }^{\infty }} \left ({\displaystyle \sum \limits _{l=-\infty }^{\infty }} X\left ( l\right ) Y\left ( k-l\right ) \right ) W\left ( n-k\right ) \end{align*}
Move \(W\left ( n-k\right ) \) inside the inner sum\begin{align*} \left ( X\circledast Y\right ) \circledast W & ={\displaystyle \sum \limits _{k=-\infty }^{\infty }} \left ({\displaystyle \sum \limits _{l=-\infty }^{\infty }} X\left ( l\right ) Y\left ( k-l\right ) W\left ( n-k\right ) \right ) \\ & ={\displaystyle \sum \limits _{k=-\infty }^{\infty }} \left ({\displaystyle \sum \limits _{l=-\infty }^{\infty }} X\left ( l\right ) W\left ( n-k\right ) Y\left ( k-l\right ) \right ) \end{align*}
Since summation indices are just dummy variable, we can rename them. Let \(k\) be renamed to \(l\) and let \(l\) be renamed to \(k\) (this can be done in 2 steps using a temporary variable if needed to avoid confusion). This is equivalent to interchanging the order of integrals in the continuous time domain case.
After this name switching of the dummy variables we obtain\[ \left ( X\circledast Y\right ) \circledast W={\displaystyle \sum \limits _{l=-\infty }^{\infty }} \left ({\displaystyle \sum \limits _{k=-\infty }^{\infty }} X\left ( k\right ) W\left ( n-l\right ) Y\left ( l-k\right ) \right ) \] Now \(W\left ( n-l\right ) \) inside the inner sum do not depend on the summation index \(k\), so we can take it outside the inner sum\[ \left ( X\circledast Y\right ) \circledast W={\sum \limits _{l=-\infty }^{\infty }}\left ({\overbrace{{\sum \limits _{k=-\infty }^{\infty }}X\left ( k\right ) Y\left ( l-k\right ) }}^{\left ( X\circledast Y\right ) (l)}\right ) W\left ( n-l\right ) \] But now we see that \({\displaystyle \sum \limits _{k=-\infty }^{\infty }} X\left ( k\right ) Y\left ( l-k\right ) \) is just \(\left ( X\circledast Y\right ) \left ( l\right ) \) hence the above becomes\[ \left ( X\circledast Y\right ) \circledast W={\displaystyle \sum \limits _{l=-\infty }^{\infty }} \left ( X\circledast Y\right ) \left ( l\right ) W\left ( n-l\right ) \] But the above is a convolution sum. Hence\[ \left ( X\circledast Y\right ) \circledast W=\left ( X\circledast Y\right ) \circledast W \] Which is what we are asked to show.
Find causal solution for the 2-sided difference equation \(y\left ( n\right ) -2.5y\left ( n-1\right ) +y\left ( n-2\right ) =\delta \left ( n\right ) \) for \(-\infty <n<\infty \)
Solution
Let \(Y\left ( z\right ) \) be the \(Z\) transform of \(y\left ( n\right ) \). In addition, since we are told that the system is causal, and the input occurs at \(n=0\) only (it is a delta function), then this means that \(y\left ( n\right ) =0\) for \(n<0\).
Now take the Z transform of the above difference equation we obtain\[ Y\left ( z\right ) -(2.5z^{-1}Y\left ( z\right ) +y\left ( -1\right ) )+\left ( z^{-2}Y\left ( z\right ) +z^{-1}y\left ( -1\right ) +y\left ( -2\right ) \right ) =1 \] But the system is causal, hence \(y\left ( -1\right ) =0\) and \(y\left ( -2\right ) =0\), the above becomes\begin{align*} Y\left ( z\right ) \left ( 1-2.5z^{-1}+z^{-2}\right ) & =1\\ Y\left ( z\right ) & =\frac{1}{1-2.5z^{-1}+z^{-2}} \end{align*}
Solve by partial fractions expansion. \(\left ( 1-2.5z^{-1}+z^{-2}\right ) =\left ( z^{-1}-\frac{1}{2}\right ) \left ( z^{-1}-2\right ) \), hence the above becomes\begin{align*} Y\left ( z\right ) & =\frac{1}{\left ( z^{-1}-\frac{1}{2}\right ) \left ( z^{-1}-2\right ) }\\ & =\frac{1}{\left ( \frac{1}{2}-z^{-1}\right ) \left ( 2-z^{-1}\right ) }\\ & =\frac{1}{\left ( 1-2z^{-1}\right ) \left ( 1-\frac{1}{2}z^{-1}\right ) }\\ & =\frac{A}{\left ( 1-2z^{-1}\right ) }+\frac{B}{\left ( 1-\frac{1}{2}z^{-1}\right ) } \end{align*}
Hence\[ \frac{1}{\left ( 1-2z^{-1}\right ) \left ( 1-\frac{1}{2}z^{-1}\right ) }=\frac{A}{\left ( 1-2z^{-1}\right ) }+\frac{B}{\left ( 1-\frac{1}{2}z^{-1}\right ) }\] Therefore, \[ A=\lim _{z^{-1}\rightarrow \frac{1}{2}}\frac{1}{\left ( 1-\frac{1}{2}z^{-1}\right ) }=\frac{1}{\frac{3}{4}}=\frac{4}{3}\] And\[ B=\lim _{z^{-1}\rightarrow 2}\frac{1}{\left ( 1-2z^{-1}\right ) }=-\frac{1}{3}\] Hence \[ Y\left ( z\right ) =\frac{4}{3}\frac{1}{\left ( 1-2z^{-1}\right ) }-\frac{1}{3}\frac{1}{\left ( 1-\frac{1}{2}z^{-1}\right ) }\] Hence\[ y\left ( n\right ) =\frac{4}{3}\left ( 2\right ) ^{n}u\left ( n\right ) -\frac{1}{3}\left ( \frac{1}{2}\right ) ^{n}u\left ( n\right ) \] But the above solution is not stable since the first term above \(\frac{4}{3}\left ( 2\right ) ^{n}u\left ( n\right ) \) blows up for large \(n\). I can find an anti causal solution which is stable, by making the first term \(-\frac{4}{3}\left ( 2\right ) ^{n}u\left ( -n-1\right ) \), but the problem said the system is causal. So I will stop here.
Hence the final solution is\[ y\left ( n\right ) =\frac{4}{3}\left ( 2\right ) ^{n}u\left ( n\right ) -\frac{1}{3}\left ( \frac{1}{2}\right ) ^{n}u\left ( n\right ) \] And it is an unstable system.
Solve the one sided difference equation \[ y(n) - y(n-1) + \frac{2}{9} y(n-2) = x(n) - x(n-1) \] for \(n\geq 0\) where the input is given by \(\delta \left ( n\right ) \) and the IC are given by \(y\left ( -1\right ) =1,y\left ( -2\right ) =0\)
solution
Let \(Y\left ( z\right ) \) be the \(Z\) transform of \(y\left ( n\right ) \) and \(X\left ( z\right ) \) be the \(Z\) transform of the input.
Take the \(Z\) transform of both side, we obtain\[ Y\left ( z\right ) -\left [ z^{-1}Y\left ( z\right ) +y\left ( -1\right ) \right ] +\frac{2}{9}\left [ z^{-2}Y\left ( z\right ) +z^{-1}y\left ( -1\right ) +y\left ( -2\right ) \right ] =X\left ( z\right ) -\left [ z^{-1}X\left ( z\right ) +x\left ( -1\right ) \right ] \] But the input \(x\left ( n\right ) \) is \(\delta \left ( n\right ) \), hence its \(Z\) transform is \(1\). And \(x\left ( -1\right ) =\) \(\delta \left ( -1\right ) =0\) by definition. In addition, substitute the initial conditions for \(y\left ( n\right ) \) in the above equation and it simplifies to\begin{align*} Y\left ( z\right ) -\left [ z^{-1}Y\left ( z\right ) +1\right ] +\frac{2}{9}\left [ z^{-2}Y\left ( z\right ) +z^{-1}+0\right ] & =1-\left [ z^{-1}\times 1+0\right ] \\ Y\left ( z\right ) -z^{-1}Y\left ( z\right ) -1+\frac{2}{9}z^{-2}Y\left ( z\right ) +\frac{2}{9}z^{-1} & =1-z^{-1}\\ Y\left ( z\right ) \left ( 1-z^{-1}+\frac{2}{9}z^{-2}\right ) & =1-z^{-1}+1-\frac{2}{9}z^{-1}\\ Y\left ( z\right ) & =\frac{2-\frac{11}{9}z^{-1}}{1-z^{-1}+\frac{2}{9}z^{-2}}\\ & =\frac{9-\frac{11}{2}z^{-1}}{\frac{9}{2}-\frac{9}{2}z^{-1}+z^{-2}} \end{align*}
Now, to find \(y(n)\) we need to inverse Z transform the above.\begin{align*} Y\left ( z\right ) & =\frac{9-\frac{11}{2}z^{-1}}{\left ( z^{-1}-3\right ) \left ( z^{-1}-\frac{3}{2}\right ) }\\ & =\frac{A}{\left ( z^{-1}-3\right ) }+\frac{B}{\left ( z^{-1}-\frac{3}{2}\right ) } \end{align*}
Hence\[ \frac{9-\frac{11}{2}z^{-1}}{\left ( z^{-1}-3\right ) \left ( z^{-1}-\frac{3}{2}\right ) }=\frac{A}{\left ( z^{-1}-3\right ) }+\frac{B}{\left ( z^{-1}-\frac{3}{2}\right ) }\] Therefore\[ A=\lim _{z^{-1}\rightarrow 3}\frac{9-\frac{11}{2}z^{-1}}{\left ( z^{-1}-\frac{3}{2}\right ) }=\frac{9-\frac{11}{2}3}{\left ( 3-\frac{3}{2}\right ) }=\frac{18-33}{\frac{3}{2}}=\frac{18-33}{3}=-5 \] And\[ B=\lim _{z^{-1}\rightarrow \frac{3}{2}}\frac{9-\frac{11}{2}z^{-1}}{\left ( z^{-1}-3\right ) }=\frac{9-\frac{11}{2}\times \frac{3}{2}}{\left ( \frac{3}{2}-3\right ) }=\frac{9-\frac{33}{4}}{-\frac{3}{2}}=\frac{36-33}{-6}=-\frac{1}{2}\] Hence\begin{align*} Y\left ( z\right ) & =-5\frac{1}{\left ( z^{-1}-3\right ) }-\frac{1}{2}\frac{1}{\left ( z^{-1}-\frac{3}{2}\right ) }\\ & =-5\frac{\frac{1}{3}}{\left ( \frac{1}{3}z^{-1}-1\right ) }-\frac{1}{2}\frac{\frac{2}{3}}{\left ( \frac{2}{3}z^{-1}-1\right ) }\\ & =-\frac{5}{3}\frac{1}{\left ( \frac{1}{3}z^{-1}-1\right ) }-\frac{1}{3}\frac{1}{\left ( \frac{2}{3}z^{-1}-1\right ) }\\ & =\frac{5}{3}\frac{1}{\left ( 1-\frac{1}{3}z^{-1}\right ) }+\frac{1}{3}\frac{1}{\left ( 1-\frac{2}{3}z^{-1}\right ) } \end{align*}
Therefore\[ y\left ( n\right ) =\frac{5}{3}\left ( \frac{1}{3}\right ) ^{n}+\frac{1}{3}\left ( \frac{2}{3}\right ) ^{n}\hspace{20pt}n\geq 0 \] The solution is stable since both terms go to zero as \(n\rightarrow \infty \)
This is another way to solve problem 6 above. Solve the one sided difference equation \(y\left ( n\right ) -y\left ( n-1\right ) +\frac{2}{9}y\left ( n-2\right ) =x\left ( n\right ) -x\left ( n-1\right ) \) for \(n\geq 0\) where the input is given by \(\delta \left ( n\right ) \) and the IC are given by \(y\left ( -1\right ) =1,y\left ( -2\right ) =0\)
Solution
Since the input is \(\delta \left ( n\right ) \), the difference equation is\[ y\left ( n\right ) -y\left ( n-1\right ) +\frac{2}{9}y\left ( n-2\right ) =\delta \left ( n\right ) -\delta \left ( n-1\right ) \] The homogenous solution is\[ y_{h}\left ( n\right ) -y_{h}\left ( n-1\right ) +\frac{2}{9}y_{h}\left ( n-2\right ) =0 \] Hence the characteristic equation is\begin{align*} z^{2}-z+\frac{2}{9} & =0\\ \left ( z-\frac{2}{3}\right ) \left ( z-\frac{1}{3}\right ) & =0 \end{align*}
Therefore \[ y_{h}\left ( n\right ) =c_{1}\left ( \frac{2}{3}\right ) ^{n}+c_{2}\left ( \frac{1}{3}\right ) ^{n}\ \ \ \ \ \ \ \ \ \ \ n\geq 0 \] Since the input \(x\left ( n\right ) \) is an impulse and is zero for \(n>0\), the particular solution \(y_{p}=0\). Hence the general solution is\begin{equation} y\left ( n\right ) =c_{1}\left ( \frac{2}{3}\right ) ^{n}+c_{2}\left ( \frac{1}{3}\right ) ^{n} \hspace{20pt} n\geq 0 \tag{1} \end{equation} Now we need to find \(c_{1}\) and \(c_{2}\). Lets find \(y\left ( 0\right ) \) and \(y\left ( 1\right ) \) to help do that. From the difference equation, we have for \(n=0\)\begin{align*} y\left ( 0\right ) -y\left ( -1\right ) +\frac{2}{9}y\left ( -2\right ) & =\delta \left ( 0\right ) -\delta \left ( -1\right ) \\ y\left ( 0\right ) & =1-\frac{2}{9}\left ( 0\right ) +1\\ & =2 \end{align*}
for \(n=1\)\begin{align*} y\left ( 1\right ) -y\left ( 0\right ) +\frac{2}{9}y\left ( -1\right ) & =\delta \left ( 1\right ) -\delta \left ( 0\right ) \\ & =\frac{7}{9} \end{align*}
Hence (1) now can be evaluated at \(n=0\) and \(n=1\) and we obtain 2 equations for \(c_{1}\) and \(c_{2}\) and they are\begin{align*} y\left ( 0\right ) & =2=c_{1}+c_{2}\ \\ y\left ( 1\right ) & =\frac{7}{9}=c_{1}\left ( \frac{2}{3}\right ) +c_{2}\left ( \frac{1}{3}\right ) \end{align*}
Solving we obtain \(c_{1}=\frac{1}{3}\) and \(c_{2}=\frac{5}{3}\), hence the solution is\[ y\left ( n\right ) =\frac{1}{3}\left ( \frac{2}{3}\right ) ^{n}+\frac{5}{3}\left ( \frac{1}{3}\right ) ^{n}\ \ \ \ \ \ \ \ \ \ \ n\geq 0 \] Which is the same solution we obtained using the Z transform method.
Find the sequence which has the Z transform \(X\left ( z\right ) =\frac{1}{\left ( 1-z^{-1}\right ) \left ( 1-\frac{1}{2}z^{-1}\right ) }\)
solution
Since the Z transform is not unique without being given its ROC, we first need to determine the valid ROC’s, and for each ROC, determine the corresponding inverse.
Poles are at \(z=1\) and \(z=-\frac{1}{2}\) and the zero is at \(z=0\).
The ROC for a causal system, extends from outside the outermost pole to infinity. Hence for a causal system, the ROC is \(\left \vert z\right \vert >1\). Notice that this system is not stable if it is causal, since the ROC did not include the unit circle, i.e. \(\left \vert z\right \vert =1\).
For an anti causal system, the ROC is the region inside the inner most pole. Hence the ROC is \(\left \vert z\right \vert <\frac{1}{2}\). Notice that this system is not stable if it is anti-causal as well since the ROC does not include the unit circle.
Now we solve the problem.
case 1: ROC is \(\left \vert z\right \vert >1\), i.e. causal system:\[ X\left ( z\right ) =\frac{1}{\left ( 1-z^{-1}\right ) \left ( 1-\frac{1}{2}z^{-1}\right ) }=\frac{A}{\left ( 1-z^{-1}\right ) }+\frac{B}{\left ( 1-\frac{1}{2}z^{-1}\right ) }\] Hence\[ A=\lim _{z^{-1}\rightarrow 1}\frac{1}{\left ( 1-\frac{1}{2}z^{-1}\right ) }=\frac{1}{\left ( 1-\frac{1}{2}\right ) }=2 \] And\[ B=\lim _{z^{-1}\rightarrow 2}\frac{1}{\left ( 1-z^{-1}\right ) }=\frac{1}{\left ( 1-2\right ) }=-1 \] Hence\[ X\left ( z\right ) =\frac{2}{\left ( 1-z^{-1}\right ) }-\frac{1}{\left ( 1-\frac{1}{2}z^{-1}\right ) }\] Therefore\[ y\left ( n\right ) =2u\left ( n\right ) -\left ( \frac{1}{2}\right ) ^{n}u\left ( n\right ) \] case 2: ROC \(\left \vert z\right \vert <\frac{1}{2}\), i.e. anti causal\[ y\left ( n\right ) =-2u\left ( -n-1\right ) +\left ( \frac{1}{2}\right ) ^{n}u\left ( -n-1\right ) \] In both cases, the solution is unstable.
proof that if \(H\left ( z\right ) \) is the transfer function of a stable system then \(\left \vert H\left ( e^{j\omega }\right ) \right \vert <\infty \) for all \(0\leq \omega \leq 2\pi \)
Solution
\(H\left ( z\right ) \) is the Z transform of the impulse response \(h\left ( n\right ) \). Hence\[ H\left ( z\right ) ={\displaystyle \sum \limits _{-\infty }^{\infty }} h\left ( n\right ) z^{-n}\] Let \(z=e^{j\omega }\) \[ H\left ( e^{j\omega }\right ) ={\displaystyle \sum \limits _{-\infty }^{\infty }} h\left ( n\right ) e^{-j\omega n}\] Take the magnitude of both sides\[ \left \vert H\left ( e^{j\omega }\right ) \right \vert =\left \vert{\displaystyle \sum \limits _{-\infty }^{\infty }} h\left ( n\right ) e^{-j\omega n}\right \vert \] But \(\left \vert{\displaystyle \sum \limits _{-\infty }^{\infty }} h\left ( n\right ) e^{-j\omega n}\right \vert \leq{\displaystyle \sum \limits _{-\infty }^{\infty }} \left \vert h\left ( n\right ) e^{-j\omega n}\right \vert \), so the above becomes\begin{align*} \left \vert H\left ( e^{j\omega }\right ) \right \vert & \leq{\displaystyle \sum \limits _{-\infty }^{\infty }} \left \vert h\left ( n\right ) e^{-j\omega n}\right \vert \\ & ={\displaystyle \sum \limits _{-\infty }^{\infty }} \left \vert h\left ( n\right ) \right \vert \left \vert e^{-j\omega n}\right \vert \end{align*}
But \(\left \vert e^{-j\omega n}\right \vert =1\) hence \begin{equation} \left \vert H\left ( e^{j\omega }\right ) \right \vert \leq{\displaystyle \sum \limits _{-\infty }^{\infty }} \left \vert h\left ( n\right ) \right \vert \tag{1} \end{equation} But we are told that this is a stable system, hence by definition of stable system\[{\displaystyle \sum \limits _{-\infty }^{\infty }} h\left ( n\right ) <\infty \] or\begin{align} \left \vert{\displaystyle \sum \limits _{-\infty }^{\infty }} h\left ( n\right ) \right \vert & <\infty \nonumber \\{\displaystyle \sum \limits _{-\infty }^{\infty }} \left \vert h\left ( n\right ) \right \vert & <\infty \tag{2} \end{align}
From (1) and (2) we obtain\[ \left \vert H\left ( e^{j\omega }\right ) \right \vert <\infty \] But \(H\left ( e^{j\omega }\right ) \) is periodic function in \(\omega \) of period \(2\pi \). Hence we only need to consider one period, say \(\left [ 0,2\pi \right ] \,\) QED