4.17 How to solve wave equation using leapfrog method?
Solve \(u_{tt}=c^2 u_{xx}\) for \( 0\geq x \leq 1\) with initial data defined as \(f(x)=\sin \left (2 \pi \frac {x - 0.2}{0.4}\right )\) over \(0.2 \geq x \leq 0.6\) and fixed at both ends.
Mathematica
SetDirectory[NotebookDirectory[]]; Dynamic[p] nPoints=100; speed=351; f1[x_]:= Piecewise[{{Sin[2 Pi (x-0.2)/0.4],0.2<=x<=0.6},{0,True}}]; coord = Table[j h,{j,0,nPoints-1}]; ic = f1[#]&/@ coord; h = 1/(nPoints-1); delT = h/speed; nSteps=1000; end = -1; uNow = ic; uLast = uNow; uNext = uNow; Do[ Which[ n==1, uNext[[2;;end-1]]=(1/2)(uNow[[1;;end-2]]+uNow[[3;;end]]); uLast=uNow; uNow=uNext, n>2, uNext[[2;;(end-1)]]=uNow[[1;;(end-2)]]+uNow[[3;;end]]-uLast[[2;;(end-1)]]; uLast=uNow; uNow=uNext ]; (*Pause[.02];*) p=Grid[{ {Row[{"time",Spacer[5],N[n*delT],Spacer[5],"step number",Spacer[2],n}]}, {ListLinePlot[Transpose[{coord,uNow}],PlotRange->{{-.1,1.1},{-1,1}}, ImageSize->400,GridLines->Automatic,GridLinesStyle->LightGray],SpanFromLeft} },Alignment->Center ], {n,1,nSteps}]; Export["images/mma_100.pdf",p]
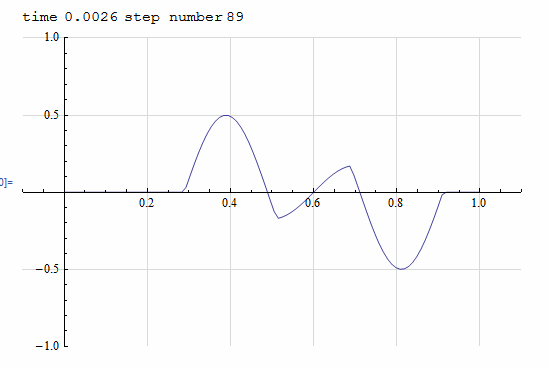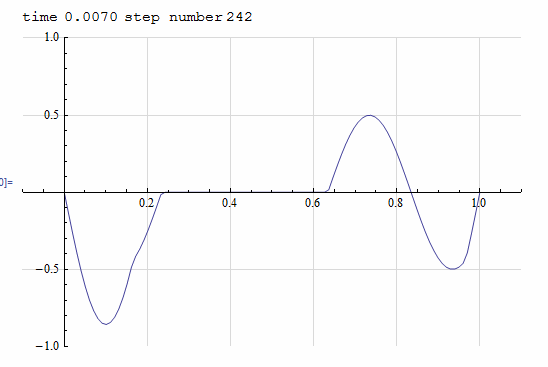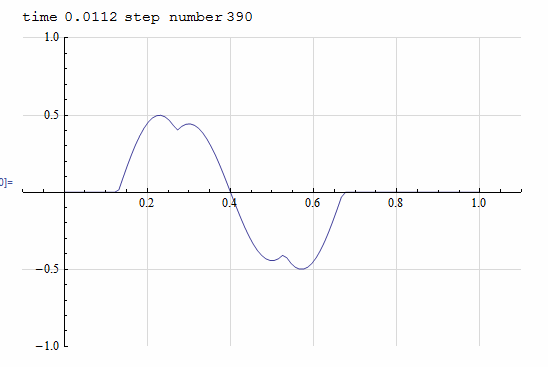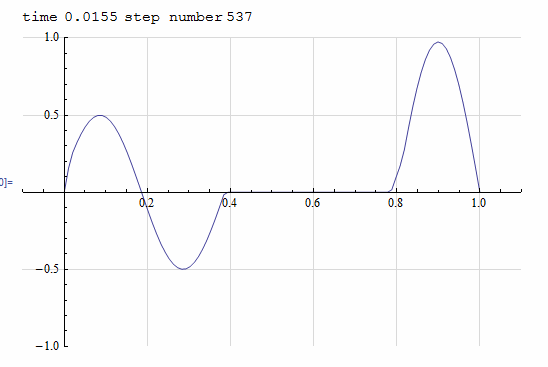
Matlab
%Nasser M. Abbasi July 8, 2014 %solve u_tt = wave_speed * u_xx using leap frog % 0<x<1 % initial data is f(x) % initial speed = 0; % fixed at x=0 and x=1 close all; nPoints = 100; speed = 351; f = @(x) sin(2*pi*(x-0.2)/0.4).*(x>0.2&x<=0.6) coord = linspace(0,1,nPoints); ic = f(coord); h = 1/(nPoints-1); delT = h/speed; last = ic; now = last; next = now; nSteps = 500; for n=1:nSteps if n==1 next(2:end-1) = 1/2*(now(1:end-2)+now(3:end)); last = now; now = next; else next(2:end-1) = now(1:end-2)+now(3:end)-last(2:end-1); last = now; now = next; end plot(now,'r'); xlim([0 nPoints]); ylim([-1 1]); grid; pause(.1); drawnow; end print(gcf, '-dpdf', '-r600', 'images/matlab_100');
Ada
with Ada.Text_IO; use Ada.Text_IO; with Ada.Float_Text_IO; use Ada.Float_Text_IO; with Ada.Integer_Text_IO; use Ada.Integer_Text_IO; with Ada.Numerics; use Ada.Numerics; with Ada.Numerics.Elementary_Functions; use Ada.Numerics.Elementary_Functions; procedure foo is nPoints : constant Integer := 100; type grid_type is array (1 .. nPoints) of Float; Output : File_Type; nSteps : constant Integer := 500; speed : constant Float := 351.0; coord : array (1 .. nPoints) of Float; h : constant Float := 1.0 / (Float (nPoints) - 1.0); delT : constant Float := h / speed; last : grid_type := (others => 0.0); now : grid_type := last; next : grid_type := last; -- output one snapshot to file to plot later procedure put_rec (rec : in grid_type) is begin for i in rec'Range loop Put (Output, rec (i)); Put (Output,' '); end loop; end put_rec; -- define function of initial data function f (x : Float) return Float is begin if (x > 0.2 and x <= 0.6) then return Sin (2.0 * Pi * (x - 0.2) / 0.4); else return 0.0; end if; end f; begin Create (File => Output, Mode => Out_File, Name => "output2.txt"); for i in 1 .. nPoints loop coord (i) := Float (i - 1) * h; last (i) := f (coord (i)); end loop; now := last; next := now; put_rec (now); New_Line (File => Output); for i in 1 .. nSteps loop if i = 1 then for j in 2 .. nPoints - 1 loop next (j) := (1.0 / 2.0) * (now (j - 1) + now (j + 1)); end loop; last := now; now := next; put_rec (now); New_Line (File => Output); else for j in 2 .. nPoints - 1 loop next (j) := now (j - 1) + now (j + 1) - last (j); end loop; last := now; now := next; put_rec (now); if i < nSteps then New_Line (File => Output); end if; end if; end loop; Close (Output); end foo;The GPR file to build the above is
project One is for Main use ("foo.adb"); for Source_Files use ("foo.adb"); package Builder is for Executable_Suffix use ".exe"; end Builder; package Compiler is for Default_Switches ("ada") use ("-g", "-gnata", "-gnato", "-fstack-check", "-gnatE", "-fcallgraph-info=su,da"); end Compiler; end One;
The animation for Ada was done by reading the output and using the plot command in Matlab to show the result.
close all; A= dlmread('output2.txt'); [nRow,nCol]=size(A); for i=1:2:nRow plot(A(i,:)) ylim([-1 1]); grid; pause(.1); drawnow; end