We need to solve \(2\left ( \frac{\partial ^{2}u}{\partial x^{2}}+\frac{\partial ^{2}u}{\partial y^{2}}\right ) -\left ( \frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}\right ) -5u=5\) on the unit square. The discretized algebraic equation resulting from approximating this PDE using standard 5 point Laplacian and centered difference for the first derivatives is given by\begin{align*} \frac{\partial ^{2}u}{\partial x^{2}}+\frac{\partial ^{2}u}{\partial y^{2}} & =\frac{1}{h^{2}}\left ( U_{i-1,j}+U_{i+1,j}+U_{i,j-1}+U_{i,j+1}-4U_{i,j}\right ) \\ \frac{\partial u}{\partial x} & =\frac{1}{2h}\left ( U_{i+1,j}-U_{i-1,j}\right ) \\ \frac{\partial u}{\partial y} & =\frac{1}{2h}\left ( U_{i,j+1}-U_{i,j-1}\right ) \end{align*}
which has local truncation error \(O\left ( h^{2}\right ) \). Therefore the PDE becomes
\begin{align*} 2\left ( \frac{1}{h^{2}}\left ( U_{i-1,j}+U_{i+1,j}+U_{i,j-1}+U_{i,j+1}-4U_{i,j}\right ) \right ) -\frac{1}{2h}\left ( U_{i+1,j}-U_{i-1,j}+U_{i,j+1}-U_{i,j-1}\right ) -5U_{i,j} & =-5\\ U_{i-1,j}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{i+1,j}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{i,j-1}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{i,j+1}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{i,j}\left ( \frac{-8}{h^{2}}-5\right ) & =-5 \end{align*}
The numbering system used for the grid is the following. The indices for the unknown \(U_{i,j}\) are numbered row wise, left to right, bottom to top. This follows the standard Cartesian coordinates system.

Lower case \(n\) is used to indicate the number of unknowns along one dimension, and upper case \(N\) is used to indicate the total number of unknowns. For example, if we use a grid with 5 points on each side, we obtain

In the diagram above, \(n=3\) is the number of unknowns on each one row or each column, and since there are \(3\) internal rows, there will be \(9\) unknowns in total, all are located on internal grid points. There are a total of \(25\) grid points, \(16\) of which are on the boundaries (given as zero) and \(9\) are internal (which we need to solve for).
We will derive the first few rows of the \(A\) matrix to see the structure. For \(i=1,j=1\)
\[ U_{0,1}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{2,1}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{1,0}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{1,2}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{1,1}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
For \(i=2,j=1\)
\[ U_{1,1}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{3,1}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{2,0}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{2,2}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{2,1}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
For \(i=3,j=1\)
\[ U_{2,1}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{4,1}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{3,0}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{3,2}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{3,1}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
The above completes one row (it is the bottom row in the grid) but it goes as the first row in the \(A\) matrix. Since boundary conditions are zero, then we can eliminate \(U_{0,1},U_{4,1},U_{1,0},U_{2,0},U_{3},_{0}\) from the first row. Hence the above becomes
For \(i=1,j=1\)
\[ U_{2,1}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{1,2}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{1,1}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
For \(i=2,j=1\)
\[ U_{1,1}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{3,1}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{2,2}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{2,1}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
For \(i=3,j=1\)
\[ U_{2,1}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{3,2}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{3,1}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
Looking at the second row in the grid (the second row from the bottom up), we find
For \(i=1,J=2\)
\[ U_{0,2}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{2,2}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{1,1}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{1,3}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{1,2}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
For \(i=2,j=2\)
\[ U_{1,2}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{3,2}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{2,1}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{2,3}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{2,2}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
For \(i=3,j=2\)
\[ U_{2,2}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{4,2}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{3,1}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{3,3}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{3,2}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
Removing boundary conditions entries the above becomes
For \(i=1,J=2\)
\[ U_{2,2}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{1,1}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{1,3}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{1,2}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
For \(i=2,j=2\)
\[ U_{1,2}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{3,2}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{2,1}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{2,3}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{2,2}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
For \(i=3,j=2\)
\[ U_{2,2}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{3,1}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{3,3}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{3,2}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
And finally for the third row from the bottom up, (this will be the last row in the \(A\) matrix) we have
For \(i=1,J=3\)
\[ U_{0,3}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{2,3}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{1,2}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{1,4}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{1,3}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
For \(i=2,j=3\)
\[ U_{1,3}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{3,3}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{2,2}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{2,4}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{2,3}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
For \(i=3,j=3\)
\[ U_{2,3}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{4,3}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{3,2}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{3,4}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{3,3}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
Removing boundary conditions entries the above becomes
For \(i=1,J=3\)
\[ U_{2,3}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{1,2}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{1,3}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
For \(i=2,j=3\)
\[ U_{1,3}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{3,3}\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) +U_{2,2}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{2,3}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
For \(i=3,j=3\)
\[ U_{2,3}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{3,2}\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) +U_{3,3}\left ( \frac{-8}{h^{2}}-5\right ) =-5 \]
Therefor the \(Au=f\) structure is the following
\[\begin{pmatrix} \left ( \frac{-8}{h^{2}}-5\right ) & \left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) & 0 & \left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) & 0 & 0 & 0 & 0 & 0\\ \left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) & \left ( \frac{-8}{h^{2}}-5\right ) & \left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) & 0 & \left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) & 0 & 0 & 0 & 0\\ 0 & \left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) & \left ( \frac{-8}{h^{2}}-5\right ) & 0 & 0 & \left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) & 0 & 0 & 0\\ \left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) & 0 & 0 & \left ( \frac{-8}{h^{2}}-5\right ) & \left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) & 0 & \left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) & 0 & 0\\ 0 & \left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) & 0 & \left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) & \left ( \frac{-8}{h^{2}}-5\right ) & \left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) & 0 & \left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) & 0\\ 0 & 0 & \left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) & 0 & \left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) & \left ( \frac{-8}{h^{2}}-5\right ) & 0 & 0 & \left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) \\ 0 & 0 & 0 & \left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) & 0 & 0 & \left ( \frac{-8}{h^{2}}-5\right ) & \left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) & 0\\ 0 & 0 & 0 & 0 & \left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) & 0 & \left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) & \left ( \frac{-8}{h^{2}}-5\right ) & \left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) \\ 0 & 0 & 0 & 0 & 0 & \left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) & 0 & \left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) & \left ( \frac{-8}{h^{2}}-5\right ) \end{pmatrix}\begin{pmatrix} U_{1,1}\\ U_{2,1}\\ U_{3,1}\\ U_{1,2}\\ U_{2,2}\\ U_{3,2}\\ U_{1,3}\\ U_{2,3}\\ U_{3,3}\end{pmatrix} =\begin{pmatrix} -5\\ -5\\ -5\\ -5\\ -5\\ -5\\ -5\\ -5\\ -5 \end{pmatrix} \]
To simplify, let \(c_{1}=\left ( \frac{-8}{h^{2}}-5\right ) ,c_{2}=\left ( \frac{2}{h^{2}}-\frac{1}{2h}\right ) ,c_{3}=\left ( \frac{2}{h^{2}}+\frac{1}{2h}\right ) \)) since these repeat everywhere.
\[ \boxed{ \begin{pmatrix} c_{1} & c_{2} & 0 & c_{2} & 0 & 0 & 0 & 0 & 0\\ c_{3} & c_{1} & c_{2} & 0 & c_{2} & 0 & 0 & 0 & 0\\ 0 & c_{3} & c_{1} & 0 & 0 & c_{2} & 0 & 0 & 0\\ c_{3} & 0 & 0 & c_{1} & c_{2} & 0 & c_{2} & 0 & 0\\ 0 & c_{3} & 0 & c_{3} & c_{1} & c_{2} & 0 & c_{2} & 0\\ 0 & 0 & c_{3} & 0 & c_{3} & c_{1} & 0 & 0 & c_{2}\\ 0 & 0 & 0 & c_{3} & 0 & 0 & c_{1} & c_{2} & 0\\ 0 & 0 & 0 & 0 & c_{3} & 0 & c_{3} & c_{1} & c_{2}\\ 0 & 0 & 0 & 0 & 0 & c_{3} & 0 & c_{3} & c_{1}\end{pmatrix}\begin{pmatrix} U_{1,1}\\ U_{2,1}\\ U_{3,1}\\ U_{1,2}\\ U_{2,2}\\ U_{3,2}\\ U_{1,3}\\ U_{2,3}\\ U_{3,3}\end{pmatrix} =\begin{pmatrix} -5\\ -5\\ -5\\ -5\\ -5\\ -5\\ -5\\ -5\\ -5 \end{pmatrix} } \]
So now we see the structure of \(Au=f\). For the number of unknowns being \(n\) in one row, we have the following layout

The program nma_EMA_471_HW6_problem_1.m solves this \(Au=f\) using the direct method and plots the solution. Maximum value found was
\[ \boxed{u_{\max }=0.1609} \]
Here is plot of the solution

On the left edge we have (where \(i=0\)) we have

And on the bottom edge where \(j=0\) we have

Using the above relations, then at node \(i=0\),
\[ \frac{\partial ^{2}T}{\partial x^{2}}=\frac{T_{1,j}-2T_{0,j}+T_{-1,j}}{h^{2}}\]
Using the relation we found earlier, which said that \(T_{-1,j}=T_{1,j}\), the above becomes
\[ \frac{\partial ^{2}T}{\partial x^{2}}=\frac{2T_{1,j}-2T_{0,j}}{h^{2}}\]
Therefore, the differential equation at \(i=0\) and for all \(j\) becomes
\begin{align} \nabla ^{2}T-20T & =-200\nonumber \\ \frac{\partial ^{2}T}{\partial x^{2}}+\frac{\partial ^{2}T}{\partial y^{2}}-20T & =-200\nonumber \\ \frac{2T_{1,j}-2T_{0,j}}{h^{2}}+\frac{T_{0,j+1}-2T_{0,j}+T_{0,j-1}}{h^{2}}-20T_{0,j} & =-200 \tag{1} \end{align}
The above is what we will use on the left edge, for \(j=1\cdots N\) where \(N\) is the number of internal nodes. We now find the PDE on the lower edge in similar way. On the bottom edge, where \(j=0\), we have
\[ \frac{\partial ^{2}T}{\partial y^{2}}=\frac{T_{i,1}-2T_{i,0}+T_{i,-1}}{h^{2}}\]
Using the relation we found earlier, which said that \(T_{i,-1}=T_{i,1}\), then the above becomes
\[ \frac{\partial ^{2}T}{\partial y^{2}}=\frac{2T_{i,1}-2T_{i,0}}{h^{2}}\]
Therefore, the differential equation at \(j=0\) and for all \(i\) becomes
\begin{align} \frac{\partial ^{2}T}{\partial x^{2}}+\frac{\partial ^{2}T}{\partial y^{2}}-20T & =-200\nonumber \\ \frac{T_{i+1,0}-2T_{i,0}+T_{i-1,0}}{h^{2}}+\frac{2T_{i,1}-2T_{i,0}}{h^{2}}-20T_{i,0} & =-200 \tag{2} \end{align}
The above is what we will use on the bottom edge, for \(i=1\cdots N\) where \(N\) is the number of internal nodes. Now that we found the PDE on the left and on the right edge, we write the PDE on the internal nodes, which is the standard form
\begin{align} \frac{\partial ^{2}T}{\partial x^{2}}+\frac{\partial ^{2}T}{\partial y^{2}}-20T & =-200\nonumber \\ \frac{T_{i+1,j}-2T_{i,j}+T_{i-1,j}}{h^{2}}+\frac{T_{i,j+1}-2T_{i,j}+T_{i,j-1}}{h^{2}}-20T_{i,j} & =-200 \tag{3} \end{align}
Using (1,2,3) equations, we now find the \(Ax=f\) form. Let us assume that \(N=3\), so our grid is the following

For \(i=0,j=0\), this is special node. We can either use the condition for the left edge to handle it, or the condition for the bottom edge, or use the average of the adjacent nodes. Let us use the bottom edge condition for it. Hence at this node the PDE is from (2)
\begin{align} \frac{T_{1,0}-2T_{0,0}+T_{-1,0}}{h^{2}}+\frac{2T_{0,1}-2T_{0,0}}{h^{2}}-20T_{0,0} & =-200\nonumber \\ \frac{2T_{1,0}-2T_{0,0}}{h^{2}}+\frac{2T_{0,1}-2T_{0,0}}{h^{2}}-20T_{0,0} & =-200\nonumber \\ 2T_{1,0}-2T_{0,0}+2T_{0,1}-2T_{0,0}-20h^{2}T_{0,0} & =-200h^{2}\nonumber \\ 2T_{1,0}+T_{0,0}\left ( -4-20h^{2}\right ) +2T_{0,1} & =-200h^{2} \tag{0,0} \end{align}
For \(i=1,j=0\), from (2)
\begin{align} \frac{T_{2,0}-2T_{1,0}+T_{0,0}}{h^{2}}+\frac{2T_{1,1}-2T_{1,0}}{h^{2}}-20T_{1,0} & =-200\nonumber \\ T_{2,0}+T_{1,0}\left ( -4-20h^{2}\right ) +T_{0,0}+2T_{1,1} & =-200h^{2} \tag{1,0} \end{align}
And for \(i=2,j=0\)
\begin{align} \frac{T_{3,0}-2T_{2,0}+T_{1,0}}{h^{2}}+\frac{2T_{2,1}-2T_{2,0}}{h^{2}}-20T_{2,0} & =-200\nonumber \\ T_{3,0}-4T_{2,0}+T_{1,0}+2T_{2,1}-20h^{2}T_{2,0} & =-200h^{2}\nonumber \\ T_{3,0}+T_{2,0}\left ( -4-20h^{2}\right ) +T_{1,0}+2T_{2,1} & =-200h^{2} \tag{2,0} \end{align}
And for \(i=3,j=0\)
\begin{align*} \frac{T_{4,0}-2T_{3,0}+T_{2,0}}{h^{2}}+\frac{2T_{3,1}-2T_{3,0}}{h^{2}}-20T_{3,0} & =-200\\ T_{4,0}-4T_{3,0}+T_{2,0}+2T_{3,1}-20h^{2}T_{3,0} & =-200h^{2}\\ T_{4,0}+T_{3,0}\left ( -4-20h^{2}\right ) +T_{2,0}+2T_{3,1} & =-200h^{2} \end{align*}
But \(T_{4,0}\) is know, since it is on the right edge and is zero there. Hence the above becomes
\begin{equation} T_{3,0}\left ( -4-40h\right ) +T_{2,0}+2T_{3,1}=-200h^{2} \tag{3,0} \end{equation}
We now move to the second grid line from the bottom. On the first node, which is \(i=0,j=1\), we use the left edge PDE, which is (1). Hence
\begin{align} \frac{2T_{1,1}-2T_{0,1}}{h^{2}}+\frac{T_{0,2}-2T_{0,1}+T_{0,0}}{h^{2}}-20T_{0,1} & =-200\nonumber \\ 2T_{1,1}-4T_{0,1}+T_{0,2}+T_{0,0}-20h^{2}T_{0,1} & =-200h^{2}\nonumber \\ 2T_{1,1}+T_{0,1}\left ( -4-20h^{2}\right ) +T_{0,2}+T_{0,0} & =-200h^{2} \tag{0,1} \end{align}
And for \(i=1,j=1,\) this is an internal node, so we use (3)
\begin{align} \frac{T_{2,1}-2T_{1,1}+T_{0,1}}{h^{2}}+\frac{T_{1,2}-2T_{1,1}+T_{1,0}}{h^{2}}-20T_{1,1} & =-200\nonumber \\ T_{2,1}-4T_{1,1}+T_{0,1}+T_{1,2}+T_{1,0}-20h^{2}T_{1,1} & =-200h^{2}\nonumber \\ T_{2,1}+T_{1,1}\left ( -4-20h^{2}\right ) +T_{0,1}+T_{1,2}+T_{1,0} & =-200h^{2} \tag{1,1} \end{align}
And for \(i=2,j=1,\) this is an internal node, so we use (3)
\begin{align} \frac{T_{3,1}-2T_{2,1}+T_{1,1}}{h^{2}}+\frac{T_{2,2}-2T_{2,1}+T_{2,0}}{h^{2}}-20T_{2,1} & =-200\nonumber \\ T_{3,1}+T_{2,1}\left ( -4-20h^{2}\right ) +T_{1,1}+T_{2,2}+T_{2,0} & =-200h^{2} \tag{2,1} \end{align}
And for \(i=3,j=1,\) this is an internal node, so we use (3) and set \(T_{4,1}=0\) since known
\begin{align} \frac{T_{4,1}-2T_{3,1}+T_{2,1}}{h^{2}}+\frac{T_{3,2}-2T_{3,1}+T_{3,0}}{h^{2}}-20T_{3,1} & =-200\nonumber \\ T_{3,1}\left ( -4-20h^{2}\right ) +T_{2,1}+T_{3,2}+T_{3,0} & =-200h^{2} \tag{3,1} \end{align}
For node \(i=4,j=1\), this is a known value for \(T\) there, so we skip it. Going to the next grid row above, for \(i=0,j=2\), this is a left edge node, so we use (1)
\begin{align} \frac{2T_{1,2}-2T_{0,2}}{h^{2}}+\frac{T_{0,3}-2T_{0,2}+T_{0,1}}{h^{2}}-20T_{0,2} & =-200\nonumber \\ 2T_{1,2}+T_{0,2}\left ( -4-20h^{2}\right ) +T_{0,3}+T_{0,1} & =-200h^{2} \tag{0,2} \end{align}
For \(i=1,j=2\), this is an internal node, so we use (3)
\begin{align} \frac{T_{2,2}-2T_{1,2}+T_{0,2}}{h^{2}}+\frac{T_{1,3}-2T_{1,2}+T_{1,1}}{h^{2}}-20T_{1,2} & =-200\nonumber \\ T_{2,2}+T_{1,2}\left ( -4-20h^{2}\right ) +T_{0,2}+T_{1,3}+T_{1,1} & =-200h^{2} \tag{1,2} \end{align}
For \(i=2,j=2,\) this is an internal node, so we use (3)
\begin{align} \frac{T_{3,2}-2T_{2,2}+T_{1,2}}{h^{2}}+\frac{T_{2,3}-2T_{2,2}+T_{2,1}}{h^{2}}-20T_{2,2} & =-200\nonumber \\ T_{3,2}+T_{2,2}\left ( -4-20h^{2}\right ) +T_{1,2}+T_{2,3}+T_{2,1} & =-200h^{2} \tag{2,2} \end{align}
And for \(i=3,j=2\), this is an internal node, so we use (3) and set \(T_{4,2}=0\) since known
\begin{align} \frac{T_{4,2}-2T_{3,2}+T_{2,2}}{h^{2}}+\frac{T_{3,3}-2T_{3,2}+T_{3,1}}{h^{2}}-20T_{3,2} & =-200\nonumber \\ T_{3,2}\left ( -4-20h^{2}\right ) +T_{2,2}+T_{3,3}+T_{3,1} & =-200h^{2} \tag{3,2} \end{align}
For node \(i=4,j=2\), this is a known value for \(T\) there, so we skip it. Going to the next grid row above, for \(i=0,j=3\), this is a left edge node, so we use (1)
\begin{align*} \frac{2T_{1,3}-2T_{0,3}}{h^{2}}+\frac{T_{0,4}-2T_{0,3}+T_{0,2}}{h^{2}}-20T_{0,3} & =-200\\ 2T_{1,3}+T_{0,3}\left ( -4-20h^{2}\right ) +T_{0,4}+T_{0,2} & =-200h^{2} \end{align*}
But \(T_{0,4}\) is on the top edge, which is known and is zero, therefore the above is
\begin{equation} 2T_{1,3}+T_{0,3}\left ( -4-20h^{2}\right ) +T_{0,2}=-200h^{2} \tag{0,3} \end{equation}
For node \(i=1,j=3\), this is an internal node, so we use (3)
\begin{align*} \frac{T_{2,3}-2T_{1,3}+T_{0,3}}{h^{2}}+\frac{T_{1,4}-2T_{1,3}+T_{1,2}}{h^{2}}-20T_{1,3} & =-200\\ T_{2,3}+T_{1,3}\left ( -4-20h^{2}\right ) +T_{0,3}+T_{1,4}+T_{1,2} & =-200h^{2} \end{align*}
But \(T_{1,4}\) is on the top edge, which is known and is zero, therefore the above is
\begin{equation} T_{2,3}+T_{1,3}\left ( -4-20h^{2}\right ) +T_{0,3}+T_{1,2}=-200h^{2} \tag{1,3} \end{equation}
And on node \(i=2,j=3\), this is an internal node, so we use (3)
\begin{align*} \frac{T_{3,3}-2T_{2,3}+T_{1,3}}{h^{2}}+\frac{T_{2,4}-2T_{2,3}+T_{2,2}}{h^{2}}-20T_{2,3} & =-200\\ T_{3,3}+T_{2,3}\left ( -4-20h^{2}\right ) +T_{1,3}+T_{2,4}+T_{2,2} & =-200h^{2} \end{align*}
But \(T_{2,4}\) is on the top edge, which is known and is zero, therefore the above is
\begin{equation} T_{3,3}+T_{2,3}\left ( -4-20h^{2}\right ) +T_{1,3}+T_{2,2}=-200h^{2} \tag{2,3} \end{equation}
Finally, for node \(i=3,j=3\)
\begin{align*} \frac{T_{4,3}-2T_{3,3}+T_{2,3}}{h^{2}}+\frac{T_{3,4}-2T_{3,3}+T_{3,2}}{h^{2}}-20T_{3,3} & =-200\\ T_{4,3}+T_{3,3}\left ( -4-20h^{2}\right ) +T_{2,3}+T_{3,4}+T_{3,2} & =-200h^{2} \end{align*}
But \(T_{3,4}\) and \(T_{4,3}\) are known and is zero, therefore the above is
\begin{equation} T_{3,3}\left ( -4-20h^{2}\right ) +T_{2,3}+T_{3,2}=-200h^{2} \tag{3,3} \end{equation}
Now we able to see the form of the matrix \(A\) by writing the equations for this small grid. There are \(16\) unknowns. Let \(\left ( -4-20h^{2}\right ) =\alpha \) then
\[\begin{array} [c]{c}\text{{\small bottom edge}}\\ \text{{\small bottom edge}}\\ \text{{\small bottom edge}}\\ \text{{\small bottom edge}}\\ \text{{\small left edge}}\\ \text{{\small internal nodes}}\\ \text{{\small internal nodes}}\\ \text{{\small internal nodes}}\\ \text{{\small left edge}}\\ \text{{\small internal nodes}}\\ \text{{\small internal nodes}}\\ \text{{\small internal nodes}}\\ \text{{\small left edge}}\\ \text{{\small row below top edge}}\\ \text{{\small row below top edge}}\\ \text{{\small row below top edge}}\end{array}\begin{bmatrix} \alpha & 2 & 0 & 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 1 & \alpha & 1 & 0 & 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & \alpha & 1 & 0 & 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & \alpha & 0 & 0 & 0 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & \alpha & 2 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 1 & \alpha & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 1 & \alpha & 1 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 1 & \alpha & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & \alpha & 2 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & \alpha & 1 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & \alpha & 1 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & \alpha & 0 & 0 & 0 & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & \alpha & 2 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & \alpha & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & \alpha & 1\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 1 & \alpha \end{bmatrix}\begin{bmatrix} T_{0,0}\\ T_{1,0}\\ T_{2,0}\\ T_{3,0}\\ T_{0,1}\\ T_{1,1}\\ T_{2,1}\\ T_{3,1}\\ T_{0,2}\\ T_{1,2}\\ T_{2,2}\\ T_{3,2}\\ T_{0,3}\\ T_{1,3}\\ T_{2,3}\\ T_{3,3}\end{bmatrix} =\begin{bmatrix} -200h^{2}\\ -200h^{2}\\ -200h^{2}\\ -200h^{2}\\ -200h^{2}\\ -200h^{2}\\ -200h^{2}\\ -200h^{2}\\ -200h^{2}\\ -200h^{2}\\ -200h^{2}\\ -200h^{2}\\ -200h^{2}\\ -200h^{2}\\ -200h^{2}\\ -200h^{2}\end{bmatrix} \]
The above was implemented in the matlab program nma_EMA_471_HW6_problem_2.m. The maximum value of \(T\) found was
\[ 9.577 \]
Here is the 3D plot and a contour plot.

And this is the 3D plot.

I have also solved this in Mathematica, using the finite element solver build into NDSOlve. I also obtained the same result. Here is the contour plot and the 3D plot.


The grid numbering used is the following

The PDE is, for \(0\leq \theta \leq \frac{\pi }{2}\)
\[ \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}}=-200 \]
And for \(\frac{\pi }{2}<\theta \leq \pi \)
\[ \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}}=0 \]
For the nodes with \(\theta =\frac{\pi }{2}\) we will use
\[ \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}}=-100 \]
Using centered difference, and using \(T_{ij}\) to mean \(T_{r_{i},\theta j}\) then the above can be written as
\begin{equation} \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}}=-200 \tag{1} \end{equation}
Where \(i=1\cdots N_{r}\) where \(N_{r}\) is the number of grid points in the radial direction, which is \(3\) in the diagram above. The following diagram shows the boundary conditions to use.

We now find the \(A\) matrix in order to solve the problem using the direct method. We assume \(N_{\theta }=7\) and \(N_{r}=5\) for the purpose of seeing what the \(A\) structure is

For node \(\left ( 1,1\right ) \), this is the special node. which is
\[ T_{1,1}=\frac{0.5T_{2,1}+T_{2,2}+T_{2,3}+\cdots +T_{2,N-1}+0.5T_{2,N_{\theta }}}{N_{\theta }-1}+25\Delta r^{2}\]
Where \(N_{\theta }\) is the number of grid point in the angular direction. For example, in the diagram given above, \(N_{\theta }=7\), hence
\begin{align} T_{1,1}-\frac{0.5T_{2,1}+T_{2,2}+T_{2,3}+T_{2,4}+T_{2,5}+T_{2,6}+0.5T_{2,7}}{6} & =25\Delta r^{2}\nonumber \\ T_{1,1}-\frac{1}{12}T_{2,1}-\frac{1}{6}T_{2,2}-\frac{1}{6}T_{2,3}-\frac{1}{6}T_{2,4}-\frac{1}{6}T_{2,5}-\frac{1}{6}T_{2,6}-\frac{1}{12}T_{2,7} & =25\Delta r^{2}\tag{1,1} \end{align}
For node \(\left ( 2,1\right ) \), this is an insulated node. Hence by introducing an imaginary node as shown above, then on this node, the PDE is
\begin{align*} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =-200\\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =-200\\ \frac{T_{1,1}-2T_{21}+T_{3,1}}{\Delta r^{2}}+\frac{1}{\Delta r}\frac{T_{3,1}-T_{1,1}}{2\Delta r}+\frac{1}{\Delta r^{2}}\frac{T_{2,0}-2T_{2,1}+T_{2,2}}{\Delta \theta ^{2}} & =-200 \end{align*}
But due to insulation, then \(\frac{\partial T}{\partial \theta }=\frac{T_{i,j+1}-T_{i,j-1}}{2\Delta \theta }=0\) which means \(T_{i,j+1}=T_{i,j-1}\), or at this node \(T_{2,0}=T_{2,2}\), hence the above becomes
\[ \frac{T_{1,1}-2T_{21}+T_{3,1}}{\Delta r^{2}}+\frac{1}{\Delta r}\frac{T_{3,1}-T_{1,1}}{2\Delta r}+\frac{1}{\Delta r^{2}}\frac{2T_{2,2}-2T_{2,1}}{\Delta \theta ^{2}}=-200 \]
Collecting terms
\begin{align} T_{1,1}\left ( \frac{1}{\Delta r^{2}}-\frac{1}{2\Delta r^{2}}\right ) +T_{2,1}\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{3,1}\left ( \frac{1}{\Delta r^{2}}+\frac{1}{2\Delta r^{2}}\right ) +T_{2,2}\left ( \frac{2}{\Delta r^{2}\Delta \theta ^{2}}\right ) & =-200\nonumber \\ T_{1,1}\left ( \frac{1}{2\Delta r^{2}}\right ) +T_{2,1}\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{3,1}\left ( \frac{3}{2\Delta r^{2}}\right ) +T_{2,2}\left ( \frac{2}{\Delta r^{2}\Delta \theta ^{2}}\right ) & =-200 \tag{2,1} \end{align}
At node \(\left ( 3,1\right ) \)
\begin{align*} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =-200\\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =-200\\ \frac{T_{2,1}-2T_{3,1}+T_{4,1}}{\Delta r^{2}}+\frac{1}{2\left ( \Delta r\right ) }\frac{T_{4,1}-T_{2,1}}{2\Delta r}+\frac{1}{\left [ 2\left ( \Delta r\right ) \right ] ^{2}}\frac{T_{3,0}-2T_{3,1}+T_{3,2}}{\Delta \theta ^{2}} & =-200 \end{align*}
But due to insulation, then \(\frac{\partial T}{\partial \theta }=\frac{T_{i,j+1}-T_{i,j-1}}{2\Delta \theta }=0\) which means \(T_{i,j+1}=T_{i,j-1}\), or at this node \(T_{3,0}=T_{3,2}\), hence the above becomes
\[ \frac{T_{2,1}-2T_{3,1}+T_{4,1}}{\Delta r^{2}}+\frac{1}{2\left ( \Delta r\right ) }\frac{T_{4,1}-T_{2,1}}{2\Delta r}+\frac{1}{\left [ 2\left ( \Delta r\right ) \right ] ^{2}}\frac{2T_{3,2}-2T_{3,1}}{\Delta \theta ^{2}}=-200 \]
Collecting terms
\begin{align} T_{2,1}\left ( \frac{1}{\Delta r^{2}}-\frac{1}{4\Delta r^{2}}\right ) +T_{3,1}\left ( -\frac{2}{\Delta r^{2}}-\frac{2}{\left [ 2\left ( \Delta r\right ) \right ] ^{2}\Delta \theta ^{2}}\right ) +T_{4,1}\left ( \frac{1}{\Delta r^{2}}+\frac{1}{4\Delta r^{2}}\right ) +T_{3,2}\left ( \frac{2}{\left [ 2\left ( \Delta r\right ) \right ] ^{2}\Delta \theta ^{2}}\right ) & =-200\nonumber \\ T_{2,1}\left ( \frac{3}{4\Delta r^{2}}\right ) +T_{3,1}\left ( -\frac{2}{\Delta r^{2}}-\frac{1}{2\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,1}\left ( \frac{5}{4\Delta r^{2}}\right ) +T_{3,2}\left ( \frac{1}{2\Delta r^{2}\Delta \theta ^{2}}\right ) & =-200 \tag{3,1} \end{align}
At node \(\left ( 4,1\right ) \)
\begin{align*} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =-200\\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =-200\\ \frac{T_{3,1}-2T_{4,1}+T_{5,1}}{\Delta r^{2}}+\frac{1}{3\Delta r}\frac{T_{5,1}-T_{3,1}}{2\Delta r}+\frac{1}{9\Delta r^{2}}\frac{T_{4,0}-2T_{4,1}+T_{4,2}}{\Delta \theta ^{2}} & =-200 \end{align*}
But due to insulation, then \(\frac{\partial T}{\partial \theta }=\frac{T_{i,j+1}-T_{i,j-1}}{2\Delta \theta }=0\) which means \(T_{i,j+1}=T_{i,j-1}\), or at this node \(T_{4,0}=T_{4,2}\), hence the above becomes (and also \(T_{5,1}=0\) since on boundary)
\[ \frac{T_{3,1}-2T_{4,1}}{\Delta r^{2}}+\frac{1}{3\Delta r}\frac{-T_{3,1}}{2\Delta r}+\frac{1}{9\Delta r^{2}}\frac{-2T_{4,1}+2T_{4,2}}{\Delta \theta ^{2}}=-200 \]
Collecting terms
\begin{equation} T_{3,1}\left ( \frac{5}{6\Delta r^{2}}\right ) +T_{4,1}\left ( -\frac{2}{\Delta r^{2}}-\frac{2}{9\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,2}\left ( \frac{2}{9\Delta r^{2}\Delta \theta ^{2}}\right ) =-200 \tag{4,1} \end{equation}
The above completes half of the bottom grid row. Now we move to the next grid at, one \(\Delta \theta \) above.
At node \(\left ( 2,2\right ) \), this is an internal node.
\begin{align*} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =-200\\ \frac{T_{1,2}-2T_{22}+T_{3,2}}{\Delta r^{2}}+\frac{1}{\Delta r}\frac{T_{3,2}-T_{1,2}}{2\Delta r}+\frac{1}{\Delta r^{2}}\frac{T_{2,1}-2T_{22}+T_{2,3}}{\Delta \theta ^{2}} & =-200 \end{align*}
Collecting terms
\[ T_{1,2}\left ( \frac{1}{\Delta r^{2}}-\frac{1}{2\Delta r^{2}}\right ) +T_{22}\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{3,2}\left ( \frac{1}{\Delta r^{2}}+\frac{1}{2\Delta r^{2}}\right ) +T_{2,1}\left ( \frac{1}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{2,3}\left ( \frac{1}{\Delta r^{2}\Delta \theta ^{2}}\right ) =-200 \]
But \(T_{1,2}=T_{1,1}\). This is the same node. Hence the above becomes
\begin{equation} T_{1,1}\left ( \frac{1}{2\Delta r^{2}}\right ) +T_{22}\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{3,2}\left ( \frac{3}{2\Delta r^{2}}\right ) +T_{2,1}\left ( \frac{1}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{2,3}\left ( \frac{1}{\Delta r^{2}\Delta \theta ^{2}}\right ) =-200 \tag{2,2} \end{equation}
At node \(\left ( 3,2\right ) \), this is an internal node
\begin{align} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =-200\nonumber \\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =-200\nonumber \\ \frac{T_{2,2}-2T_{3,2}+T_{4,2}}{\Delta r^{2}}+\frac{1}{2\Delta r}\frac{T_{4,2}-T_{2,2}}{2\Delta r}+\frac{1}{\left [ 2\left ( \Delta r\right ) \right ] ^{2}}\frac{T_{3,1}-2T_{3,2}+T_{3,3}}{\Delta \theta ^{2}} & =-200\nonumber \\ T_{2,2}\left ( \frac{3}{4\Delta r^{2}}\right ) +T_{3,2}\left ( \frac{-2}{\Delta r^{2}}-\frac{1}{2\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,2}\left ( \frac{5}{4\Delta r^{2}}\right ) +T_{3,1}\left ( \frac{1}{4\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{3,3}\left ( \frac{1}{4\Delta r^{2}\Delta \theta ^{2}}\right ) & =-200 \tag{3,2} \end{align}
At node \(\left ( 4,2\right ) ,\)this is an internal node
\begin{align*} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =-200\\ \frac{T_{3,2}-2T_{4,2}+T_{5,2}}{\Delta r^{2}}+\frac{1}{3\Delta r}\frac{T_{5,2}-T_{3,2}}{2\Delta r}+\frac{1}{\left [ 3\left ( \Delta r\right ) \right ] ^{2}}\frac{T_{4,1}-2T_{4,2}+T_{4,3}}{\Delta \theta ^{2}} & =-200 \end{align*}
But \(T_{5,2}=0\) since on boundary, hence
\begin{align} \frac{T_{3,2}-2T_{4,2}}{\Delta r^{2}}+\frac{1}{3\Delta r}\frac{-T_{3,2}}{2\Delta r}+\frac{1}{\left [ 3\left ( \Delta r\right ) \right ] ^{2}}\frac{T_{4,1}-2T_{4,2}+T_{4,3}}{\Delta \theta ^{2}} & =-200\nonumber \\ T_{3,2}\left ( \frac{1}{\Delta r^{2}}-\frac{1}{6\Delta r^{2}}\right ) +T_{4,2}\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{9\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,1}\left ( \frac{1}{9\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,3}\left ( \frac{1}{9\Delta r^{2}\Delta \theta ^{2}}\right ) & =-200\nonumber \\ T_{3,2}\left ( \frac{5}{6\Delta r^{2}}\right ) +T_{4,2}\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{9\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,1}\left ( \frac{1}{9\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,3}\left ( \frac{1}{9\Delta r^{2}\Delta \theta ^{2}}\right ) & =-200 \tag{4,2} \end{align}
This completes first internal grid line on the right half. Now we move another \(\Delta \theta \) anti-clock wise and process the central line.
At node \(\left ( 2,3\right ) \)
\begin{align} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =-200\nonumber \\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =-200\nonumber \\ \frac{T_{1,3}-2T_{2,3}+T_{3,3}}{\Delta r^{2}}+\frac{1}{\Delta r}\frac{T_{3,3}-T_{1,3}}{2\Delta r}+\frac{1}{\Delta r^{2}}\frac{T_{2,2}-2T_{2,3}+T_{2,4}}{\Delta \theta ^{2}} & =-200\nonumber \\ T_{1,1}\left ( \frac{1}{2\Delta r^{2}}\right ) +T_{2,3}\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{3,3}\left ( \frac{3}{2\Delta r^{2}}\right ) +T_{2,2}\left ( \frac{1}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{2,4}\left ( \frac{1}{\Delta r^{2}\Delta \theta ^{2}}\right ) & =-200 \tag{2,3} \end{align}
At node \(\left ( 3,3\right ) \)
\begin{align} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =-200\nonumber \\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =-200\nonumber \\ \frac{T_{2,3}-2T_{3,3}+T_{4,3}}{\Delta r^{2}}+\frac{1}{2\Delta r}\frac{T_{4,3}-T_{2,3}}{2\Delta r}+\frac{1}{4\Delta r^{2}}\frac{T_{3,2}-2T_{3,3}+T_{3,4}}{\Delta \theta ^{2}} & =-200\nonumber \\ T_{2,3}\left ( \frac{3}{4\Delta r^{2}}\right ) +T_{3,3}\left ( \frac{-2}{\Delta r^{2}}-\frac{1}{2\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,3}\left ( \frac{5}{4\Delta r^{2}}\right ) +T_{3,2}\left ( \frac{1}{4\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{3,4}\left ( \frac{1}{4\Delta r^{2}\Delta \theta ^{2}}\right ) & =-200 \tag{3,3} \end{align}
At node \(\left ( 4,3\right ) \)
\begin{align} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =-200\nonumber \\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =-200\nonumber \\ \frac{T_{3,3}-2T_{4,3}+T_{5,3}}{\Delta r^{2}}+\frac{1}{3\Delta r}\frac{T_{5,3}-T_{3,3}}{2\Delta r}+\frac{1}{9\Delta r^{2}}\frac{T_{4,2}-2T_{4,3}+T_{4,4}}{\Delta \theta ^{2}} & =-200\nonumber \end{align}
But \(T_{5,3}=0\) since at boundary, hence
\begin{align} \frac{T_{3,3}-2T_{4,3}}{\Delta r^{2}}+\frac{1}{3\Delta r}\frac{-T_{3,3}}{2\Delta r}+\frac{1}{9\Delta r^{2}}\frac{T_{4,2}-2T_{4,3}+T_{4,4}}{\Delta \theta ^{2}} & =-200\nonumber \\ T_{3,3}\left ( \frac{5}{6\Delta r^{2}}\right ) +T_{4,3}\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{9\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,2}\left ( \frac{1}{9\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,4}\left ( \frac{1}{9\Delta r^{2}\Delta \theta ^{2}}\right ) & =-200 \tag{4,3} \end{align}
Now we move to the central line. On this line the PDE is \(\frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}}=-100\).
Hence at node \(\left ( 2,4\right ) \) we have
\begin{align*} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =-100\\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =-100\\ \frac{T_{1,4}-2T_{2,4}+T_{3,4}}{\Delta r^{2}}+\frac{1}{\Delta r}\frac{T_{3,4}-T_{1,4}}{2\Delta r}+\frac{1}{\Delta r^{2}}\frac{T_{2,3}-2T_{2,4}+T_{2,5}}{\Delta \theta ^{2}} & =-100\\ T_{1,4}\left ( \frac{1}{\Delta r^{2}}-\frac{1}{2\Delta r^{2}}\right ) +T_{2,4}\left ( -\frac{2}{\Delta r^{2}}-\frac{2}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{3,4}\left ( \frac{1}{\Delta r^{2}}+\frac{1}{2\Delta r^{2}}\right ) +T_{2,3}\left ( \frac{1}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{2,5}\left ( \frac{1}{\Delta r^{2}\Delta \theta ^{2}}\right ) & =-100 \end{align*}
But \(T_{1,4}=T_{1,1}\). This is the same node. Hence the above becomes
\begin{equation} T_{1,1}\left ( \frac{1}{2\Delta r^{2}}\right ) +T_{2,4}\left ( -\frac{2}{\Delta r^{2}}-\frac{2}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{3,4}\left ( \frac{3}{2\Delta r^{2}}\right ) +T_{2,3}\left ( \frac{1}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{2,5}\left ( \frac{1}{\Delta r^{2}\Delta \theta ^{2}}\right ) =-100 \tag{2,4} \end{equation}
At node \(\left ( 3,4\right ) \)
\begin{align} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =-100\nonumber \\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =-100\nonumber \\ \frac{T_{2,4}-2T_{3,4}+T_{4,4}}{\Delta r^{2}}+\frac{1}{2\Delta r}\frac{T_{4,4}-T_{2,4}}{2\Delta r}+\frac{1}{4\Delta r^{2}}\frac{T_{3,3}-2T_{3,4}+T_{3,5}}{\Delta \theta ^{2}} & =-100\nonumber \\ T_{2,4}\left ( \frac{3}{4\Delta r^{2}}\right ) +T_{3,4}\left ( \frac{-2}{\Delta r^{2}}-\frac{1}{2\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,4}\left ( \frac{5}{4\Delta r^{2}}\right ) +T_{3,3}\left ( \frac{1}{4\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{3,5}\left ( \frac{1}{4\Delta r^{2}\Delta \theta ^{2}}\right ) & =-100 \tag{3,4} \end{align}
At node \(\left ( 4,4\right ) \)
\begin{align} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =-100\nonumber \\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =-100\nonumber \\ \frac{T_{3,4}-2T_{4,4}+T_{5,4}}{\Delta r^{2}}+\frac{1}{3\Delta r}\frac{T_{5,4}-T_{3,4}}{2\Delta r}+\frac{1}{9\Delta r^{2}}\frac{T_{4,3}-2T_{4,4}+T_{4,5}}{\Delta \theta ^{2}} & =-100\nonumber \end{align}
But \(T_{5,4}=0\) since at B.C. hence
\begin{align} \frac{T_{3,4}-2T_{4,4}}{\Delta r^{2}}+\frac{1}{3\Delta r}\frac{-T_{3,4}}{2\Delta r}+\frac{1}{9\Delta r^{2}}\frac{T_{4,3}-2T_{4,4}+T_{4,5}}{\Delta \theta ^{2}} & =-100\nonumber \\ T_{3,4}\left ( \frac{5}{6\Delta r^{2}}\right ) +T_{4.4}\left ( \frac{-2}{\Delta r^{2}}+\frac{-2}{9\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,3}\left ( \frac{1}{9\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,5}\left ( \frac{1}{9\Delta r^{2}\Delta \theta ^{2}}\right ) & =-100 \tag{4,4} \end{align}
This completes the central line, now we move \(\Delta \theta \) anti-clock wise and process the next grid line.
Node \(\left ( 2,5\right ) \) is in the left side, where the PDE is \(\frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}}=0\). Hence
\begin{align} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =0\nonumber \\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =0\nonumber \\ \frac{T_{1,5}-2T_{2,5}+T_{3,5}}{\Delta r^{2}}+\frac{1}{\Delta r}\frac{T_{3,5}-T_{1,5}}{2\Delta r}+\frac{1}{\Delta r^{2}}\frac{T_{2,4}-2T_{2,5}+T_{2,6}}{\Delta \theta ^{2}} & =0\nonumber \\ T_{1,1}\left ( \frac{1}{2\Delta r^{2}}\right ) +T_{2,5}\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{3,5}\left ( \frac{3}{2\Delta r^{2}}\right ) +T_{2,4}\left ( \frac{1}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{2,6}\left ( \frac{1}{\Delta r^{2}\Delta \theta ^{2}}\right ) & =0 \tag{2,5} \end{align}
At node \(\left ( 3,5\right ) \)
\begin{align} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =0\nonumber \\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =0\nonumber \\ \frac{T_{2,5}-2T_{3,5}+T_{4,5}}{\Delta r^{2}}+\frac{1}{2\Delta r}\frac{T_{4,5}-T_{2,5}}{2\Delta r}+\frac{1}{4\Delta r^{2}}\frac{T_{3,4}-2T_{3,5}+T_{3,6}}{\Delta \theta ^{2}} & =0\nonumber \\ T_{2,5}\left ( \frac{3}{4\Delta r^{2}}\right ) +T_{3,5}\left ( \frac{-2}{\Delta r^{2}}-\frac{1}{2\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,5}\left ( \frac{5}{4\Delta r^{2}}\right ) +T_{3,4}\left ( \frac{1}{4\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{3,6}\left ( \frac{1}{4\Delta r^{2}\Delta \theta ^{2}}\right ) & =0 \tag{3,5} \end{align}
At node \(\left ( 4,5\right ) \)
\begin{align} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =0\nonumber \\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =0\nonumber \\ \frac{T_{3,5}-2T_{4,5}+T_{5,5}}{\Delta r^{2}}+\frac{1}{3\Delta r}\frac{T_{5,5}-T_{3,5}}{2\Delta r}+\frac{1}{9\Delta r^{2}}\frac{T_{4,4}-2T_{4,5}+T_{4,6}}{\Delta \theta ^{2}} & =0\nonumber \end{align}
But \(T_{5,5}=0\) since at boundary
\begin{align} \frac{T_{3,5}-2T_{4,5}}{\Delta r^{2}}+\frac{1}{3\Delta r}\frac{-T_{3,5}}{2\Delta r}+\frac{1}{9\Delta r^{2}}\frac{T_{4,4}-2T_{4,5}+T_{4,6}}{\Delta \theta ^{2}} & =0\nonumber \\ T_{3,5}\left ( \frac{5}{6\Delta r^{2}}\right ) +T_{4,5}\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{9\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,4}\left ( \frac{1}{9\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,6}\left ( \frac{1}{9\Delta r^{2}\Delta \theta ^{2}}\right ) & =0 \tag{4,5} \end{align}
At node \(\left ( 2,6\right ) \)
\begin{align} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =0\nonumber \\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =0\nonumber \\ \frac{T_{1,6}-2T_{2,6}+T_{3,6}}{\Delta r^{2}}+\frac{1}{\Delta r}\frac{T_{3,6}-T_{1,6}}{2\Delta r}+\frac{1}{\Delta r^{2}}\frac{T_{2,5}-2T_{2,6}+T_{2,7}}{\Delta \theta ^{2}} & =0\nonumber \\ T_{1,1}\left ( \frac{1}{2\Delta r^{2}}\right ) +T_{2,6}\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{3,6}\left ( \frac{3}{2\Delta r^{2}}\right ) +T_{2,5}\left ( \frac{1}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{2,7}\left ( \frac{1}{\Delta r^{2}\Delta \theta ^{2}}\right ) & =0 \tag{2,6} \end{align}
At node \(\left ( 3,6\right ) \)
\begin{align} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =0\nonumber \\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =0\nonumber \\ \frac{T_{2,6}-2T_{3,6}+T_{4,6}}{\Delta r^{2}}+\frac{1}{2\Delta r}\frac{T_{4,6}-T_{2,6}}{2\Delta r}+\frac{1}{4\Delta r^{2}}\frac{T_{3,5}-2T_{3,6}+T_{3,7}}{\Delta \theta ^{2}} & =0\nonumber \\ T_{2,6}\left ( \frac{3}{4\Delta r^{2}}\right ) +T_{3,6}\left ( \frac{-2}{\Delta r^{2}}-\frac{1}{2\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,6}\left ( \frac{5}{4\Delta r^{2}}\right ) +T_{3,5}\left ( \frac{1}{4\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{3,7}\left ( \frac{1}{4\Delta r^{2}\Delta \theta ^{2}}\right ) & =0 \tag{3,6} \end{align}
At node \(\left ( 4,6\right ) \)
\begin{align*} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =0\\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =0\\ \frac{T_{3,6}-2T_{4,6}+T_{5,6}}{\Delta r^{2}}+\frac{1}{3\Delta r}\frac{T_{5,6}-T_{3,6}}{2\Delta r}+\frac{1}{9\Delta r^{2}}\frac{T_{4,5}-2T_{4,6}+T_{4,7}}{\Delta \theta ^{2}} & =0 \end{align*}
But \(T_{5,6}=0\) since at boundary hence
\begin{align} \frac{T_{3,6}-2T_{4,6}}{\Delta r^{2}}+\frac{1}{3\Delta r}\frac{-T_{3,6}}{2\Delta r}+\frac{1}{9\Delta r^{2}}\frac{T_{4,5}-2T_{4,6}+T_{4,7}}{\Delta \theta ^{2}} & =0\nonumber \\ T_{3,6}\left ( \frac{5}{6\Delta r^{2}}\right ) +T_{4,6}\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{9\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,5}\left ( \frac{1}{9\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,7}\left ( \frac{1}{9\Delta r^{2}\Delta \theta ^{2}}\right ) & =0 \tag{4,6} \end{align}
We now move to the bottom grid line at \(\theta =\pi \), where it is insulated.
At node \(\left ( 2,7\right ) \)
\begin{align*} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =0\\ \frac{T_{1,7}-2T_{2,7}+T_{3,7}}{\Delta r^{2}}+\frac{1}{\Delta r}\frac{T_{3,7}-T_{1,7}}{2\Delta r}+\frac{1}{\Delta r^{2}}\frac{T_{2,6}-2T_{2,7}+T_{2,8}}{\Delta \theta ^{2}} & =0 \end{align*}
But \(T_{2,8}=T_{2,5}\) due to insulation and \(T_{1,7}=T_{1,1}\) since same node, hence above becomes
\begin{align} \frac{T_{1,1}-2T_{2,7}+T_{3,7}}{\Delta r^{2}}+\frac{1}{\Delta r}\frac{T_{3,7}-T_{1,1}}{2\Delta r}+\frac{1}{\Delta r^{2}}\frac{2T_{2,6}-2T_{2,7}}{\Delta \theta ^{2}} & =0\nonumber \\ T_{1,1}\left ( \frac{1}{2\Delta r^{2}}\right ) +T_{2,7}\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{3,7}\left ( \frac{3}{2\Delta r^{2}}\right ) +T_{2,6}\left ( \frac{2}{\Delta r^{2}\Delta \theta ^{2}}\right ) & =0 \tag{2,7} \end{align}
At node \(\left ( 3,7\right ) \)
\begin{align*} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =0\\ \frac{T_{i-1,j}-2T_{ij}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =0\\ \frac{T_{2,7}-2T_{3,7}+T_{4,7}}{\Delta r^{2}}+\frac{1}{2\Delta r}\frac{T_{4,7}-T_{2,7}}{2\Delta r}+\frac{1}{4\Delta r^{2}}\frac{T_{3,6}-2T_{3,7}+T_{3,8}}{\Delta \theta ^{2}} & =0 \end{align*}
But \(T_{3,8}=T_{3,6}\) due to insulation, hence
\begin{align} \frac{T_{2,7}-2T_{3,7}+T_{4,7}}{\Delta r^{2}}+\frac{1}{2\Delta r}\frac{T_{4,7}-T_{2,7}}{2\Delta r}+\frac{1}{4\Delta r^{2}}\frac{2T_{3,6}-2T_{3,7}}{\Delta \theta ^{2}} & =0\nonumber \\ T_{2,7}\left ( \frac{3}{4\Delta r^{2}}\right ) +T_{3,7}\left ( \frac{-2}{\Delta r^{2}}-\frac{1}{2\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,7}\left ( \frac{5}{4\Delta r^{2}}\right ) +T_{3,6}\left ( \frac{1}{2\Delta r^{2}\Delta \theta ^{2}}\right ) & =0 \tag{3,7} \end{align}
At node \(\left ( 4,7\right ) \)
\begin{align*} \frac{\partial ^{2}T}{\partial r^{2}}+\frac{1}{r}\frac{\partial T}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}T}{\partial \theta ^{2}} & =0\\ \frac{T_{i-1,j}-2T_{i,j}+T_{i+1,j}}{\Delta r^{2}}+\frac{1}{\left ( i-1\right ) \left ( \Delta r\right ) }\frac{T_{i+1,j}-T_{i-1,j}}{2\Delta r}+\frac{1}{\left [ \left ( i-1\right ) \left ( \Delta r\right ) \right ] ^{2}}\frac{T_{i,j-1}-2T_{ij}+T_{i,j+1}}{\Delta \theta ^{2}} & =0\\ \frac{T_{3,7}-2T_{4,7}+T_{5,7}}{\Delta r^{2}}+\frac{1}{3\Delta r}\frac{T_{5,7}-T_{3,7}}{2\Delta r}+\frac{1}{9\Delta r^{2}}\frac{T_{4,6}-2T_{4,7}+T_{4,8}}{\Delta \theta ^{2}} & =0 \end{align*}
But \(T_{4,8}=T_{4,6}\) due to insulation and \(T_{5,7}=0\) since on boundary, hence
\begin{align} \frac{T_{3,7}-2T_{4,7}}{\Delta r^{2}}+\frac{1}{3\Delta r}\frac{-T_{3,7}}{2\Delta r}+\frac{1}{9\Delta r^{2}}\frac{2T_{4,6}-2T_{4,7}}{\Delta \theta ^{2}} & =0\nonumber \\ T_{3,7}\left ( \frac{5}{6\Delta r^{2}}\right ) +T_{4,7}\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{9\Delta r^{2}\Delta \theta ^{2}}\right ) +T_{4,6}\left ( \frac{2}{9\Delta r^{2}\Delta \theta ^{2}}\right ) & =0 \tag{4,7} \end{align}
Now we are able to see the \(A\) matrix structure. The number of unknowns is \(22\). Let \(\alpha _{1}=\left ( \frac{-2}{\Delta r^{2}}-\frac{1}{2\Delta r^{2}\Delta \theta ^{2}}\right ) ,\alpha _{2}=\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{\Delta r^{2}\Delta \theta ^{2}}\right ) ,\alpha _{3}=\left ( \frac{-2}{\Delta r^{2}}-\frac{2}{9\Delta r^{2}\Delta \theta ^{2}}\right ) ,\beta =\frac{1}{\Delta r^{2}},\gamma =\frac{1}{\Delta r^{2}\Delta \theta ^{2}}\) then the above equations can now be written as \(Ax=f\)
\[\begin{pmatrix} 1 & -\frac{1}{12} & 0 & 0 & -\frac{1}{6} & 0 & 0 & -\frac{1}{6} & 0 & 0 & -\frac{1}{6} & 0 & 0 & -\frac{1}{6} & 0 & 0 & -\frac{1}{6} & 0 & 0 & -\frac{1}{12} & 0 & 0\\ \frac{1}{2}\beta & \alpha _{2} & \frac{3}{2}\beta & 0 & 2\gamma & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & \frac{3}{4}\beta & \alpha _{1} & \frac{5}{4}\beta & 0 & \frac{1}{2}\gamma & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & \frac{5}{6}\beta & \alpha _{3} & 0 & 0 & \frac{2}{9}\gamma & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ \frac{1}{2}\beta & \gamma & 0 & 0 & \alpha _{2} & \frac{3}{2}\beta & 0 & \gamma & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & \frac{1}{4}\gamma & 0 & \frac{3}{4}\beta & \alpha _{1} & \frac{5}{4}\beta & 0 & \frac{1}{4}\gamma & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & \frac{1}{9}\gamma & 0 & \frac{5}{4}\beta & \alpha _{3} & 0 & 0 & \frac{1}{9}\gamma & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ \frac{1}{2}\beta & 0 & 0 & 0 & \gamma & 0 & 0 & \alpha _{2} & \frac{3}{2}\beta & 0 & \gamma & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & \frac{1}{4}\gamma & 0 & \frac{3}{4}\beta & \alpha _{1} & \frac{5}{4}\beta & 0 & \frac{1}{4}\gamma & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{9}\gamma & 0 & \frac{5}{6}\beta & \alpha _{3} & 0 & 0 & \frac{1}{9}\gamma & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ \frac{1}{2}\beta & 0 & 0 & 0 & 0 & 0 & 0 & \gamma & 0 & 0 & \alpha _{2} & \frac{3}{2}\beta & 0 & \gamma & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{4}\gamma & 0 & \frac{3}{4}\beta & \alpha _{1} & \frac{5}{4}\beta & 0 & \frac{1}{4}\gamma & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{9}\gamma & 0 & \frac{5}{6}\beta & \alpha _{3} & 0 & 0 & \frac{1}{9}\gamma & 0 & 0 & 0 & 0 & 0 & 0\\ \frac{1}{2}\beta & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \gamma & 0 & 0 & \alpha _{3} & \frac{3}{2}\beta & 0 & \gamma & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{4}\gamma & 0 & \frac{3}{4}\beta & \alpha _{1} & \frac{5}{4}\beta & 0 & \frac{1}{4}\gamma & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{9}\gamma & 0 & \frac{5}{6}\beta & \alpha _{3} & 0 & 0 & \frac{1}{9}\gamma & 0 & 0 & 0\\ \frac{1}{2}\beta & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \gamma & 0 & \alpha _{3} & \frac{3}{2}\beta & 0 & \gamma & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{4}\gamma & 0 & \frac{3}{4}\beta & \alpha _{1} & \frac{5}{4}\beta & 0 & \frac{1}{4}\gamma & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{9}\gamma & 0 & \frac{5}{6}\beta & \alpha _{3} & 0 & 0 & \frac{1}{9}\gamma \\ \frac{1}{2}\beta & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 2\gamma & 0 & 0 & \alpha _{2} & \frac{3}{2}\beta & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{2}\gamma & 0 & \frac{3}{4}\beta & \alpha _{1} & \frac{5}{4}\beta \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{2}{9}\gamma & 0 & \frac{5}{6}\beta & \alpha _{3}\end{pmatrix}\begin{pmatrix} T_{11}\\ T_{21}\\ T_{31}\\ T_{41}\\ T_{22}\\ T_{32}\\ T_{42}\\ T_{23}\\ T_{33}\\ T_{43}\\ T_{24}\\ T_{34}\\ T_{44}\\ T_{25}\\ T_{35}\\ T_{45}\\ T_{26}\\ T_{36}\\ T_{46}\\ T_{27}\\ T_{37}\\ T_{47}\end{pmatrix} =\begin{pmatrix} 25\Delta r^{2}\\ -200\\ -200\\ -200\\ -200\\ -200\\ -200\\ -200\\ -200\\ -200\\ -100\\ -100\\ -100\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0\\ 0 \end{pmatrix} \]
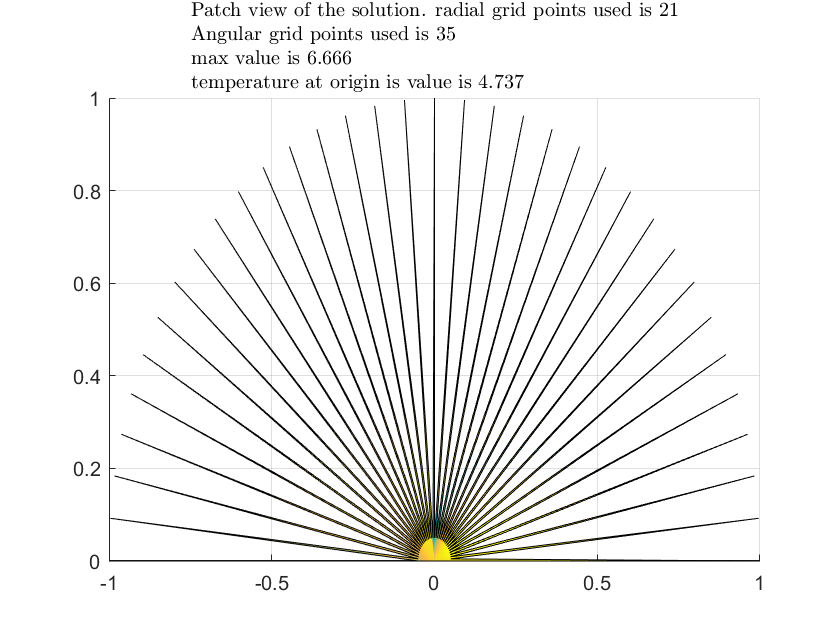
We now can see the pattern to use. The above is solved using \(Ax=f\) in Matlab.
The solution below. The temperature at origin was found to be \(4.737\) degrees and the maximum was \(6.666\) degrees.