Obtain two distinct Laurent expansions for \(f\left ( z\right ) =\frac{3z+1}{z^{2}-1}\) around \(z=1\) and tell where each converges.
Solution
\(f\left ( z\right ) \) has singularities at \(z=\pm 1\) and the expansion is around one of these singularities. Looking at the diagram
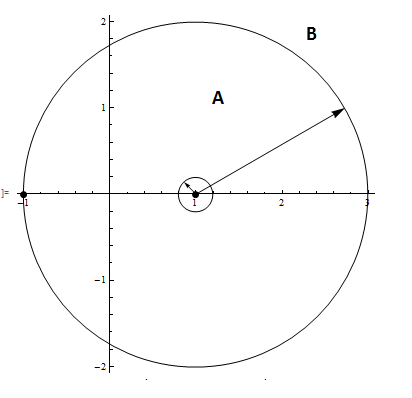
Region \(A\) is annulus between \(z=1\) and \(z=-1\) but does not include \(z=1\) where the small circle is shown since that is a singularity. Region \(B\) is all the region outside the large circle shown.\[ f\left ( z\right ) =\frac{3z+1}{\left ( z-1\right ) \left ( z+1\right ) }=\frac{2}{z-1}+\frac{1}{z+1}\] Region A
For \(\frac{2}{z-1}\), since its pole is at \(z=1\) and so we expand outwards, and hence it is already in form of Laurent series around \(z=1\), and for \(\frac{1}{z+1}\) since its pole is at \(z=-1\), hence we expand inwards, and so it is expanded in Taylor series\[ f\left ( z\right ) =\overset{Laurent}{\overbrace{\frac{2}{z-1}}}+\overset{Taylor}{\overbrace{\frac{1}{z+1}}}\] Looking at the second term above, expand in Taylor series\begin{align*} \frac{1}{z+1} & =\frac{1}{\left ( z-1\right ) +1+1}=\frac{1}{\left ( z-1\right ) +2}=\frac{1}{2}\frac{1}{1+\frac{1}{2}\left ( z-1\right ) }\\ & =\frac{1}{2}\sum \limits _{n=0}^{\infty }\left ( -1\right ) ^{n}\left ( \frac{1}{2}\right ) ^{n}\left ( z-1\right ) ^{n}\qquad \left \vert z-1\right \vert <2 \end{align*}
Therefore, for region A\begin{align*} f\left ( z\right ) & =\frac{2}{z-1}+\frac{1}{2}\sum \limits _{n=0}^{\infty }\left ( -1\right ) ^{n}\left ( \frac{1}{2}\right ) ^{n}\left ( z-1\right ) ^{n}\\ & =\frac{2}{z-1}+\frac{1}{2}\left ( 1-\frac{1}{2}\left ( z-1\right ) +\frac{1}{4}\left ( z-1\right ) ^{2}-\frac{1}{16}\left ( z-1\right ) ^{3}+\cdots \right ) \\ & =\frac{2}{z-1}+\frac{1}{2}-\frac{1}{4}\left ( z-1\right ) +\frac{1}{8}\left ( z-1\right ) ^{2}-\frac{1}{16}\left ( z-1\right ) ^{3}+\cdots \end{align*}
This is valid for \(0<\left \vert z-1\right \vert <2,z\neq 1\)
Region B
This is the region outside the large circle to infinity. Since expanding outwards, both terms will use Laurent series now.\[ f\left ( z\right ) =\overset{Laurent}{\overbrace{\frac{2}{z-1}}}+\overset{Laurent}{\overbrace{\frac{1}{z+1}}}\] \(\frac{2}{z-1}\) is already in Laurent series, for the second term\begin{align*} \frac{1}{z+1} & =\frac{1}{\left ( z-1\right ) +1+1}=\frac{1}{\left ( z-1\right ) +2}=\frac{1}{\left ( z-1\right ) }\frac{1}{1+\frac{2}{z-1}}\\ & =\frac{1}{\left ( z-1\right ) }\sum \limits _{n=0}^{\infty }\left ( -1\right ) ^{n}\frac{2^{n}}{\left ( z-1\right ) ^{n}}\qquad \left \vert z-1\right \vert >2 \end{align*}
Hence\begin{align*} f\left ( z\right ) & =\frac{2}{z-1}+\frac{1}{\left ( z-1\right ) }\sum \limits _{n=0}^{\infty }\left ( -1\right ) ^{n}\frac{2^{n}}{\left ( z-1\right ) ^{n}}\\ & =\frac{2}{z-1}+\frac{1}{\left ( z-1\right ) }\left ( 1-\frac{2}{\left ( z-1\right ) }+\frac{4}{\left ( z-1\right ) ^{2}}-\frac{8}{\left ( z-1\right ) ^{3}}+\cdots \right ) \\ & =\frac{2}{z-1}+\frac{1}{z-1}-\frac{2}{\left ( z-1\right ) ^{2}}+\frac{4}{\left ( z-1\right ) ^{3}}-\frac{8}{\left ( z-1\right ) ^{4}}+\cdots \\ & =\frac{3}{z-1}-\frac{2}{\left ( z-1\right ) ^{2}}+\frac{4}{\left ( z-1\right ) ^{3}}-\frac{8}{\left ( z-1\right ) ^{4}}+\cdots \end{align*}
This is valid for \(\left \vert z-1\right \vert >2\)
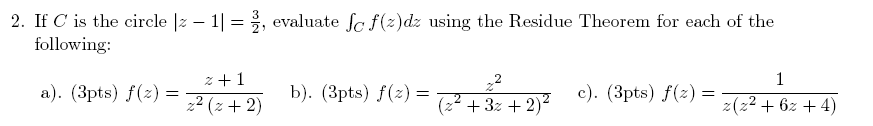
\(f\left ( z\right ) =\frac{z+1}{z^{2}\left ( z+2\right ) }\), Poles are \(z=0\) order 2 and \(z=-2\) order 1. The pole \(z=-2\) is outside \(C\) hence it will not have an effect. To find the residue due to pole \(z=0\)\begin{align*} residue\left ( z=0\right ) & =\frac{1}{\left ( 2-1\right ) !}\lim _{z\rightarrow 0}\frac{d}{dz}\left ( z^{2}f\left ( z\right ) \right ) \\ & =\lim _{z\rightarrow 0}\frac{d}{dz}\left ( z^{2}\frac{z+1}{z^{2}\left ( z+2\right ) }\right ) \\ & =\lim _{z\rightarrow 0}\frac{d}{dz}\left ( \frac{z+1}{z+2}\right ) \\ & =\lim _{z\rightarrow 0}\left ( \frac{1}{z+2}-\frac{\left ( z+1\right ) }{\left ( z+2\right ) ^{2}}\right ) \\ & =\frac{1}{2}-\frac{1}{4}\\ & =\frac{1}{4} \end{align*}
Hence \begin{align*} \oint f\left ( z\right ) dz & =2\pi i\left ( \frac{1}{4}\right ) \\ & =\frac{1}{2}\pi i \end{align*}
\(f\left ( z\right ) =\frac{z^{2}}{\left ( z^{2}+3z+2\right ) ^{2}}\) the poles are the roots of \(\left ( z^{2}+3z+2\right ) ^{2}=0\) which is \(\left ( \left ( z+2\right ) \left ( z+1\right ) \right ) ^{2}=0\) or \(\left ( z+2\right ) ^{2}\left ( z+1\right ) ^{2}=0\), hence poles at \(\left ( z+2\right ) ^{2}=0\) or \(z=-2\) and \(\left ( z+1\right ) ^{2}=0\) or \(z=-1\) Only pole at \(z=-1\) is inside \(C\). This is order \(2\) since the denominator is order 2. Hence\begin{align*} residue\left ( z=-1\right ) & =\frac{1}{\left ( 2-1\right ) !}\lim _{z\rightarrow -1}\frac{d}{dz}\left ( \left ( z+1\right ) ^{2}f\left ( z\right ) \right ) \\ & =\lim _{z\rightarrow -1}\frac{d}{dz}\left ( \left ( z+1\right ) ^{2}\frac{z^{2}}{\left ( z+2\right ) ^{2}\left ( z+1\right ) ^{2}}\right ) \\ & =\lim _{z\rightarrow -1}\frac{d}{dz}\left ( \frac{z^{2}}{\left ( z+1\right ) ^{2}}\right ) \\ & =\lim _{z\rightarrow -1}\left ( \frac{2z}{\left ( z+2\right ) ^{2}}-2z^{2}\left ( z+2\right ) ^{-3}\right ) \\ & =\lim _{z\rightarrow -1}\left ( \frac{2z}{\left ( z+2\right ) ^{2}}-\frac{2z^{2}}{\left ( z+2\right ) ^{3}}\right ) \\ & =\left ( \frac{-2}{\left ( -1+2\right ) ^{2}}-\frac{2\left ( -1\right ) ^{2}}{\left ( -1+2\right ) ^{3}}\right ) \\ & =\left ( -2-2\right ) \\ & =-4 \end{align*}
Hence\begin{align*} \oint f\left ( z\right ) dz & =2\pi i\left ( -4\right ) \\ & =-8\pi i \end{align*}
\(f\left ( z\right ) =\frac{1}{z\left ( z^{2}+6z+4\right ) }=\frac{1}{z\left ( z-\left ( \sqrt{5}-3\right ) \right ) \left ( z-\left ( -\sqrt{5}-3\right ) \right ) }=\frac{1}{z\left ( z-\left ( \sqrt{5}-3\right ) \right ) \left ( z-\left ( -\sqrt{5}-3\right ) \right ) }\). Since \(\sqrt{5}-3=-5.\,\allowbreak 236\,1\) and \(-\sqrt{5}-3=-0.763\,93\) then only \(z=\left ( -\sqrt{5}-3\right ) \) is inside \(C\).
Hence poles are \(z=0\) and \(z=\left ( -\sqrt{5}-3\right ) \) and both is order 1.\begin{align*} residue\left ( z=0\right ) & =\lim _{z\rightarrow 0}\left ( zf\left ( z\right ) \right ) \\ & =\lim _{z\rightarrow 0}\left ( z\frac{1}{z\left ( z^{2}+6z+4\right ) }\right ) \\ & =\lim _{z\rightarrow 0}\left ( \frac{1}{\left ( z^{2}+6z+4\right ) }\right ) \\ & =\frac{1}{4} \end{align*}
And\begin{align*} residue\left ( z=\left ( -\sqrt{5}-3\right ) \right ) & =\lim _{z\rightarrow \left ( -\sqrt{5}-3\right ) }\left ( \left ( z-\left ( -\sqrt{5}-3\right ) \right ) f\left ( z\right ) \right ) \\ & =\lim _{z\rightarrow \left ( -\sqrt{5}-3\right ) }\left ( \left ( z-\left ( -\sqrt{5}-3\right ) \right ) \frac{1}{z\left ( z-\left ( \sqrt{5}-3\right ) \right ) \left ( z-\left ( -\sqrt{5}-3\right ) \right ) }\right ) \\ & =\lim _{z\rightarrow \left ( -\sqrt{5}-3\right ) }\left ( \frac{1}{z\left ( z-\left ( \sqrt{5}-3\right ) \right ) }\right ) \\ & =\frac{1}{\left ( -\sqrt{5}-3\right ) \left ( \left ( -\sqrt{5}-3\right ) -\left ( \sqrt{5}-3\right ) \right ) }\\ & =\frac{1}{\left ( -\sqrt{5}-3\right ) \left ( -\sqrt{5}-3-\sqrt{5}+3\right ) }\\ & =\frac{1}{\left ( -\sqrt{5}-3\right ) \left ( -2\sqrt{5}\right ) }\\ & =\frac{1}{10+6\sqrt{5}} \end{align*}
Hence\begin{align*} \oint f\left ( z\right ) dz & =2\pi i\left ( \frac{1}{4}+\frac{1}{10+6\sqrt{5}}\right ) \\ & =\left ( \frac{1}{2}+\frac{1}{5+3\sqrt{5}}\right ) \pi i\\ & =0.5854\pi i \end{align*}
Show that \(f\left ( z\right ) =\frac{\cosh \left ( z\right ) -1}{\sinh \left ( z\right ) -z}\) has simple pole at \(z=0\) and find its residue there.
Solution
Expanding \(\cosh \left ( z\right ) \) and \(\sinh \left ( z\right ) \) in series gives \[ f\left ( z\right ) =\frac{\left ( 1+\frac{z^{2}}{2!}+\frac{z^{4}}{4!}+\frac{z^{6}}{6!}\right ) -1}{\left ( z+\frac{z^{3}}{3!}+\frac{z^{5}}{5!}+\frac{z^{7}}{7!}\right ) -z}=\frac{\frac{z^{2}}{2!}+\frac{z^{4}}{4!}+\frac{z^{6}}{6!}}{\frac{z^{3}}{3!}+\frac{z^{5}}{5!}+\frac{z^{7}}{7!}}\] Divide by \(z^{2}\)\begin{align*} f\left ( z\right ) & =\frac{\frac{1}{2!}+\frac{z^{2}}{4!}+\frac{z^{4}}{6!}}{\frac{z}{3!}+\frac{z^{3}}{5!}+\frac{z^{5}}{7!}}\\ & =\frac{\frac{1}{2!}+\frac{z^{2}}{4!}+\frac{z^{4}}{6!}}{z\left ( \frac{1}{3!}+\frac{z^{2}}{5!}+\frac{z^{4}}{7!}\right ) } \end{align*}
Therefore, \(f\left ( z\right ) \) has simple pole at \(z=0\). The residue is\begin{align*} residue\left ( z=0\right ) & =\lim _{z\rightarrow 0}\left ( zf\left ( z\right ) \right ) \\ & =\lim _{z\rightarrow 0}\left ( z\frac{\cosh \left ( z\right ) -1}{\sinh \left ( z\right ) -z}\right ) \\ & =\lim _{z\rightarrow 0}\left ( z\frac{\frac{1}{2!}+\frac{z^{2}}{4!}+\frac{z^{4}}{6!}}{z\left ( \frac{1}{3!}+\frac{z^{2}}{5!}+\frac{z^{4}}{7!}\right ) }\right ) \\ & =\lim _{z\rightarrow 0}\left ( \frac{\frac{1}{2!}+\frac{z^{2}}{4!}+\frac{z^{4}}{6!}}{\left ( \frac{1}{3!}+\frac{z^{2}}{5!}+\frac{z^{4}}{7!}\right ) }\right ) \\ & =\frac{\frac{1}{2!}}{\frac{1}{3!}}\\ & =\frac{6}{2}\\ & =3 \end{align*}
Evaluate the following using the method of residues (a) \(\int _{0}^{\pi }\frac{\cos \left ( 2\theta \right ) }{5+4\cos \theta }d\theta \) (b)\(\int _{0}^{2\pi }\frac{\sin ^{2}\theta }{a+b\cos \theta }d\theta \) where \(0<b<a\) and (c) \(\int _{-\infty }^{\infty }\frac{x^{2}}{1+x^{6}}dx\)
Let \[ I=\int _{0}^{\pi }\frac{\cos \left ( 2\theta \right ) }{5+4\cos \theta }d\theta \] Since the integrand is even then\[ I=\frac{1}{2}\int _{-\pi }^{\pi }\frac{\cos \left ( 2\theta \right ) }{5+4\cos \theta }d\theta \] Let \(I_{1}=\int _{-\pi }^{\pi }\frac{\cos \left ( 2\theta \right ) }{5+4\cos \theta }d\theta \), hence\[ I=\frac{1}{2}I_{1}\] Now we evaluate \(I_{1}\). Let \(z=re^{i\theta }\), and for a unit circle, \(r=1\), hence \(dz=ie^{i\theta }d\theta \) or \(d\theta =-i\frac{dz}{e^{i\theta }}=-i\frac{dz}{z}\). Now we need to convert the integrand from function of \(\theta \) to function of \(z.\)
\(\cos \left ( 2\theta \right ) =\frac{e^{i2\theta }+e^{-i2\theta }}{2}=\frac{1}{2}\left ( z^{2}+z^{-2}\right ) \) and \(\cos \theta =\frac{e^{i\theta }+e^{-i\theta }}{2}=\frac{1}{2}\left ( z+z^{-1}\right ) \), therefore the integral becomes\[ I_{1}=\operatorname{Re}\oint \frac{\frac{1}{2}\left ( z^{2}+z^{-2}\right ) }{5+4\left ( \frac{1}{2}\left ( z+z^{-1}\right ) \right ) }\left ( -i\frac{dz}{z}\right ) \] The contour is over the unit circle. Let \(I_{2}=\oint \frac{\frac{1}{2}\left ( z^{2}+z^{-2}\right ) }{5+4\left ( \frac{1}{2}\left ( z+z^{-1}\right ) \right ) }\left ( -i\frac{dz}{z}\right ) \,\), hence \(I_{1}=\operatorname{Re}\left ( I_{2}\right ) \) and now we evaluate \(I_{2}.\) \begin{align*} I_{2} & =\oint \frac{\frac{1}{2}\left ( z^{2}+z^{-2}\right ) }{5+4\left ( \frac{1}{2}\left ( z+z^{-1}\right ) \right ) }\left ( -i\frac{dz}{z}\right ) \\ & =-\frac{i}{2}\oint \frac{z^{2}+z^{-2}}{5+2\left ( z+z^{-1}\right ) }\frac{dz}{z}\\ & =-\frac{i}{2}\oint \frac{\frac{z^{4}+1}{z^{2}}}{5+2\left ( \frac{z^{2}+1}{z}\right ) }\frac{dz}{z}\\ & =-\frac{i}{2}\oint \frac{\frac{z^{4}+1}{z^{2}}}{\frac{5z+2\left ( z^{2}+1\right ) }{z}}\frac{dz}{z}\\ & =-\frac{i}{2}\oint \frac{z^{4}+1}{5z^{2}+2z\left ( z^{2}+1\right ) }\frac{dz}{z}\\ & =-\frac{i}{2}\oint \frac{z^{4}+1}{5z^{3}+2z^{2}\left ( z^{2}+1\right ) }dz\\ & =-\frac{i}{2}\oint \frac{z^{4}+1}{5z^{3}+2z^{4}+2z^{2}}dz\\ & =-\frac{i}{2}\oint \frac{z^{4}+1}{z^{2}\left ( 2z^{2}+5z+2\right ) }dz\\ & =-\frac{i}{4}\oint \frac{z^{4}+1}{z^{2}\left ( z^{2}+\frac{5}{2}z+1\right ) }dz\\ & =-\frac{i}{4}\oint \frac{z^{4}+1}{z^{2}\left ( z+2\right ) \left ( z+\frac{1}{2}\right ) }dz \end{align*}
The poles are \(z=0\) of order \(2\) and \(z=-2\) and \(z=-\frac{1}{2}\), hence only \(z=-\frac{1}{2}\) is inside the unit circle. Lets find the residues of each now. \begin{align*} \text{residue}\left ( z=0\right ) & =\lim _{z\rightarrow 0}\frac{1}{\left ( 2-1\right ) !}\frac{d}{dz}\left ( z^{2}f\left ( z\right ) \right ) =\frac{d}{dz}\left ( \frac{z^{4}+1}{\left ( z+2\right ) \left ( z+\frac{1}{2}\right ) }\right ) \\ & =\lim _{z\rightarrow 0}\left ( \frac{2}{\left ( 2z^{2}+5z+2\right ) ^{2}}\left ( 4z^{5}+15z^{4}+8z^{3}-4z-5\right ) \right ) \\ & =\left ( \frac{2}{\left ( 2\right ) ^{2}}\left ( -5\right ) \right ) =-\frac{5}{2} \end{align*}
And\begin{align*} \text{residue}\left ( z=-\frac{1}{2}\right ) & =\lim _{z\rightarrow -\frac{1}{2}}\left ( \left ( z+\frac{1}{2}\right ) f\left ( z\right ) \right ) =\lim _{z\rightarrow -\frac{1}{2}}\left ( \frac{z^{4}+1}{z^{2}\left ( z+2\right ) }\right ) \\ & =\frac{\left ( -\frac{1}{2}\right ) ^{4}+1}{\left ( -\frac{1}{2}\right ) ^{2}\left ( -\frac{1}{2}+2\right ) }\\ & =\frac{17}{6} \end{align*}
Hence \begin{align*} \oint \frac{z^{4}+1}{z^{2}\left ( z+2\right ) \left ( z+\frac{1}{2}\right ) }dz & =2\pi i\left ( -\frac{5}{2}+\frac{17}{6}\right ) \\ & =\frac{2}{3}i\pi \end{align*}
Hence\begin{align*} -\frac{i}{4}\oint \frac{z^{4}+1}{z^{2}\left ( z+2\right ) \left ( z+\frac{1}{2}\right ) }dz & =\left ( -\frac{i}{4}\right ) \frac{2}{3}i\pi \\ & =\left ( \frac{1}{4}\right ) \frac{2}{3}\pi \\ & =\frac{1}{6}\pi \end{align*}
Hence\[ I_{2}=\frac{1}{6}\pi \] But \(I_{1}=\operatorname{Re}\left ( I_{2}\right ) \), hence \(I_{1}=\frac{1}{3}\pi \). And \(I=\frac{1}{2}I_{1}\), hence \[ I=\frac{1}{12}\pi \]
\(I=\int _{0}^{2\pi }\frac{\sin ^{2}\theta }{a+b\cos \theta }d\theta \) where \(0<b<a\).
We need to convert this to contour integral over the unit circle. Let \(z=re^{i\theta }\), and for a unit circle, \(r=1\), hence \(dz=ie^{i\theta }d\theta \) or \(d\theta =-i\frac{dz}{e^{i\theta }}=-i\frac{dz}{z}\). Now we need to convert the integrand from function of \(\theta \) to function of \(z.\)
\(\cos \left ( \theta \right ) =\frac{e^{i\theta }+e^{-i\theta }}{2}=\frac{1}{2}\left ( z+z^{-1}\right ) \) and \(\sin \theta =\frac{e^{i\theta }-e^{-i\theta }}{2i}=\frac{1}{2i}\left ( z-z^{-1}\right ) \), Hence \begin{align*} \sin ^{2}\theta & =\left ( \frac{1}{2i}\left ( z-z^{-1}\right ) \right ) ^{2}\\ & =\frac{-1}{4}\left ( z-z^{-1}\right ) ^{2}=\frac{-1}{4}\left ( z^{2}+z^{-2}-2\right ) \end{align*}
Therefore the integral becomes\begin{align*} I & =\oint \frac{\frac{-1}{4}\left ( z^{2}+z^{-2}-2\right ) }{a+b\frac{1}{2}\left ( z+z^{-1}\right ) }\left ( -i\frac{dz}{z}\right ) \\ & =\frac{i}{4}\oint \frac{z^{2}+z^{-2}-2}{a+b\frac{1}{2}\left ( \frac{z^{2}+1}{z}\right ) }\frac{dz}{z}\\ & =\frac{i}{4}\oint \frac{\frac{z^{4}+1-2z^{2}}{z^{2}}}{az+b\frac{1}{2}\left ( z^{2}+1\right ) }dz\\ & =\frac{i}{2}\oint \frac{1}{z^{2}}\frac{z^{4}-2z^{2}+1}{2az+b\left ( z^{2}+1\right ) }dz\\ & =\frac{i}{2}\oint \frac{1}{z^{2}}\frac{z^{4}-2z^{2}+1}{bz^{2}+2az+b}dz\\ & =\frac{i}{2b}\oint \frac{1}{z^{2}}\frac{z^{4}-2z^{2}+1}{z^{2}+\frac{2a}{b}z+1}dz \end{align*}
Roots of \(z^{2}+\frac{2a}{b}z+1\) are \(\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}=\frac{-\frac{2a}{b}\pm \sqrt{\left ( \frac{2a}{b}\right ) ^{2}-4}}{2}=-\frac{a}{b}\pm \frac{1}{2}\sqrt{\frac{4a^{2}}{b^{2}}-4}=-\frac{a}{b}\pm \sqrt{\left ( \frac{a}{b}\right ) ^{2}-1}\) Hence \[ r_{1}=-\frac{a}{b}-\sqrt{\left ( \frac{a}{b}\right ) ^{2}-1}\] and \[ r_{2}=-\frac{a}{b}+\sqrt{\left ( \frac{a}{b}\right ) ^{2}-1}\] Since \(a>b\) then \(r_{1}\) is outside the unit circle. but \(r_{2}\) is inside. The integral is now\[ I=\frac{i}{2b}\oint \frac{1}{z^{2}}\frac{z^{4}-2z^{2}+1}{\left ( z-r_{1}\right ) \left ( z-r_{2}\right ) }dz \] pole at \(z=0\) or order 2. To find the residue for this pole\begin{align*} res\left ( z=0\right ) & =\lim _{z\rightarrow 0}\frac{1}{\left ( 2-1\right ) !}\left ( z^{2}f\left ( z\right ) \right ) \\ & =\lim _{z\rightarrow 0}\left ( \frac{z^{4}-2z^{2}+1}{\left ( z-r_{1}\right ) \left ( z-r_{2}\right ) }\right ) \\ & =\frac{1}{\left ( -r_{1}\right ) \left ( -r_{2}\right ) }\\ & =\frac{1}{r_{1}r_{2}} \end{align*}
To find the residue for this \(r_{2}\)\begin{align*} res\left ( z=r_{2}\right ) & =\lim _{z\rightarrow r_{2}}\left ( \left ( z-r_{2}\right ) f\left ( z\right ) \right ) \\ & =\lim _{z\rightarrow r_{2}}\left ( \frac{z^{4}-2z^{2}+1}{z^{2}\left ( z-r_{1}\right ) }\right ) \\ & =\frac{r_{2}^{4}-2r_{2}^{2}+1}{r_{2}^{2}\left ( r_{2}-r_{1}\right ) } \end{align*}
Therefore, \begin{align*} I & =\frac{i}{2b}\oint \frac{1}{z^{2}}\frac{z^{4}-2z^{2}+1}{z^{2}+\frac{2a}{b}z+1}dz\\ & =\frac{i}{2b}\left ( 2\pi i\left ( \frac{1}{r_{1}r_{2}}+\frac{r_{2}^{4}-2r_{2}^{2}+1}{r_{2}^{2}\left ( r_{2}-r_{1}\right ) }\right ) \right ) \\ & =\frac{-\pi }{b}\left ( \frac{1}{r_{1}r_{2}}+\frac{r_{2}^{4}-2r_{2}^{2}+1}{r_{2}^{2}\left ( r_{2}-r_{1}\right ) }\right ) \end{align*}
This is the value of the integral, where \(r_{1},r_{2}\) are given as above. To simplify this final result, CAS was used for this step\begin{align*} I & =\frac{-\pi }{b}\left ( \frac{1}{\left ( -\frac{a}{b}-\sqrt{\frac{a^{2}}{b^{2}}-1}\right ) \left ( -\frac{a}{b}+\sqrt{\frac{a^{2}}{b^{2}}-1}\right ) }+\frac{\left ( -\frac{a}{b}+\sqrt{\frac{a^{2}}{b^{2}}-1}\right ) ^{4}-2\left ( -\frac{a}{b}+\sqrt{\frac{a^{2}}{b^{2}}-1}\right ) ^{2}+1}{\left ( -\frac{a}{b}+\sqrt{\frac{a^{2}}{b^{2}}-1}\right ) \left ( \left ( -\frac{a}{b}+\sqrt{\frac{a^{2}}{b^{2}}-1}\right ) -\left ( -\frac{a}{b}-\sqrt{\frac{a^{2}}{b^{2}}-1}\right ) \right ) }\right ) \\ & =-\frac{\pi }{b}\left ( 1+\frac{2\sqrt{\left ( a-b\right ) \left ( a+b\right ) }}{b}\right ) \\ & =-\frac{\pi }{b}\left ( 1+\frac{2\sqrt{a^{2}-b^{2}}}{b}\right ) \end{align*}
Therefore\[ I=\left ( \frac{-b-2\sqrt{a^{2}-b^{2}}}{b^{2}}\right ) \pi \]
\[ I=\int _{-\infty }^{\infty }\frac{x^{2}}{1+x^{6}}dx \]
We first need to determine if the integral over the upper half plan vanish when \(R\rightarrow \infty \), and for this we just need to show that \(\lim _{z\rightarrow \infty }zf\left ( z\right ) =0\) where \(f\left ( z\right ) =\frac{z^{2}}{1+z^{6}}\) Hence\begin{align*} \lim _{z\rightarrow \infty }zf\left ( z\right ) & =\lim _{z\rightarrow \infty }\left ( z\frac{z^{2}}{1+z^{6}}\right ) \\ & =\lim _{z\rightarrow \infty }\left ( \frac{z^{3}}{1+z^{6}}\right ) =\lim _{z\rightarrow \infty }\left ( \frac{1}{\frac{1}{z^{3}}+z^{3}}\right ) =\frac{1}{0+\infty }=0 \end{align*}
Hence the integral becomes\[ I=\int _{-\infty }^{\infty }\frac{z^{2}}{1+z^{6}}dz=2\pi i\sum \limits ^{UHP}res\left ( f\left ( z\right ) \right ) \] Now need to find the poles in UHP. From \(f\left ( z\right ) =\frac{z^{2}}{1+z^{6}}\) the poles are the roots of \(1+z^{6}=0\) or \(z^{6}=-1\), therefore \(z=-1^{\left ( \frac{1}{6}\right ) }\), but \(-1=e^{i\pi }\) Hence need to spread \(6\) poles around \(2\pi \), which means the phase changes by \(\frac{2\pi }{6}\) between each, hence \begin{align*} z & =\left \{ e^{i\frac{\pi }{6}},e^{i\frac{\pi }{6}+\frac{2\pi }{6}},e^{i\frac{\pi }{6}+\frac{4\pi }{6}},e^{i\frac{\pi }{6}+\frac{6\pi }{6}},e^{i\frac{\pi }{6}+\frac{8\pi }{6}},e^{i\frac{\pi }{6}+\frac{10\pi }{6}}\right \} \\ & =\left \{ e^{i\frac{\pi }{6}},e^{i\frac{3\pi }{6}},e^{i\frac{5\pi }{6}},e^{i\frac{7\pi }{6}},e^{i\frac{9\pi }{6}},e^{i\frac{11\pi }{6}}\right \} \end{align*}
Now need to find which of these roots is in UHP. Looking at the phase, we see that \(e^{i\frac{\pi }{6}},e^{i\frac{3\pi }{6}},e^{i\frac{5\pi }{6}}\) are in UHP since phase is less than \(\pi \). So now we need to find residue at each pole. \[ I=2\pi i\left ( res\left ( e^{i\frac{\pi }{6}}\right ) +res\left ( e^{i\frac{\pi }{2}}\right ) +res\left ( e^{i\frac{5\pi }{6}}\right ) \right ) \] Using \(\left [ \frac{N\left ( z\right ) }{D^{\prime }\left ( z\right ) }\right ] _{z->z_{o}}\) to find residue at \(z=z_{0}\) (since each is a simple pole). But \(D^{\prime }\left ( z\right ) =\frac{d}{dz}\left ( 1+z^{6}\right ) =6z^{5}\), hence\begin{align*} res\left ( e^{i\frac{\pi }{6}}\right ) & =\left ( \frac{z^{2}}{6z^{5}}\right ) _{z=e^{i\frac{\pi }{6}}}\\ & =\frac{e^{i\frac{2\pi }{6}}}{6e^{i\frac{5\pi }{6}}}=\frac{e^{i\left ( \frac{2\pi }{6}-\frac{5\pi }{6}\right ) }}{6}=\frac{1}{6}e^{i\frac{-\pi }{2}}=\frac{-i}{6} \end{align*}
And\begin{align*} res\left ( e^{i\frac{3\pi }{6}}\right ) & =\left ( \frac{z^{2}}{6z^{5}}\right ) _{z=e^{i\frac{3\pi }{6}}}\\ & =\frac{e^{i\frac{6\pi }{6}}}{6e^{i\frac{15\pi }{6}}}=\frac{e^{i\left ( \frac{6\pi }{6}-\frac{15\pi }{6}\right ) }}{6}=\frac{1}{6}e^{i\frac{-9\pi }{6}}=\frac{1}{6}e^{-i\frac{3}{2}\pi }=\frac{i}{6} \end{align*}
And\begin{align*} res\left ( e^{i\frac{5\pi }{6}}\right ) & =\left ( \frac{z^{2}}{6z^{5}}\right ) _{z=e^{i\frac{5\pi }{6}}}\\ & =\frac{e^{i\frac{10\pi }{6}}}{6e^{i\frac{25\pi }{6}}}=\frac{e^{i\left ( \frac{10\pi }{6}-\frac{25\pi }{6}\right ) }}{6}=\frac{1}{6}e^{i\frac{-15\pi }{6}}=\frac{1}{6}e^{-i\frac{\pi }{2}}=\frac{-i}{6} \end{align*}
Therefore\begin{align*} I & =2\pi i\left ( res\left ( e^{i\frac{\pi }{6}}\right ) +res\left ( e^{i\frac{\pi }{2}}\right ) +res\left ( e^{i\frac{5\pi }{6}}\right ) \right ) \\ & =2\pi i\left ( \frac{-i}{6}+\frac{i}{6}-\frac{i}{6}\right ) \end{align*}
Hence\[ I=\frac{\pi }{3}\]
Evaluate the following integration by integrating around a suitably indented contour in the complex plane \(I=\int _{0}^{\infty }\frac{\sin \left ( ax\right ) }{x\left ( x^{2}+b^{2}\right ) }dx\) where \(a>0\), \(b>0\)
Solution\begin{align*} I & =\frac{1}{2}\int _{-\infty }^{\infty }\frac{\sin \left ( ax\right ) }{x\left ( x^{2}+b^{2}\right ) }dx\\ & =\frac{1}{2}\operatorname{Im}\left ( \int _{-\infty }^{\infty }\frac{e^{iaz}}{z\left ( z^{2}+b^{2}\right ) }dz\right ) \\ & =\frac{1}{2}\operatorname{Im}\left ( \int _{-\infty }^{\infty }\frac{e^{iaz}}{z\left ( z-ib\right ) \left ( z+ib\right ) }dz\right ) \end{align*}
To show that the UHP integral vanish we need to show that \(\lim _{\left \vert z\right \vert \rightarrow \infty }zf\left ( z\right ) =0\) then we can just do the integration over the real line using residues of poles in UHP. \[ \lim _{\left \vert z\rightarrow \infty \right \vert }\left ( z\frac{e^{iaz}}{z\left ( z^{2}+b^{2}\right ) }\right ) =\lim _{\left \vert z\rightarrow \infty \right \vert }\left ( \frac{e^{iaz}}{z^{2}+b^{2}}\right ) \rightarrow 0 \] Since \(\left \vert e^{iaz}\right \vert =1.\) The poles at the real line are \(z=0\) and poles in complex plane are \(z=-ib\) and \(z=ib\). Since \(b>0\) then \(z=ib\) is only in UHP. \[ I=\frac{1}{2}\operatorname{Im}\left ( \pi i\left [ res\left ( 0\right ) \right ] +2\pi i\left [ res\left ( ib\right ) \right ] \right ) \] To find residue at \(z=0\), using \[ res\left ( 0\right ) =\lim _{z\rightarrow 0}\left ( z\frac{e^{iaz}}{z\left ( z^{2}+b^{2}\right ) }\right ) =\lim _{z\rightarrow 0}\left ( \frac{e^{iaz}}{\left ( z^{2}+b^{2}\right ) }\right ) =\frac{1}{b^{2}}\] And\[ res\left ( ib\right ) =\lim _{z\rightarrow ib}\left ( \left ( z-ib\right ) \frac{e^{iaz}}{z\left ( z-ib\right ) \left ( z+ib\right ) }\right ) =\lim _{z\rightarrow ib}\left ( \frac{e^{iaz}}{z\left ( z+ib\right ) }\right ) =\frac{e^{-ab}}{-2b^{2}}\] Therefore\begin{align*} I & =\frac{1}{2}\operatorname{Im}\left ( \pi i\left [ \frac{1}{b^{2}}\right ] +2\pi i\left [ \frac{e^{-ab}}{-2b^{2}}\right ] \right ) \\ & =\frac{1}{2}\left ( \pi \left [ \frac{1}{b^{2}}\right ] +2\pi \left [ \frac{e^{-ab}}{-2b^{2}}\right ] \right ) \\ & =\frac{1}{2}\left ( \frac{\pi }{b^{2}}-\frac{\pi e^{-ab}}{b^{2}}\right ) \end{align*}
Hence\[ I=\frac{\pi -\pi e^{-ab}}{2b^{2}}\]
Evaluate the integrals (a) \(\int _{-\infty }^{\infty }\frac{e^{px}-e^{qx}}{1-e^{x}}dx\) where \(0<p<1,0<q<1\) (b) \(\int _{0}^{\infty }\frac{\ln \left ( x^{2}+1\right ) }{1+x^{2}}dx\)
Solution
\[ I=\int _{-\infty }^{\infty }\frac{e^{px}-e^{qx}}{1-e^{x}}dx \] Break the integral into 2 and use the rectangle grid method to show that each leg of the integral vanish\[ I=I_{1}-I_{2}\] Where\begin{align*} I_{1} & =\int _{-\infty }^{\infty }\frac{e^{pz}}{1-e^{z}}dz\\ I_{2} & =\int _{-\infty }^{\infty }\frac{e^{qz}}{1-e^{z}}dz \end{align*}
Looking at \(I_{1}\) for now.\[ \int _{-\infty }^{\infty }\frac{e^{pz}}{1-e^{z}}dz=\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz+\overset{leg1}{\overbrace{\int _{R}^{R+2\pi i}\frac{e^{pz}}{1-e^{z}}dz}}+\int _{R+2\pi i}^{-R+2\pi i}\frac{e^{pz}}{1-e^{z}}dz+\overset{leg2}{\overbrace{\int _{-R+2\pi i}^{-R}\frac{e^{pz}}{1-e^{z}}dz}}\] looking at leg1 integral, \(\int _{R}^{R+2\pi i}\frac{e^{pz}}{1-e^{z}}dz\). Let \(z=2\pi it+R\) or \(t=\frac{z-R}{2\pi i}\), hence \(dt=\frac{dz}{2\pi i}\). When \(z=R,t=0\) and when \(z=R+2\pi i,t=1\), hence the integral for leg1 becomes\[ \int _{0}^{1}\frac{e^{p\left ( 2\pi it+R\right ) }}{1-e^{2\pi it+R}}2\pi idt=2\pi i\int _{0}^{1}\frac{e^{p\left ( 2\pi it+R\right ) }}{1-e^{2\pi it+R}}dt \] Now we need to show that the above goes to zero as \(R\) goes to infinity. Writing the above as\[ 2\pi i\int _{0}^{1}\frac{e^{p2\pi it}e^{pR}}{1-e^{2\pi it}e^{R}}dt=2\pi i\int _{0}^{1}\frac{e^{p2\pi it}}{e^{-pR}-e^{2\pi it}e^{R\left ( 1-p\right ) }}dt \] Now \(\lim _{R\rightarrow \infty }e^{-pR}=0\) since \(p>0\) and \(\lim _{R\rightarrow \infty }e^{R\left ( 1-p\right ) }=\infty \) since \(1-p\) is positive, since \(p<1\). Therefore the above becomes\[ 2\pi i\int _{0}^{1}\frac{e^{p2\pi it}}{0-e^{2\pi it}\infty }dt \] And since \(\left \vert e^{ix}\right \vert =1\) then the integrand becomes \(\frac{1}{-\infty }\rightarrow 0\), hence the integral vanishes. We need to do the same for the second leg\[ \int _{-R+2\pi i}^{-R}\frac{e^{pz}}{1-e^{z}}dz \] Let \(z=2\pi it+R\) or \(t=\frac{z+R}{2\pi i}\), hence \(dt=\frac{dz}{2\pi i}\). When \(z=-R,t=0\) and when \(z=-R+2\pi i,t=1\), hence the integral for leg2 becomes\[ \int _{1}^{0}\frac{e^{p\left ( 2\pi it+R\right ) }}{1-e^{2\pi it+R}}2\pi idt=2\pi i\int _{1}^{0}\frac{e^{p\left ( 2\pi it+R\right ) }}{1-e^{2\pi it+R}}dt \] Now we need to show that the above goes to zero as \(R\) goes to infinity. Writing the above as\[ 2\pi i\int _{0}^{1}\frac{e^{p2\pi it}e^{qR}}{1-e^{2\pi it}e^{R}}dt=2\pi i\int _{0}^{1}\frac{e^{p2\pi it}}{e^{-qR}-e^{2\pi it}e^{R\left ( 1-p\right ) }}dt \] Now \(\lim _{R\rightarrow \infty }e^{-pR}=0\) since \(p>0\) and \(\lim _{R\rightarrow \infty }e^{R\left ( 1-p\right ) }=\infty \) since \(1-p\) is positive, since \(p<1\). Therefore the above becomes\[ 2\pi i\int _{0}^{1}\frac{e^{p2\pi it}}{0-e^{2\pi it}\infty }dt \] And since \(\left \vert e^{ix}\right \vert =1\) then the integrand becomes \(\frac{1}{-\infty }\rightarrow 0\), hence the integral vanishes. So we are left with these now\[ \int _{-\infty }^{\infty }\frac{e^{pz}}{1-e^{z}}dz=\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz+\int _{R+2\pi i}^{-R+2\pi i}\frac{e^{pz}}{1-e^{z}}dz \] Now we use \(t=z-2\pi i\) for the top edge only. \(dt=dz,\) when \(z=R+2\pi i,t=R\) and when \(z=-R+2\pi i,t=-R\), hence the above becomes\begin{align*} \int _{-\infty }^{\infty }\frac{e^{pz}}{1-e^{z}}dz & =\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz+\int _{R}^{-R}\frac{e^{p\left ( t+2\pi i\right ) }}{1-e^{t}}dt\\ & =\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz-\int _{-R}^{R}\frac{e^{p\left ( t+2\pi i\right ) }}{1-e^{t}}dt\\ & =\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz-\int _{-R}^{R}\frac{e^{pt}e^{p2\pi i}}{1-e^{t}}dt\\ & =\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz-e^{p2\pi i}\int _{-R}^{R}\frac{e^{pt}}{1-e^{t}}dt\\ & =\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz-e^{p2\pi i}\int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz\\ & =\left ( 1-e^{p2\pi i}\right ) \int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz \end{align*}
But in the limit \(\lim _{R\rightarrow \infty }\) \(\left ( 1-e^{p2\pi i}\right ) \int _{-R}^{R}\frac{e^{pz}}{1-e^{z}}dz\rightarrow \left ( 1-e^{p2\pi i}\right ) \int _{-\infty }^{\infty }\frac{e^{pz}}{1-e^{z}}dz=2\pi i\sum res\) Hence\[ \int _{-\infty }^{\infty }\frac{e^{pz}}{1-e^{z}}dz=\frac{1}{\left ( 1-e^{p2\pi i}\right ) }\left ( 2\pi i\sum ^{UHP}res+\pi i\sum ^{line}res\right ) \] Now we need to find poles in the rectangle. Poles of \(f\left ( z\right ) =\frac{e^{pz}}{1-e^{z}}\) are \(e^{z}=1\), hence \(z=0,i2\pi ,i4\pi ,\cdots \) so only \(z=0\) and \(z=i2\pi \) is of interest to use. The pole at \(z=0\) is on the real line, so this get \(i\pi \) and the pole at \(i2\pi \) get \(i2\pi \) contribution. But \[ res\left ( 2\pi i\right ) =\left [ \frac{N\left ( z\right ) }{D^{\prime }\left ( z\right ) }\right ] _{z=2\pi i}=\left [ \frac{e^{pz}}{-e^{z}}\right ] _{z=2\pi i}=\frac{e^{p2\pi i}}{-e^{2\pi i}}=-e^{p2\pi i}\] And\[ res\left ( 0\right ) =\left [ \frac{N\left ( z\right ) }{D^{\prime }\left ( z\right ) }\right ] _{z=0}=\left [ \frac{e^{pz}}{-e^{z}}\right ] _{z=0}=-1 \] Hence\begin{align*} \int _{-\infty }^{\infty }\frac{e^{pz}}{1-e^{z}}dz & =\frac{1}{\left ( 1-e^{p2\pi i}\right ) }\left ( 2\pi i\left ( -e^{p2\pi i}\right ) +\pi i\left ( -1\right ) \right ) \\ & =\frac{-2\pi ie^{2\pi ip}-\pi i}{\left ( 1-e^{p2\pi i}\right ) }\\ & =\pi i\left ( \frac{-2e^{2\pi ip}-1}{1-e^{p2\pi i}}\right ) \end{align*}
For \(I_{2}\), the result will be similar, hence\[ I_{2}=\pi i\left ( \frac{-2e^{2\pi iq}-1}{1-e^{q2\pi i}}\right ) \] Hence\begin{align*} I & =I_{1}-I_{2}\\ & =\pi i\left ( \frac{-2e^{2\pi ip}-1}{1-e^{p2\pi i}}\right ) -\pi i\left ( \frac{-2e^{2\pi iq}-1}{1-e^{q2\pi i}}\right ) \\ & =\pi i\left ( \frac{-2e^{2\pi ip}-1}{1-e^{p2\pi i}}-\frac{-2e^{2\pi iq}-1}{1-e^{q2\pi i}}\right ) \end{align*}
\[ I=\int _{0}^{\infty }\frac{\ln \left ( x^{2}+1\right ) }{1+x^{2}}dx \] parameterize it as \[ I\left ( a\right ) =\int _{0}^{\infty }\frac{\ln \left ( ax^{2}+1\right ) }{1+x^{2}}dx \] Differentia w.r.t. \(a\)\begin{align*} I^{\prime }\left ( a\right ) & =\int _{0}^{\infty }\frac{d}{da}\frac{\ln \left ( ax^{2}+1\right ) }{1+x^{2}}dx\\ & =\int _{0}^{\infty }\frac{x^{2}}{\left ( 1+x^{2}\right ) \left ( 1+ax^{2}\right ) }dx\\ & =\frac{1}{2}\int _{-\infty }^{\infty }\frac{z^{2}}{\left ( 1+z^{2}\right ) \left ( 1+az^{2}\right ) }dz\\ & =\frac{1}{2a}\int _{-\infty }^{\infty }\frac{z^{2}}{\left ( 1+z^{2}\right ) \left ( \frac{1}{a}+z^{2}\right ) }dz\\ & =\frac{1}{2a}\int _{-\infty }^{\infty }\frac{z^{2}}{\left ( z-i\right ) \left ( z+i\right ) \left ( z-\frac{i}{\sqrt{a}}\right ) \left ( z+\frac{i}{\sqrt{a}}\right ) }dz \end{align*}
Poles are at \(z=\pm i\) and \(z=\pm \frac{i}{\sqrt{a}}\). Pole \(z=\{i,\frac{i}{\sqrt{a}}\}\) are in UHP assuming \(a>0\). Residue for \(z=i\) is\begin{align*} res\left ( i\right ) & =\lim _{z\rightarrow i}\frac{z^{2}}{\left ( z+i\right ) \left ( z-\frac{i}{\sqrt{a}}\right ) \left ( z+\frac{i}{\sqrt{a}}\right ) }\\ & =\frac{-1}{\left ( 2i\right ) \left ( i-\frac{i}{\sqrt{a}}\right ) \left ( i+\frac{i}{\sqrt{a}}\right ) }\\ & =-i\frac{a}{2a-2} \end{align*}
Residue for \(z=\frac{i}{\sqrt{a}}\)\begin{align*} res\left ( i\sqrt{a}\right ) & =\lim _{z\rightarrow \frac{i}{\sqrt{a}}}\frac{z^{2}}{\left ( z-i\right ) \left ( z+i\right ) \left ( z+\frac{i}{\sqrt{a}}\right ) }\\ & =\frac{\frac{-1}{a}}{\left ( \frac{i}{\sqrt{a}}-i\right ) \left ( \frac{i}{\sqrt{a}}+i\right ) \left ( \frac{i}{\sqrt{a}}+\frac{i}{\sqrt{a}}\right ) }\\ & =i\frac{\sqrt{a}}{2a-2} \end{align*}
Hence\begin{align*} \frac{1}{2a}\int _{-\infty }^{\infty }\frac{z^{2}}{\left ( z-i\right ) \left ( z+i\right ) \left ( z-\frac{i}{\sqrt{a}}\right ) \left ( z+\frac{i}{\sqrt{a}}\right ) }dz & =\frac{1}{2a}2\pi i\left ( -i\frac{a}{2a-2}+i\frac{\sqrt{a}}{2a-2}\right ) \\ & =\frac{1}{2}\frac{\pi }{a+\sqrt{a}} \end{align*}
Therefore\[ I^{\prime }\left ( a\right ) =\frac{1}{2}\frac{\pi }{a+\sqrt{a}}\] Integrate\begin{align*} I\left ( a\right ) & =\frac{\pi }{2}\int \frac{1}{a+\sqrt{a}}da\\ & =\frac{\pi }{2}2\log \left ( \sqrt{a}+1\right ) +C\\ & =\pi \log \left ( \sqrt{a}+1\right ) +C \end{align*}
To find \(C,\) from \[ I\left ( a\right ) =\int _{0}^{\infty }\frac{\ln \left ( ax^{2}+1\right ) }{1+x^{2}}dx \] we see that at \(a=0\) then \(I\left ( 0\right ) =0\,\ \)hence\begin{align*} 0 & =\pi \log \left ( 0+1\right ) +C\\ C & =0 \end{align*}
Hence\[ I\left ( a\right ) =\pi \log \left ( \sqrt{a}+1\right ) \] To obtain the integral we started with, let \(a=1\), hence\begin{align*} I\left ( 1\right ) & =\int _{0}^{\infty }\frac{\ln \left ( x^{2}+1\right ) }{1+x^{2}}dx\\ & =\left [ \pi \log \left ( \sqrt{a}+1\right ) \right ] _{a=1}\\ & =\pi \log \left ( 1+1\right ) \end{align*}
Hence \[ \int _{0}^{\infty }\frac{\ln \left ( x^{2}+1\right ) }{1+x^{2}}dx=\pi \log \left ( 2\right ) \]
Determine the Laplace inversion for (a) \(F\left ( s\right ) =\frac{s+1}{s^{2}\left ( s^{2}+s+1\right ) }\) (b)\(F\left ( s\right ) =\frac{1}{\left ( a+b\right ) \cosh \left ( a\sqrt{s}\right ) }\)
Using Bromwich formula\begin{align*} f\left ( t\right ) & =\frac{1}{2\pi i}\lim _{b\rightarrow \infty }\int _{a-ib}^{a+ib}F\left ( s\right ) e^{st}ds\\ & =\frac{1}{2\pi i}\lim _{b\rightarrow \infty }\int _{a-ib}^{a+ib}\frac{s+1}{s^{2}\left ( s^{2}+s+1\right ) }e^{st}ds \end{align*}
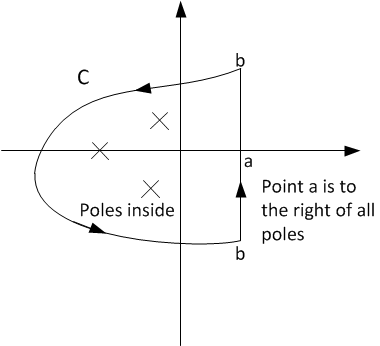
The integral is broken into 2 parts, the vertical leg and the integration of the curve shown above labeled \(C\). \[ f\left ( t\right ) =\frac{1}{2\pi i}\lim _{b\rightarrow \infty }\left ( \int _{a-ib}^{a+ib}\frac{s+1}{s^{2}\left ( s^{2}+s+1\right ) }e^{st}ds+\oint \limits _{C}\frac{s+1}{s^{2}\left ( s^{2}+s+1\right ) }e^{st}ds\right ) \] We can use the residue theorem on the above integral, but provided the function \(F\left ( s\right ) e^{st}\) is analytic inside the curve shown above (except of course at the poles, if any, inside the curve). Proof that \(F\left ( s\right ) e^{st}\) satisfies this condition is hence assumed. The proof was not given in class. So we need to calculate the residues of \(F\left ( s\right ) e^{st}\) for all the poles.\[ f\left ( t\right ) =\frac{1}{2\pi i}\left ( 2\pi i\sum \limits _{i=1}^{poles}res\left ( F\left ( s_{i}e^{s_{i}t}\right ) \right ) \right ) \] So let us find the poles and the residue of each. Given \(\frac{s+1}{s^{2}\left ( s^{2}+s+1\right ) }e^{st}=\frac{s+1}{s^{2}\left ( s-\left ( -\frac{1}{2}i\sqrt{3}-\frac{1}{2}\right ) \right ) \left ( s-\left ( \frac{1}{2}i\sqrt{3}-\frac{1}{2}\right ) \right ) }e^{st}\) hence the poles are \(s=0\) or order \(2\) and \(s_{1}=\left ( -\frac{1}{2}i\sqrt{3}-\frac{1}{2}\right ) \) and \(s_{2}=\left ( \frac{1}{2}i\sqrt{3}-\frac{1}{2}\right ) \).
Residue for \(s=0\) is \begin{align*} res\left ( 0\right ) & =\lim _{s\rightarrow 0}\frac{d}{ds}\left ( \frac{s^{2}\left ( s+1\right ) }{s^{2}\left ( s-s_{1}\right ) \left ( s-s_{2}\right ) }e^{st}\right ) \\ & =\lim _{s\rightarrow 0}\frac{d}{ds}\left ( \frac{\left ( s+1\right ) }{\left ( s-s_{1}\right ) \left ( s-s_{2}\right ) }e^{(st)}\right ) \\ & =t \end{align*}
And\begin{align*} res\left ( s_{1}\right ) & =\lim _{s\rightarrow s_{1}}\frac{\left ( s+1\right ) }{s^{2}\left ( s-s_{2}\right ) }e^{st}\\ & =-\frac{ie^{-\frac{1}{2}\left ( 1+i\sqrt{3}\right ) t}}{\sqrt{3}} \end{align*}
And\begin{align*} res\left ( s_{2}\right ) & =\lim _{s\rightarrow s_{2}}\frac{\left ( s+1\right ) }{s^{2}\left ( s-s_{1}\right ) }e^{st}\\ & =-\frac{(-i+\sqrt{3})e^{\frac{1}{2}\left ( 1+i\sqrt{3}\right ) t}}{3i+\sqrt{3}} \end{align*}
Therefore,\begin{align*} f\left ( t\right ) & =t-\frac{ie^{-\frac{1}{2}\left ( 1+i\sqrt{3}\right ) t}}{\sqrt{3}}-\frac{(-i+\sqrt{3})e^{\frac{1}{2}\left ( 1+i\sqrt{3}\right ) t}}{3i+\sqrt{3}}\\ & =t-\frac{2e^{-\frac{t}{2}}\sin \left ( \frac{\sqrt{3}t}{2}\right ) }{\sqrt{3}} \end{align*}
The setup is similar to part(a) and not will be repeated, we will go the step of finding the residues. For this, we need to first find the poles of \[ F\left ( s\right ) e^{st}=\frac{e^{st}}{\left ( a+b\right ) \cosh \left ( a\sqrt{s}\right ) }\] The function \(\cosh \left ( x\right ) \) is zero at \(\pm \frac{i\pi }{2}+2i\pi n\) where \(n\) is the set of integers. For \(\cosh \left ( a\sqrt{s}\right ) \) this becomes \(-\frac{1}{4}\frac{\pi ^{2}}{a^{2}}\left ( 1+2n\right ) ^{2}\) for \(n\) integer. Hence, for \(n=0\)\begin{align*} res\left ( s\rightarrow \frac{-\pi ^{2}}{4a^{2}}\right ) & =\frac{1}{\left ( a+b\right ) }\lim _{s\rightarrow \frac{-\pi ^{2}}{4a^{2}}}\left ( s+\frac{\pi ^{2}}{4a^{2}}\right ) \frac{N\left ( s\right ) }{D^{\prime }\left ( s\right ) }\\ & =\frac{1}{\left ( a+b\right ) }\lim _{s\rightarrow \frac{-\pi ^{2}}{4a^{2}}}\frac{\left ( s+\frac{\pi ^{2}}{4a^{2}}\right ) 2\sqrt{s}e^{st}}{a\sinh \left ( a\sqrt{s}\right ) }\\ & =\frac{1}{\left ( a+b\right ) }\frac{\left ( 0\right ) 2\sqrt{\frac{-\pi ^{2}}{4a^{2}}}e^{\frac{-\pi ^{2}}{4a^{2}}t}}{a\sinh \left ( a\sqrt{\frac{-\pi ^{2}}{4a^{2}}}\right ) }\\ & =\frac{1}{\left ( a+b\right ) }\frac{\left ( 0\right ) 2\sqrt{\frac{-\pi ^{2}}{4a^{2}}}e^{\frac{-\pi ^{2}}{4a^{2}}t}}{a\sinh \left ( \frac{\pi i}{2}\right ) }\\ & =\frac{1}{\left ( a+b\right ) }\frac{\left ( 0\right ) 2\sqrt{\frac{-\pi ^{2}}{4a^{2}}}e^{\frac{-\pi ^{2}}{4a^{2}}t}}{ai}\\ & =0 \end{align*}
Hence the residue is zero. If we try for \(n=1,2,\cdots \) we’ll find all residues are zero. Hence\begin{align*} f\left ( t\right ) & =\frac{1}{2\pi i}\left ( 2\pi i\sum \limits _{i=1}^{poles}res\left ( s_{i}\right ) \right ) \\ & =0 \end{align*}
I have something wrong. Need more time to work on this.