Find the Fourier cosine and Fourier sin transforms of \(f\left ( t\right ) =te^{-at}\) for positive \(a\)
solution
\(f\left ( t\right ) \) is plotted in time domain to see what its shape using \(a=0.5\) for illustration
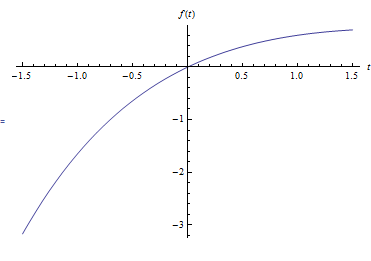
The Fourier cosine transform of \(f\left ( t\right ) \) is
\[ F_{c}\left ( \omega \right ) =\int _{0}^{\infty }f\left ( t\right ) \cos \left ( \omega t\right ) dt \]
\(f\left ( t\right ) \) is first verified that it is smooth and \(\int _{0}^{\infty }\left \vert f\left ( t\right ) \right \vert dt<\infty \) (i.e absolutely integrable function). \(f\left ( t\right ) \) is clearly smooth function since it is the product of two smooth functions. \(\int _{0}^{\infty }\left \vert f\left ( t\right ) \right \vert dt=\int _{0}^{\infty }\left \vert te^{-at}\right \vert dt=\int _{0}^{\infty }te^{-at}dt=\frac{1}{a^{2}}\), hence the integral converges. This means the Fourier cosine transform can be used. Evaluating \(F_{c}\left ( \omega \right ) .\)\[ F_{c}\left ( \omega \right ) =\int _{0}^{\infty }te^{-at}\cos \left ( \omega t\right ) dt \] Integration by parts 2 times in order to obtain the same original integral, Let \[ I=\int _{0}^{\infty }te^{-at}\cos \left ( \omega t\right ) dt \] Using \(\int udv=\left [ uv\right ] -\int vdu\), let \(u=te^{-at}\) and \(dv=\cos \left ( \omega t\right ) \), then \(du=e^{-at}-ate^{-at}\) and \(v=\int \cos \left ( \omega t\right ) dt=\frac{\sin \left ( \omega t\right ) }{\omega }\), hence\begin{align*} I & =\overbrace{\left [ te^{-at}\frac{\sin \left ( \omega t\right ) }{\omega }\right ] _{0}^{\infty }}^{0} -\int \frac{\sin \left ( \omega t\right ) }{\omega }\left ( e^{-at}-ate^{-at}\right ) dt\\ & =-\int \frac{\sin \left ( \omega t\right ) }{\omega }e^{-at}dt+\int \frac{\sin \left ( \omega t\right ) }{\omega }ate^{-at}dt\\ & =-\frac{1}{\omega }\int e^{-at}\sin \left ( \omega t\right ) dt+\frac{a}{\omega }\int te^{-at}\sin \left ( \omega t\right ) dt \end{align*}
\(\int e^{-at}\sin \left ( \omega t\right ) dt\) can be integrated by parts giving \(\frac{\omega }{a^{2}+\omega ^{2}}\). For the second term \(\int te^{-at}\sin \left ( \omega t\right ) dt\), integrating by parts again, but now let \(u=te^{-at}\) and \(dv=\sin \left ( \omega t\right ) \), then \(du=e^{-at}-ate^{-at}\) and \(v=\int \sin \left ( \omega t\right ) dt=\frac{-\cos \left ( \omega t\right ) }{\omega }\), hence the above becomes\begin{align*} I & =-\frac{1}{\omega }\left ( \frac{\omega }{a^{2}+\omega ^{2}}\right ) +\frac{a}{\omega }\left ( \overbrace{\left [ -te^{-at}\frac{\cos \left ( \omega t\right ) }{\omega }\right ] _{0}^{\infty }}^{0}-\int _{0}^{\infty }\frac{-\cos \left ( \omega t\right ) }{\omega }\left ( e^{-at}-ate^{-at}\right ) dt\right ) \\ & =-\frac{1}{\omega }\left ( \frac{\omega }{a^{2}+\omega ^{2}}\right ) +\frac{a}{\omega }\left ( \frac{1}{\omega }\int _{0}^{\infty }\cos \left ( \omega t\right ) \left ( e^{-at}-ate^{-at}\right ) dt\right ) \\ & =-\frac{1}{\omega }\left ( \frac{\omega }{a^{2}+\omega ^{2}}\right ) +\frac{a}{\omega ^{2}}\left ( \overbrace{\int _{0}^{\infty }\cos \left ( \omega t\right ) e^{-at}}^{\frac{a}{a^{2}+\omega ^{2}}} -a\overbrace{\int _{0}^{\infty }te^{-at}\cos \left ( \omega t\right ) dt}^{I} \right ) \end{align*}
The original integral \(I\) is obtained in the RHS. Solving for \(I\) and simplifying gives\begin{align*} I & =-\frac{1}{\omega }\left ( \frac{\omega }{a^{2}+\omega ^{2}}\right ) +\frac{a}{\omega ^{2}}\left ( \frac{a}{a^{2}+\omega ^{2}}-aI\right ) \\ & =-\left ( \frac{1}{a^{2}+\omega ^{2}}\right ) +\frac{a^{2}}{\omega ^{2}\left ( a^{2}+\omega ^{2}\right ) }-\frac{a^{2}I}{\omega ^{2}}\\ I+\frac{a^{2}I}{\omega ^{2}} & =\frac{-1}{a^{2}+\omega ^{2}}+\frac{a^{2}}{\omega ^{2}\left ( a^{2}+\omega ^{2}\right ) }\\ I\left ( \frac{\omega ^{2}+a^{2}}{\omega ^{2}}\right ) & =\frac{-\omega ^{2}+a^{2}}{\omega ^{2}\left ( a^{2}+\omega ^{2}\right ) }\\ I & =\frac{\frac{\left ( a^{2}-\omega ^{2}\right ) }{\omega ^{2}\left ( a^{2}+\omega ^{2}\right ) }}{\left ( \frac{\omega ^{2}+a^{2}}{\omega ^{2}}\right ) }\\ I & =\frac{\left ( a^{2}-\omega ^{2}\right ) \omega ^{2}}{\omega ^{2}\left ( a^{2}+\omega ^{2}\right ) \left ( \omega ^{2}+a^{2}\right ) } \end{align*}
Therefore\[ I=F_{c}\left ( \omega \right ) =\frac{\left ( a^{2}-\omega ^{2}\right ) }{\left ( a^{2}+\omega ^{2}\right ) ^{2}}\]
From the definition, the Fourier sin transform of \(f\left ( t\right ) \) is\[ F_{s}\left ( \omega \right ) =\int _{0}^{\infty }te^{-at}\sin \left ( \omega t\right ) dt \] This can be integrated by parts 2 times in order to obtain the same integral we started with. Let \[ I=\int _{0}^{\infty }te^{-at}\sin \left ( \omega t\right ) dt \] Using \(\int udv=\left [ uv\right ] -\int vdu\), let \(u=te^{-at}\) and \(dv=\sin \left ( \omega t\right ) \), then \(du=e^{-at}-ate^{-at}\) and \(v=\int \sin \left ( \omega t\right ) dt=-\frac{\cos \left ( \omega t\right ) }{\omega }\), hence\begin{align*} I & =\overbrace{\left [ -te^{-at}\frac{\cos \left ( \omega t\right ) }{\omega }\right ] _{0}^{\infty }}^{0} +\int \frac{\cos \left ( \omega t\right ) }{\omega }\left ( e^{-at}-ate^{-at}\right ) dt\\ & =\int \frac{\cos \left ( \omega t\right ) }{\omega }e^{-at}dt-\int \frac{\cos \left ( \omega t\right ) }{\omega }ate^{-at}dt\\ & =\frac{1}{\omega }\int e^{-at}\cos \left ( \omega t\right ) dt-\frac{a}{\omega }\int te^{-at}\cos \left ( \omega t\right ) dt \end{align*}
\(\int e^{-at}\cos \left ( \omega t\right ) dt\) can be integrated by parts giving \(\frac{a}{a^{2}+\omega ^{2}}\). For the second term \(\int te^{-at}\cos \left ( \omega t\right ) dt\), integrating by parts again, but now let \(u=te^{-at}\) and \(dv=\cos \left ( \omega t\right ) \), then \(du=e^{-at}-ate^{-at}\) and \(v=\int \cos \left ( \omega t\right ) dt=\frac{\sin \left ( \omega t\right ) }{\omega }\), hence the above becomes\begin{align*} I & =\frac{1}{\omega }\left ( \frac{a}{a^{2}+\omega ^{2}}\right ) -\frac{a}{\omega }\left ( \overbrace{\left [ te^{-at}\frac{\sin \left ( \omega t\right ) }{\omega }\right ] _{0}^{\infty }}^{0} -\int _{0}^{\infty }\frac{\sin \left ( \omega t\right ) }{\omega }\left ( e^{-at}-ate^{-at}\right ) dt\right ) \\ & =\frac{1}{\omega }\left ( \frac{a}{a^{2}+\omega ^{2}}\right ) +\frac{a}{\omega }\left ( \frac{1}{\omega }\int _{0}^{\infty }\sin \left ( \omega t\right ) \left ( e^{-at}-ate^{-at}\right ) dt\right ) \\ & =\frac{1}{\omega }\left ( \frac{a}{a^{2}+\omega ^{2}}\right ) +\frac{a}{\omega ^{2}}\left ( \overbrace{\int _{0}^{\infty }\sin \left ( \omega t\right ) e^{-at}} ^{\frac{\omega }{a^{2}+\omega ^{2}}} -a\overbrace{\int _{0}^{\infty }te^{-at}\sin \left ( \omega t\right ) dt}^{I}\right ) \end{align*}
The original integral \(I\) appeared again in the RHS. Solving for \(I\) and simplifying gives\begin{align*} I & =\frac{1}{\omega }\left ( \frac{a}{a^{2}+\omega ^{2}}\right ) +\frac{a}{\omega ^{2}}\left ( \frac{\omega }{a^{2}+\omega ^{2}}-aI\right ) \\ & =\frac{a}{\omega \left ( a^{2}+\omega ^{2}\right ) }+\frac{a\omega }{\omega ^{2}\left ( a^{2}+\omega ^{2}\right ) }-\frac{a^{2}I}{\omega ^{2}}\\ I+\frac{a^{2}I}{\omega ^{2}} & =\frac{a}{\omega \left ( a^{2}+\omega ^{2}\right ) }+\frac{a}{\omega \left ( a^{2}+\omega ^{2}\right ) }\\ I\left ( \frac{\omega ^{2}+a^{2}}{\omega ^{2}}\right ) & =\frac{2a}{\omega \left ( a^{2}+\omega ^{2}\right ) }\\ I & =\frac{\frac{2a}{\omega \left ( a^{2}+\omega ^{2}\right ) }}{\left ( \frac{\omega ^{2}+a^{2}}{\omega ^{2}}\right ) }\\ I & =\frac{2a\omega ^{2}}{\omega \left ( a^{2}+\omega ^{2}\right ) \left ( \omega ^{2}+a^{2}\right ) } \end{align*}
Therefore\[ I=F_{s}\left ( \omega \right ) =\frac{2a\omega }{\left ( a^{2}+\omega ^{2}\right ) ^{2}}\]
Find the inverse Fourier transform of \(F\left ( \omega \right ) =\frac{1-e^{-2i\omega }}{-\omega ^{2}+4i\omega +3}\)
solution:
Using the following definitions\begin{align*} f\left ( t\right ) & =\frac{1}{2\pi }\int _{-\infty }^{\infty }F\left ( \omega \right ) e^{i\omega t}d\omega \\ F\left ( \omega \right ) & =\int _{-\infty }^{\infty }f\left ( t\right ) e^{-i\omega t}dt \end{align*}
Now\begin{align*} F\left ( \omega \right ) & =\frac{1-e^{-2i\omega }}{-\omega ^{2}+4i\omega +3}=\frac{1-e^{-2i\omega }}{-\left ( \omega ^{2}-4i\omega -3\right ) }=\frac{1-e^{-2i\omega }}{-\left ( \omega -3i\right ) \left ( \omega -i\right ) }\\ & =\frac{e^{-2i\omega }-1}{\left ( \omega -3i\right ) \left ( \omega -i\right ) } \end{align*}
Let\[ \frac{1}{\left ( \omega -3i\right ) \left ( \omega -i\right ) }=\frac{A}{\left ( \omega -3i\right ) }+\frac{B}{\left ( \omega -i\right ) }\] Hence \[ A=\lim _{\omega \rightarrow 3i}\frac{1}{\left ( \omega -i\right ) }=\frac{1}{2i}=\frac{-i}{2}\] And\[ B=\lim _{\omega \rightarrow i}\frac{1}{\left ( \omega -3i\right ) }=\frac{1}{-2i}=\frac{i}{2}\] Hence\[ \frac{1}{\left ( \omega -3i\right ) \left ( \omega -i\right ) }=\frac{1}{2}\frac{-i}{\left ( \omega -3i\right ) }+\frac{1}{2}\frac{i}{\left ( \omega -i\right ) }\]\begin{align*} \frac{e^{-2i\omega }-1}{\left ( \omega -3i\right ) \left ( \omega -i\right ) } & =\left ( \frac{-ie^{-2i\omega }}{2\left ( \omega -3i\right ) }+\frac{1}{2}\frac{ie^{-2i\omega }}{\left ( \omega -i\right ) }\right ) -\left ( \frac{1}{2}\frac{-i}{\left ( \omega -3i\right ) }+\frac{1}{2}\frac{i}{\left ( \omega -i\right ) }\right ) \\ & =\frac{-i}{2}\frac{e^{-2i\omega }}{\left ( \omega -3i\right ) }+\frac{i}{2}\frac{e^{-2i\omega }}{\left ( \omega -i\right ) }+\frac{i}{2}\frac{1}{\left ( \omega -3i\right ) }-\frac{i}{2}\frac{1}{\left ( \omega -i\right ) }\\ & =\frac{1}{2}\frac{e^{-2i\omega }}{\left ( i\omega +3\right ) }-\frac{1}{2}\frac{e^{-2i\omega }}{\left ( i\omega +1\right ) }-\frac{1}{2}\frac{1}{\left ( i\omega +3\right ) }+\frac{1}{2}\frac{1}{\left ( i\omega +1\right ) } \end{align*}
From table, \[ H\left ( t\right ) e^{-\alpha t}\iff \frac{1}{i\omega +\alpha }\] And\[ H\left ( t-t_{0}\right ) f\left ( t-t_{0}\right ) \iff e^{-i\omega t_{0}}F\left ( \omega \right ) \] Hence, using the above two relations we now find the inverse Fourier transform\begin{align*} F^{-1}\left ( \frac{e^{-2i\omega }-1}{\left ( \omega -3i\right ) \left ( \omega -i\right ) }\right ) & =H\left ( t-2\right ) \frac{1}{2}e^{-3\left ( t-2\right ) }-H\left ( t-2\right ) \frac{1}{2}e^{-\left ( t-2\right ) }-H\left ( t\right ) \frac{1}{2}e^{-3t}+H\left ( t\right ) \frac{1}{2}e^{-t}\\ & =\frac{1}{2}H\left ( t-2\right ) \left ( e^{-3t+6}-e^{-t+2}\right ) +\frac{1}{2}H\left ( t\right ) \left ( e^{-t}-e^{-3t}\right ) \end{align*}
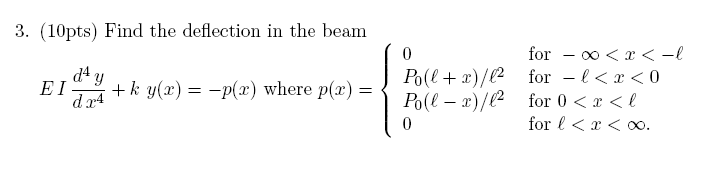
Solution:
Method overview: Load \(p\left ( x\right ) \) is expressed in the Fourier transform space \(\omega \). The LHS is also converted to Fourier transform space. \(Y\left ( \omega \right ) \) is then solved for algebraically. The inverse Fourier transform is used to obtain \(y\left ( t\right ) \), the solution.
Plotting the load \(p\left ( x\right ) \) for some values, in order to see its shape (let \(L=1\), \(P_{0}=1\)), gives the following
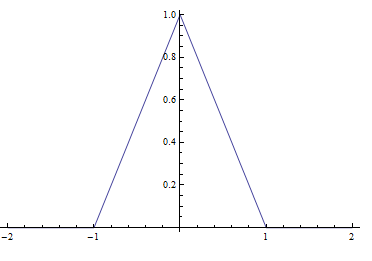
\(p\left ( x\right ) \) is an even function. Assuming simply supported beam, symmetry of load implies that the deflection will also be even. Hence an even function for a solution is assumed and the \(\cos \) Fourier transform is therefore used.\[ y\left ( x\right ) =\frac{2}{\pi }\int _{0}^{\infty }Y\cos \left ( \omega x\right ) d\omega \] where \(Y\equiv Y\left ( \omega \right ) \) is the Fourier transform on \(y\left ( x\right ) \) to be found. Taking \(4^{th}\) derivative w.r.t. \(x\) gives\[ y^{\left ( 4\right ) }\left ( x\right ) =\frac{2}{\pi }\int _{0}^{\infty }\omega ^{4}Y\cos \left ( \omega x\right ) d\omega \] The load \(p\left ( x\right ) \) is \begin{equation} p\left ( x\right ) =\frac{2}{\pi }\int _{0}^{\infty }P\left ( \omega \right ) \cos \left ( \omega x\right ) d\omega \tag{1} \end{equation} Where \(P\left ( \omega \right ) \) is the Fourier transform of \(p\left ( x\right ) \). \(P\left ( \omega \right ) \) can be found since \(p\left ( x\right ) \) is given\begin{align} P\left ( \omega \right ) & =\int _{0}^{\infty }p\left ( x\right ) \cos \left ( \omega x\right ) dx\nonumber \\ & =\int _{0}^{L}\frac{P_{0}\left ( L-x\right ) }{L^{2}}\cos \left ( \omega x\right ) dx\nonumber \\ & =\int _{0}^{L}\frac{P_{0}}{L}\cos \left ( \omega x\right ) dx-\frac{P_{0}}{L^{2}}x\cos \left ( \omega x\right ) dx\nonumber \\ & =\frac{P_{0}}{L}\left [ \frac{\sin \left ( \omega x\right ) }{\omega }\right ] _{0}^{L}-\frac{P_{0}}{L^{2}}\int _{0}^{L}x\cos \left ( \omega x\right ) dx \tag{2} \end{align}
Solving \(\int _{0}^{L}x\cos \left ( \omega x\right ) dx\), by integration by parts. Using \(\int udv=\left [ uv\right ] -\int vdu\), let \(u=x\) and \(dv=\cos \left ( \omega t\right ) \), then \(du=1\) and \(v=\int \cos \left ( \omega x\right ) dx=\frac{\sin \left ( \omega x\right ) }{\omega }\), hence\begin{align*} \int _{0}^{L}x\cos \left ( \omega x\right ) dx & =\left [ x\frac{\sin \left ( \omega x\right ) }{\omega }\right ] _{0}^{L}-\int _{0}^{L}\frac{\sin \left ( \omega x\right ) }{\omega }dx\\ & =\frac{L}{\omega }\sin \left ( \omega L\right ) -\frac{1}{\omega }\left [ \frac{-\cos \left ( \omega x\right ) }{\omega }\right ] _{0}^{L}\\ & =\frac{L}{\omega }\sin \left ( \omega L\right ) +\frac{1}{\omega ^{2}}\left ( \cos \left ( \omega L\right ) -1\right ) \end{align*}
Substituting the above in Eq. (2) results in\begin{align*} P\left ( \omega \right ) & =\frac{P_{0}}{L}\frac{\sin \left ( \omega L\right ) }{\omega }-\frac{P_{0}}{L^{2}}\left ( \frac{L}{\omega }\sin \left ( \omega L\right ) +\frac{1}{\omega ^{2}}\left ( \cos \left ( \omega L\right ) -1\right ) \right ) \\ & =\frac{P_{0}}{\omega L}\sin \left ( \omega L\right ) -\frac{P_{0}}{\omega L}\sin \left ( \omega L\right ) -\frac{P_{0}}{\omega ^{2}L^{2}}\left ( \cos \left ( \omega L\right ) -1\right ) \\ & =-\frac{P_{0}}{\omega ^{2}L^{2}}\left ( \cos \left ( \omega L\right ) -1\right ) \end{align*}
Substituting the above in Eq. (1) gives\[ p\left ( x\right ) =\frac{-2}{\pi }\int _{0}^{\infty }\frac{P_{0}}{\omega ^{2}L^{2}}\left ( \cos \left ( \omega L\right ) -1\right ) \cos \left ( \omega x\right ) d\omega \] Therefore, the original ODE now becomes\begin{align*} EIy^{\left ( 4\right ) }\left ( x\right ) +ky\left ( x\right ) & =p\left ( x\right ) \\ EI\frac{2}{\pi }\int _{0}^{\infty }\omega ^{4}Y\cos \left ( \omega x\right ) d\omega +k\frac{2}{\pi }\int _{0}^{\infty }Y\cos \left ( \omega x\right ) d\omega & =\frac{-2}{\pi }\int _{0}^{\infty }\frac{P_{0}}{\omega ^{2}L^{2}}\left ( \cos \left ( \omega L\right ) -1\right ) \cos \left ( \omega x\right ) d\omega \end{align*}
Hence\[ \frac{2}{\pi }\int _{0}^{\infty }\left [ EI\omega ^{4}Y+kY+\frac{P_{0}}{\omega ^{2}L^{2}}\left ( \cos \left ( \omega L\right ) -1\right ) \right ] \cos \left ( \omega x\right ) d\omega =0 \] Since the integral is zero, and \(\cos \left ( \omega x\right ) \neq 0\), then it must be that\[ EI\omega ^{4}Y+kY+\frac{P_{0}}{\omega ^{2}L^{2}}\left ( \cos \left ( \omega L\right ) -1\right ) =0 \] Solving for \(Y\) from the above gives\begin{align*} Y\left ( EI\omega ^{4}+k\right ) & =-\frac{P_{0}}{\omega ^{2}L^{2}}\cos \left ( \omega L\right ) +\frac{P_{0}}{\omega ^{2}L^{2}}\\ Y & =\frac{-P_{0}}{L^{2}}\frac{\cos \left ( \omega L\right ) }{EI\omega ^{6}+\omega ^{2}k}+\frac{P_{0}}{L^{2}}\frac{1}{EI\omega ^{6}+\omega ^{2}k} \end{align*}
Taking the inverse Fourier cosine transform in order to find \(y\left ( x\right ) \)\begin{align*} y\left ( x\right ) & =\frac{1}{2\pi }\int _{0}^{\infty }\left ( \frac{-P_{0}}{L^{2}}\frac{\cos \left ( \omega L\right ) }{EI\omega ^{6}+\omega ^{2}k}+\frac{P_{0}}{L^{2}}\frac{1}{EI\omega ^{6}+\omega ^{2}k}\right ) \cos \left ( \omega x\right ) d\omega \\ & =\frac{-1}{2\pi }\frac{P_{0}}{L^{2}}\int _{0}^{\infty }\frac{\cos \left ( \omega L\right ) \cos \left ( \omega x\right ) }{EI\omega ^{6}+\omega ^{2}k}d\omega +\frac{1}{2\pi }\frac{P_{0}}{L^{2}}\int _{0}^{\infty }\frac{\cos \left ( \omega x\right ) }{EI\omega ^{6}+\omega ^{2}k}d\omega \end{align*}
The final step to compute the above was not required to do per class announcement.
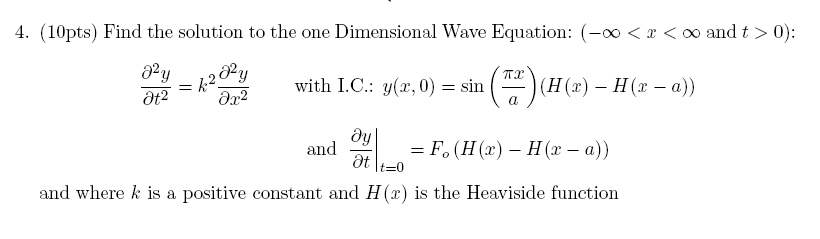
Solution
Method review: Laplace transform is used to obtain a differential equation in \(Y\left ( x,s\right ) \). Then Fourier transform is used to obtain an algebraic equation in \(Y\left ( \omega ,s\right ) \). The inverse Laplace transform is used to obtain \(Y\left ( \omega ,t\right ) \) and finally the inverse Fourier transform is used to obtain \(y\left ( x,t\right ) .\)Let \[ f\left ( x\right ) =y\left ( x,0\right ) =\sin \left ( \frac{\pi x}{a}\right ) \left ( H\left ( x\right ) -H\left ( x-a\right ) \right ) \] And let its Fourier transform be\[ F\left ( \omega \right ) =\mathcal{F}\left ( f\left ( x\right ) \right ) =\int _{0}^{a}\sin \left ( \frac{\pi x}{a}\right ) e^{-i\omega x}dx=\frac{a\left ( 1+e^{-ia\omega }\right ) \pi }{\pi ^{2}-a^{2}\omega ^{2}}\] And let\[ g\left ( x\right ) =y^{\prime }\left ( x,0\right ) =F_{0}\left ( H\left ( x\right ) -H\left ( x-a\right ) \right ) \] And let its Fourier transform be\[ G\left ( \omega \right ) =\mathcal{F}\left ( y^{\prime }\left ( x,0\right ) \right ) =\int _{0}^{a}F_{0}e^{-i\omega x}dx=F_{0}\left [ \frac{e^{-i\omega x}}{-i\omega }\right ] _{0}^{a}=\frac{F_{0}}{-i\omega }\left ( e^{-i\omega a}-1\right ) =\frac{iF_{0}}{\omega }\left ( e^{-i\omega a}-1\right ) \] Now, taking the Laplace transform of the PDE gives\begin{align} s^{2}Y\left ( x,s\right ) -sy\left ( x,0\right ) -y^{\prime }\left ( x,0\right ) & =k^{2}\frac{d^{2}Y\left ( x,s\right ) }{dx^{2}}\nonumber \\ s^{2}Y\left ( x,s\right ) -sf\left ( x\right ) -g\left ( x\right ) & =k^{2}\frac{d^{2}Y\left ( x,s\right ) }{dx^{2}} \tag{1} \end{align}
Taking the Fourier transform of the above equation. The following relation is used \(\frac{d^{n}y\left ( x\right ) }{dx^{n}}\Longleftrightarrow \left ( i\omega \right ) ^{n}Y\left ( \omega \right ) \), hence \(\frac{d^{2}y\left ( x\right ) }{dx^{2}}\Longleftrightarrow -\omega ^{2}Y\left ( \omega \right ) \) hence\[ s^{2}Y\left ( \omega ,s\right ) -sF\left ( \omega \right ) -G\left ( \omega \right ) =-k^{2}\omega ^{2}Y\left ( \omega \right ) \] Solving for \(Y\left ( \omega ,s\right ) \) gives\begin{align} Y\left ( \omega ,s\right ) & =\frac{sF\left ( \omega \right ) +G\left ( \omega \right ) }{\left ( s^{2}+k^{2}\omega ^{2}\right ) }\nonumber \\ & =F\left ( \omega \right ) \frac{s}{s^{2}+k^{2}\omega ^{2}}+G\left ( \omega \right ) \frac{1}{s^{2}+k^{2}\omega ^{2}} \tag{2} \end{align}
Taking inverse Laplace transform of \(\frac{s}{s^{2}+k^{2}\omega ^{2}}.\)Using \(\frac{s}{\left ( s^{2}+a^{2}\right ) }\Longleftrightarrow \cos \left ( at\right ) \), hence \(\frac{s}{s^{2}+k^{2}\omega ^{2}}\Longleftrightarrow \cos \left ( k\omega t\right ) .\) Taking inverse Laplace transform of \(\frac{1}{s^{2}+k^{2}\omega ^{2}},\) from \(\frac{a}{\left ( s^{2}+a^{2}\right ) }\Longleftrightarrow \sin \left ( at\right ) \), hence \(\frac{1}{k\omega }\frac{1}{s^{2}+k^{2}\omega ^{2}}\Longleftrightarrow \frac{\sin \left ( k\omega t\right ) }{k\omega }\)
Therefore inverse Laplace of Eq. (2) is \begin{equation} Y\left ( \omega ,t\right ) =F\left ( \omega \right ) \cos \left ( k\omega t\right ) +G\left ( \omega \right ) \frac{\sin \left ( k\omega t\right ) }{k\omega }\tag{3} \end{equation} Taking the inverse Fourier transform of the above. Writing \(\cos \left ( k\omega t\right ) =\frac{e^{ik\omega t}+e^{-ik\omega t}}{2}\) and \(\sin \left ( k\omega t\right ) =\frac{e^{ik\omega t}-e^{-ik\omega t}}{2i}\) and applying the definition of inverse Fourier transform, results in\begin{align*} y\left ( x,t\right ) & =\frac{1}{2\pi }\int \limits _{-\infty }^{\infty }e^{i\omega x}\left ( F\left ( \omega \right ) \cos \left ( k\omega t\right ) +G\left ( \omega \right ) \frac{\sin \left ( k\omega t\right ) }{k\omega }\right ) d\omega \\ & =\frac{1}{2\pi }\int \limits _{-\infty }^{\infty }e^{i\omega x}\left ( F\left ( \omega \right ) \frac{e^{ik\omega t}+e^{-ik\omega t}}{2}+\frac{G\left ( \omega \right ) }{k\omega }\frac{e^{ik\omega t}-e^{-ik\omega t}}{2i}\right ) d\omega \\ & =\frac{1}{4\pi }\int \limits _{-\infty }^{\infty }F\left ( \omega \right ) \left ( e^{i\left ( x+kt\right ) \omega }+e^{i\left ( x-kt\right ) \omega }\right ) d\omega +\frac{1}{4\pi }\int \limits _{-\infty }^{\infty }\frac{G\left ( \omega \right ) }{ik\omega }\left ( e^{i\left ( x+kt\right ) \omega }-e^{i\left ( x-kt\right ) \omega }\right ) d\omega \end{align*}
Hence, breaking the above into 4 integrals gives\begin{align*} y\left ( x,t\right ) & =\frac{1}{2}\left ( \overbrace{\frac{1}{2\pi }\int \limits _{-\infty }^{\infty }F\left ( \omega \right ) e^{i\left ( x+kt\right ) \omega }d\omega }^{f\left ( x+kt\right ) }\right ) +\frac{1}{2}\left ( \overbrace{\frac{1}{2\pi }\int \limits _{-\infty }^{\infty }F\left ( \omega \right ) e^{i\left ( x-kt\right ) \omega }d\omega }^{f\left ( x-kt\right ) }\right ) \\ & +\frac{1}{2k}\left ( \frac{1}{2\pi }\int \limits _{-\infty }^{\infty }G\left ( \omega \right ) \frac{e^{i\left ( x+kt\right ) \omega }}{i\omega }d\omega -\frac{1}{2\pi }\int \limits _{-\infty }^{\infty }G\left ( \omega \right ) \frac{e^{i\left ( x-kt\right ) \omega }}{i\omega }d\omega \right ) \end{align*}
Or\begin{align*} y\left ( x,t\right ) & =\frac{1}{2}f\left ( x+kt\right ) +\frac{1}{2}f\left ( x-kt\right ) +\frac{1}{2k}\left ( \frac{1}{2\pi }\int \limits _{-\infty }^{\infty }G\left ( \omega \right ) \frac{e^{i\left ( x+kt\right ) \omega }-e^{i\left ( x-kt\right ) \omega }}{i\omega }d\omega \right ) \\ & =\frac{1}{2}f\left ( x+kt\right ) +\frac{1}{2}f\left ( x-kt\right ) +\frac{1}{2k}\left ( \int \limits _{x-kt}^{x+kt} \overbrace{\left ( \frac{1}{2\pi }\int \limits _{-\infty }^{\infty }G\left ( \omega \right ) e^{i\xi \omega }d\omega \right ) }^{g\left ( \xi \right ) } d\xi \right ) \\ & =\frac{1}{2}f\left ( x+kt\right ) +\frac{1}{2}f\left ( x-kt\right ) +\frac{1}{2k}\int \limits _{x-kt}^{x+kt}g\left ( \xi \right ) d\xi \end{align*}
Where \[ g\left ( \xi \right ) =F_{0}\left ( H\left ( \xi \right ) -H\left ( \xi -a\right ) \right ) \] Hence the final solution is\begin{align*} y\left ( x,t\right ) & =\frac{1}{2}f\left ( x+kt\right ) +\frac{1}{2}f\left ( x-kt\right ) +\frac{1}{2k}\int \limits _{x-kt}^{x+kt}F_{0}\left ( H\left ( \xi \right ) -H\left ( \xi -a\right ) \right ) d\xi \\ & =\frac{1}{2}\sin \left ( \frac{\pi \left ( x+kt\right ) }{a}\right ) \left ( H\left ( x+kt\right ) -H\left ( x+kt-a\right ) \right ) \\ & +\frac{1}{2}\sin \left ( \frac{\pi \left ( x-kt\right ) }{a}\right ) \left ( H\left ( x-kt\right ) -H\left ( x-kt-a\right ) \right ) \\ & +\frac{1}{2k}\int \limits _{x-kt}^{x+kt}F_{0}\left ( H\left ( \xi \right ) -H\left ( \xi -a\right ) \right ) d\xi \end{align*}
But \[ \int \limits _{x-kt}^{x+kt}F_{0}\left ( H\left ( \xi \right ) -H\left ( \xi -a\right ) \right ) d\xi =F_{0}\int \limits _{x-kt}^{x+kt}H\left ( \xi \right ) d\xi -F_{0}\int \limits _{x-kt}^{x+kt}H\left ( \xi -a\right ) d\xi \] Hence\[ F_{0}\int \limits _{x-kt}^{x+kt}H\left ( \xi \right ) d\xi -F_{0}\int \limits _{x-kt}^{x+kt}H\left ( \xi -a\right ) d\xi =F_{0}\left ( \left ( x+kt\right ) -\left ( x-kt\right ) \right ) =\begin{array} [c]{ccc}2F_{0}kt & & 0<x-kt\text{ and }x+kt<a\\ 0 & & otherwise \end{array} \] Hence, for \(0<x-kt\) and \(x+kt<a\,\), the solution is\begin{align*} y\left ( x,t\right ) & =\frac{1}{2}\left ( \sin \left ( \frac{\pi \left ( x+kt\right ) }{a}\right ) \left ( H\left ( x+kt\right ) -H\left ( x+kt-a\right ) \right ) +\sin \left ( \frac{\pi \left ( x-kt\right ) }{a}\right ) \left ( H\left ( x-kt\right ) -H\left ( x-kt-a\right ) \right ) \right ) \\ & +2F_{0}kt \end{align*}
Otherwise, the solution is\[ y\left ( x,t\right ) =\frac{1}{2}\left ( \sin \left ( \frac{\pi \left ( x+kt\right ) }{a}\right ) \left ( H\left ( x+kt\right ) -H\left ( x+kt-a\right ) \right ) +\sin \left ( \frac{\pi \left ( x-kt\right ) }{a}\right ) \left ( H\left ( x-kt\right ) -H\left ( x-kt-a\right ) \right ) \right ) \]