
Problem: Prove or disprove this assertion: if \(f\) is differentiable at \(x\), then for any \(\alpha \neq 1\)
\[ f^{\prime }\relax (x) =\lim _{h\rightarrow 0}\frac {f\left (x+h\right ) -f\left (x+\alpha h\right ) }{h-\alpha h}\]
Solution:
Since \(f^{\prime }\relax (x) \) exists, then expanding \(f\left ( x+h\right ) \) and \(f\left (x+\alpha h\right ) \) in Taylor series results in
\begin {align*} f\left (x+h\right ) & =f\relax (x) +f^{\prime }\relax (x) h+\cdots \text {(Higher\ Order\ Terms\ involving\ }h^{m}\text { where }m\geq 2\text {)}\\ f\left (x+\alpha h\right ) & =f\relax (x) +\left (\alpha h\right ) f^{\prime }\relax (x) +\cdots \text {(Higher\ Order\ Terms\ involving\ }\left (\alpha h\right ) ^{m}\text { where }m\geq 2\text {)} \end {align*}
From first equation above we write
\begin {equation} f\relax (x) =f\left (x+h\right ) -hf^{^{\prime }}\relax (x) -(\text {Higher\ Order\ Terms\ involving\ }h^{m}\text {where }m\geq 2) \tag {1} \end {equation}
And from the second equation we write
\begin {equation} f\relax (x) =f\left (x+\alpha h\right ) -\left (\alpha h\right ) f^{^{\prime }}\relax (x) -(\text {Higher\ Order\ Terms\ involving\ }\left (\alpha h\right ) ^{m}\ \text {where }m\geq 2) \tag {2} \end {equation}
equating equations (1)-(2)=0 we obtain
\begin {align*} \left [ f\left (x+h\right ) -hf^{^{\prime }}\relax (x) -O\left ( \ h^{m}\right ) \right ] -\left [ f\left (x+\alpha h\right ) -\left (\alpha h\right ) f^{^{\prime }}\relax (x) -O\ \left (\alpha h\right ) ^{m}\right ] & =0\\ f^{\prime }\relax (x) \left [ \alpha h-h\right ] +f\left (x+h\right ) -f\left (x+\alpha h\right ) -O\ \left (h^{m}\right ) +O\left (\alpha h\right ) ^{m} & =0 \end {align*}
Keep \(f^{\prime }\relax (x) \) on one side, and move everything to the other side results in
\[ f^{\prime }\relax (x) =\frac {f\left (x+\alpha h\right ) -f\left ( x+h\right ) }{\left (\alpha h-h\right ) }+\frac {\left (O\ \left ( h^{m}\right ) -O\left (\alpha h\right ) ^{m}\right ) }{\left (\alpha h-h\right ) }\]
As \(h\) goes to zero the above reduces to
\[ f^{\prime }\relax (x) =\lim _{h\rightarrow 0}\frac {f\left (x+\alpha h\right ) -f\left (x+h\right ) }{\left (\alpha h-h\right ) }\]
rearrange the sign results in
\[ f^{\prime }\relax (x) =\lim _{h\rightarrow 0}\frac {f\left (x+h\right ) -f\left (x+\alpha h\right ) }{\left (h-\alpha h\right ) }\]
Problem: If the series for \(\ln x\) is truncated after the term involving \(\left (x-1\right ) ^{1000}\) and is then used to compute \(\ln 2\), what bound on the error can be give?
Answer:
Assume \(\ln x\) has a power series expansion around \(x_{0}\), we write, from definition of power series
\begin {equation} \ln \relax (x) =a_{0}+a_{1}\left (x-x_{0}\right ) +a_{2}\left ( x-x_{0}\right ) ^{2}+a_{3}\left (x-x_{0}\right ) ^{3}+\cdots +a_{n}\left ( x-x_{0}\right ) ^{n}+\cdots \tag {1} \end {equation}
When \(x_{0}=1\) we get
\begin {equation} \ln \relax (x) =a_{0}+a_{1}\left (x-1\right ) +a_{2}\left (x-1\right ) ^{2}+a_{3}\left (x-1\right ) ^{3}+\cdots +a_{n}\left (x-1\right ) ^{n}+\cdots \tag {2} \end {equation}
At \(x=1\) we obtain \(a_{0}=0\) since \(\ln \relax (1) =0\)
Differentiate (2)
\begin {equation} \frac {1}{x}=a_{1}+2a_{2}\left (x-1\right ) +3a_{3}\left (x-1\right ) ^{2}+\cdots +na_{n}\left (x-1\right ) ^{n-1}+\cdots \tag {3} \end {equation}
At \(x=1\) we obtain \(a_{1}=1\)
Differentiate (3)
\begin {equation} \frac {-1}{x^{2}}=2a_{2}+\left (3\times 2\right ) a_{3}\left (x-1\right ) +\cdots +n\left (n-1\right ) a_{n}\left (x-1\right ) ^{n-2}+\cdots \tag {4} \end {equation}
At \(x=1\) we obtain \(-1=2a_{2}\rightarrow a_{2}=\frac {-1}{2}\)
Differentiate (4)
\begin {equation} \frac {2}{x^{3}}=\left (3\times 2\right ) a_{3}+\cdots +n\left (n-1\right ) \left (n-2\right ) a_{n}\left (x-1\right ) ^{n-3}+\cdots \tag {5} \end {equation}
at \(x=1\) we obtain \(a_{3}=\frac {1}{3}\)
continue as above, we obtain the power series for \(\ln \relax (x) \) as
\[ \ln \relax (x) =\left (x-1\right ) -\frac {1}{2}\left (x-1\right ) ^{2}+\frac {1}{3}\left (x-1\right ) ^{3}-\frac {1}{4}\left (x-1\right ) ^{4}+\cdots +\frac {\left (-1\right ) ^{n+1}}{n}\left (x-1\right ) ^{n}+\cdots \]
Notice that for the above to converge, we need to have \(\left (x-1\right ) \leq 1\), or \(x\leq 2\)
Now if the series is truncated after \(\left (x-1\right ) ^{1000}\), hence \(n=1000\), and the maximum error will be the \(\left (n+1\right ) \) term.
Hence \begin {align*} E & \leq \left \vert \frac {\left (-1\right ) ^{1002}}{1001}\left ( x-1\right ) ^{1001}\right \vert \\ & \leq \frac {\left (x-1\right ) ^{1001}}{1001} \end {align*}
which for \(x=2\)
\begin {align*} E & \leq \frac {\left (2-1\right ) ^{1001}}{1001}\\ & \leq \frac {1}{1001}\\ & \leq 9.\,\allowbreak 99\times 10^{-4} \end {align*}
Problem: For small values of \(x\), how good is the approximation for \(\cos x\approx 1-\frac {1}{2}x^{2}\)? for what range of values will this approximation give correct results rounded to 3 decimal places?
Answer:
Expand \(\cos \relax (x) \) in power series, we write
\[ \cos \relax (x) =a_{0}+a_{1}\left (x-x_{0}\right ) +a_{2}\left ( x-x_{0}\right ) ^{2}+a_{3}\left (x-x_{0}\right ) ^{3}+\cdots +a_{n}\left ( x-x_{0}\right ) ^{n}+\cdots \]
expand at \(x_{0}=0\)
\[ \cos \relax (x) =a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+\cdots +a_{n}x^{n}+\cdots \]
At \(x=0\rightarrow a_{0}=1\), Differentiate the above
\[ -\sin \relax (x) =a_{1}+2a_{2}x+3a_{3}x^{2}+\cdots +na_{n}x^{n-1}+\cdots \]
at \(x=0\rightarrow a_{1}=0\), Differentiate the above
\[ -\cos \relax (x) =2a_{2}+\left (3\times 2\right ) a_{3}x+\cdots +n\left ( n-1\right ) a_{n}x^{n-2}+\cdots \]
at \(x=0\rightarrow a_{2}=-\frac {1}{2}\), continue as above, we obtain the series for \(\cos \relax (x) \) as
\[ \cos \relax (x) =1-\frac {1}{2}x^{2}+\frac {1}{4!}x^{4}-\cdots +\frac {\left (-1\right ) ^{n+1}}{n!}x^{n}+\cdots \]
Hence if we truncate the series at \(\cos \relax (x) \approx 1-\frac {1}{2}x^{2}\), then the maximum error will be bounded by \[ E\leq \frac {1}{4!}x^{4}\]
Since we want the error to be correct to 3 decimal places, then we write
\[ E<0.001 \]
Hence \begin {align*} x^{4} & <4!(0.001)\\ & <0.024 \end {align*}
Hence \[ x<\left (0.024\right ) ^{\frac {1}{4}}=0.393\,60 \]
So for \(x<0.393\,60\) radians (about \(22.\,\allowbreak 552^{0}\)), the approximation \(\cos \relax (x) \approx 1-\frac {1}{2}x^{2}\) give correct results to 3 decimal places.
A small code to verify:

Problem: First develop the function \(\sqrt {x}\) in a series of powers of \(\left (x-1\right ) \) and then use it to approximate \(\sqrt {0.99999\ 99995}\) to 10 decimal places.
Solution:
\[ \sqrt {x}=a_{0}+a_{1}\left (x-x_{0}\right ) +a_{2}\left (x-x_{0}\right ) ^{2}+a_{3}\left (x-x_{0}\right ) ^{3}+\cdots +a_{n}\left (x-x_{0}\right ) ^{n}+\cdots \]
Expand at \(x_{0}=1\)
\[ \sqrt {x}=a_{0}+a_{1}\left (x-1\right ) +a_{2}\left (x-1\right ) ^{2}+a_{3}\left (x-1\right ) ^{3}+\cdots +a_{n}\left (x-1\right ) ^{n}+\cdots \]
at \(x=1\rightarrow a_{0}=1\), differentiating the above we obtain
\[ \frac {1}{2\sqrt {x}}=a_{1}+2a_{2}\left (x-1\right ) +3a_{3}\left (x-1\right ) ^{2}+\cdots +na_{n}\left (x-1\right ) ^{n-1}+\cdots \]
at \(x=1\rightarrow a_{1}=\frac {1}{2}\), differentiate the above we obtain
\[ \frac {-1}{4\relax (x) ^{3/2}}=2a_{2}+\left (3\times 2\right ) a_{3}\left (x-1\right ) +\cdots +n\left (n-1\right ) a_{n}\left (x-1\right ) ^{n-2}+\cdots \]
at \(x=1\rightarrow a_{2}=-\frac {1}{4\times 2}=-\frac {1}{8}\), differentiate the above we obtain
\[ \frac {3}{8\relax (x) ^{5/2}}=\left (3\times 2\right ) a_{3}+\cdots +n\left (n-1\right ) \left (n-2\right ) a_{n}\left (x-1\right ) ^{n-3}+\cdots \]
at \(x=1\rightarrow a_{3}=\frac {3}{8\left (3\times 2\right ) }=\frac {1}{16}\) differentiating the above gives
\[ -\frac {15}{16\relax (x) ^{7/2}}=\left (4\times 3\times 2\right ) a_{4}+\cdots +n\left (n-1\right ) \left (n-2\right ) \left (n-3\right ) a_{n}\left (x-1\right ) ^{n-4}+\cdots \]
at \(x=1\rightarrow a_{4}=-\frac {15}{16\left (4\times 3\times 2\right ) }=-\frac {5}{128}\)
Hence the series is
\[ \sqrt {x}=1+\frac {1}{2}\left (x-1\right ) -\frac {1}{8}\left (x-1\right ) ^{2}+\frac {1}{16}\left (x-1\right ) ^{3}-\frac {5}{128}\left (x-1\right ) ^{4}+\cdots \]
Note: For convergence we require \(\left \vert x\right \vert \leq 1\)
We want accuracy to 10 decimal places. Since
\[ \sqrt {0.99999\ 99995}=0.9999\ 999974 \]
Then the series, using 2 terms gives
\[ \sqrt {0.99999\ 99995}\approx \left (1+\frac {1}{2}\left (x-1\right ) \right ) _{x=0.9999999995}=1+\frac {1}{2}\left (0.9999999995-1\right ) =0.9999\ 999975 \]
hence 2 terms are only needed. hence \(n=1\)
Problem: For the pair \(\left (x_{n},\alpha _{n}\right ) \), is it true that \(x_{n}=O\left (\alpha _{n}\right ) \) as \(n\rightarrow \infty ?\)
b) \(x_{n}=5n^{2}+9n^{3}+1,\alpha _{n}=1\)
e) \(x_{n}=\sqrt {n+3},\alpha _{n}=\frac {1}{n}\)
Solution:
b) Assume that \(5n^{2}+9n^{3}+1\leq C\left (\alpha _{n}\right ) \) hence \(5n^{2}+9n^{3}+1\leq C\), but since \(n>1\) and keeps increasing, then no matter how large a \(C\) we select, \(5n^{2}+9n^{3}\) will eventually become larger than any constant \(C\) we choose when \(n>N\,\ \) for sufficiently large \(N\).
Hence there is no such \(C\), hence the answer is NOT TRUE.
e) we see that \(lim_{n\rightarrow \infty }x_{n}=\infty \), however \(\lim _{n\rightarrow \infty }\frac {1}{n}=0\), hence it is not possible to find \(C\) s.t. \(\sqrt {n+3}\leq C\frac {1}{n}\) for any \(N\). Hence the answer is NOT TRUE.
Problem: Choose the correct assertion (in each, \(n\rightarrow \infty )\)
b) \(\frac {n+1}{\sqrt {n}}=o\relax (1) \)
c)\(\frac {1}{\ln n}=O\left (\frac {1}{n}\right ) \)
Solution:
b) \(x_{n}=\frac {n+1}{\sqrt {n}},\alpha _{n}=1\).
\begin {align*} \lim _{n\rightarrow \infty }\left (\frac {x_{n}}{\alpha _{n}}\right ) & =\lim _{n\rightarrow \infty }\left (\frac {n+1}{\sqrt {n}}\right ) \\ & =\lim _{n\rightarrow \infty }\left (\frac {n+1}{\sqrt {n}}\right ) \\ & =\lim _{n\rightarrow \infty }\left (\frac {n}{\sqrt {n}}\right ) +\lim _{n\rightarrow \infty }\left (\frac {1}{\sqrt {n}}\right ) \\ & =\lim _{n\rightarrow \infty }\left (\sqrt {n}\right ) +0\\ & \neq 0 \end {align*}
Since the limit as \(n\rightarrow \infty \) is not zero, hence the assertion is FALSE
c)\(x_{n}=\frac {1}{\ln n},\alpha _{n}=\frac {1}{n}\). Since \(\ln n\) grows less rapidly than \(n\,\ \)then \(\frac {1}{\ln n}\)grows more rapidly than \(\frac {1}{n}\), Hence it is not possible to find some constant \(C\) s.t. \(\frac {1}{\ln n}\leq C\frac {1}{n}\) , hence assertion is FALSE
Problem: Show that these assertions are not true:
a) \(e^{x}-1=O\left (x^{2}\right ) \) as \(x\rightarrow 0\)
b) \(x^{-2}=O\left (\cot x\right ) \) as \(x\rightarrow 0\)
c) \(\cot x=o\left (x^{-1}\right ) \) as \(x\rightarrow 0\)
Answer:
a) We need to \begin {align*} x_{n} & =e^{x}-1\\ & =\left (1+x+\frac {x^{2}}{2!}+\frac {x^{3}}{3!}+\cdots \right ) -1\\ & =x+\frac {x^{2}}{2!}+\frac {x^{3}}{3!}+\cdots \end {align*}
and \(\alpha _{n}=x^{2}\)
As \(x\rightarrow 0\,\ \)the term \(x\) will become larger than \(x^{2}\), hence near \(x=0\), \(x_{n}>\alpha _{n}\) since near \(x=0\) \(x+\frac {x^{2}}{2!}+\frac {x^{3}}{3!}+\cdots >x^{2}\)
Therefore it is not possible to find a constant \(C\) such that \(x_{n}\leq C\alpha _{n}\) near \(x=0\) since for any constant \(C\) we select, no matter how small, we can find \(x\) closer to zero such that \(x_{n}>C\alpha _{n}\), Hence assertion is not true.
b) The power series for \(\cot \relax (x) \) is (Using CAS:).
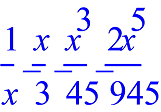
Here we have \(x_{n}=x^{-2}\) and \(\alpha _{n}=\frac {1}{x}-\frac {x}{3}-\frac {x^{3}}{45}-\cdots \)
As \(x\rightarrow 0\), \(\ \)then \(\alpha _{n}\rightarrow \frac {1}{x}\)
But \(\frac {1}{x}\) will grow less rapidly than \(\frac {1}{x^{2}}\)would as \(x\rightarrow 0\), hence it is not possible to find a constant \(C\) such that \(x_{n}\leq C\alpha _{n}\) near \(x=0\) since for any constant \(C\) we select, no matter how small, can find \(x\) closer to zero such that \(x_{n}>C\alpha _{n}\), Hence assertion is not true.
c) \(x_{n}=\cot \relax (x) =\frac {1}{x}-\frac {x}{3}-\frac {x^{3}}{45}-\cdots ,\alpha _{n}=\frac {1}{x}\), hence
\begin {align*} \lim _{x\rightarrow 0}\frac {x_{n}}{\alpha _{n}} & =\lim _{x\rightarrow 0}\frac {\frac {1}{x}-\frac {x}{3}-\frac {x^{3}}{45}-\cdots }{\frac {1}{x}}\\ & =\lim _{x\rightarrow 0}\frac {\frac {1}{x}\left (1-\frac {x^{2}}{3}-\frac {x^{4}}{45}-\cdots \right ) }{\frac {1}{x}}\\ & =\lim _{x\rightarrow 0}\left (1-\frac {x^{2}}{3}-\frac {x^{4}}{45}-\cdots \right ) \\ & =1 \end {align*}
Since the limit does not go to zero, hence the assertion is not true.
Problem: Prove that \(x_{n}=x+o\relax (1) \) iff \(\lim _{n\rightarrow \infty }x_{n}=x\)
Solution:
Let \(X_{n}=x_{n}-x,\alpha _{n}=1\)
Forward direction proof:
\begin {align*} \lim _{n\rightarrow \infty }X_{n} & =\lim _{n\rightarrow \infty }\left ( x_{n}-x\right ) \\ & =\left (\lim _{n\rightarrow \infty }x_{n}\right ) -\left (\lim _{n\rightarrow \infty }x\right ) \\ & =\left (\lim _{n\rightarrow \infty }x_{n}\right ) -x \end {align*}
If \(\lim _{n\rightarrow \infty }x_{n}=x\), then the above become \(x-x=0\)
Hence \(\lim _{n\rightarrow \infty }\frac {X_{n}}{\alpha _{n}}=\frac {0}{1}=0\), hence \(X_{n}=o\relax (1) \) or \(x_{n}-x=o\relax (1) \) or \(x_{n}=x+o\relax (1) \)
Now proof in the reverse direction. Assume that \(\lim _{n\rightarrow \infty }x_{n}\neq x\), we need to show that this implies \(x_{n}\neq x+o\left ( 1\right ) \)
If \(\lim _{n\rightarrow \infty }x_{n}\neq x\), then we can say that \(\lim _{n\rightarrow \infty }x_{n}=\beta \), where \(\beta \neq x\), hence \(\lim _{n\rightarrow \infty }X_{n}=\beta -x\)
Hence \begin {align*} \lim _{n\rightarrow \infty }\frac {X_{n}}{\alpha _{n}} & =\lim _{n\rightarrow \infty }\frac {\beta -x}{\alpha _{n}}\\ & =\frac {\beta -x}{1}\\ & =\beta -x \end {align*}
But since \(\beta \neq x\), then this limit does not go to zero. Hence \(x_{n}\neq x+o\relax (1) \). This complete the proof.
Problem: Prove: If \(\alpha _{n}\rightarrow 0\), \(x_{n}=O\left ( \alpha _{n}\right ) \), and \(y_{n}=O\left (\alpha _{n}\right ) \) then \(x_{n}y_{n}=o\left (\alpha _{n}\right ) \)
Answer: Since \(x_{n}=O\left (\alpha _{n}\right ) \) then \(x_{n}\leq C_{1}\left (\alpha _{n}\right ) \), and since \(y_{n}=O\left (\alpha _{n}\right ) \) then \(y_{n}\leq C_{2}\left (\alpha _{n}\right ) ,\) where \(C_{1},C_{2}\) are positive constants.
Hence \begin {align*} x_{n}y_{n} & \leq C_{1}C_{2}\left (\alpha _{n}\right ) \\ & \leq C\left (\alpha _{n}\right ) \end {align*}
Where \(C=C_{1}C_{2}\)
But \(x_{n}y_{n}\leq C\left (\alpha _{n}\right ) \) means that \(x_{n}y_{n}\) is bounded above by \(\alpha _{n}\).
But we are told next that \(\lim _{n\rightarrow \infty }\alpha _{n}=0\), hence this means that the sequence \(x_{n}y_{n}\) will reach zero before the sequence \(\alpha _{n}\). But this is the same as saying that \(x_{n}y_{n}=o\left ( \alpha _{n}\right ) \)
Problem: Prove that if \(L_{1}\) and \(L_{2}\) are linear combinations of powers of \(E\) and if \(L_{1}x=0\), then \(L_{1}L_{2}x=0\)
Answer: Let \(L_{1}=a_{1}E^{n_{1}}+a_{2}E^{n_{2}}+\cdots \) and \(L_{2}=b_{1}E^{m_{1}}+b_{2}E^{m_{2}}+\cdots \)
Then \begin {align*} L_{1}L_{2}x & =\left (a_{1}E^{n_{1}}+a_{2}E^{n_{2}}+\cdots \right ) \left ( b_{1}E^{m_{1}}+b_{2}E^{m_{2}}+\cdots \right ) x\\ & =\left (a_{1}E^{n_{1}}+a_{2}E^{n_{2}}+\cdots \right ) \left (b_{1}E^{m_{1}}x+b_{2}E^{m_{2}}x+\cdots \right ) \\ & \\ & =\left (a_{1}E^{n_{1}}\left (b_{1}E^{m_{1}}x\right ) +a_{2}E^{n_{2}}\left (b_{1}E^{m_{1}}x\right ) +\cdots \right ) \\ & +\left (a_{1}E^{n_{1}}\left (b_{2}E^{m_{2}}x\right ) +a_{2}E^{n_{2}}\left (b_{2}E^{m_{2}}x\right ) +\cdots \right ) \\ & +\cdots \\ & =\left (b_{1}a_{1}E^{n_{1}}\left (E^{m_{1}}x\right ) +b_{1}a_{2}E^{n_{2}}\left (E^{m_{1}}x\right ) +\cdots \right ) \\ & +\left (b_{2}a_{1}E^{n_{1}}\left (E^{m_{2}}x\right ) +b_{2}a_{2}E^{n_{2}}\left (E^{m_{2}}x\right ) +\cdots \right ) \\ & +\cdots \\ & =\left (b_{1}a_{1}E^{m_{1}}\left (E^{n_{1}}x\right ) +b_{1}a_{2}E^{m_{1}}\left (E^{n_{2}}x\right ) +\cdots \right ) \\ & +\left (b_{2}a_{1}E^{m_{2}}\left (E^{n_{1}}x\right ) +b_{2}a_{2}E^{m_{2}}\left (E^{n_{2}}x\right ) +\cdots \right ) \\ & +\cdots \\ & =\left (b_{1}E^{m_{1}}+b_{2}E^{m_{2}}+\cdots \right ) \left (a_{1}E^{n_{1}}x+a_{2}E^{n_{2}}x+\cdots \right ) \\ & =L_{2}L_{1}x\\ & =L_{2}\relax (0) \\ & =0 \end {align*}
Problem: Give bases consisting of real sequences for each solution space.
a) \(\left (4E^{0}-3E^{2}+E^{3}\right ) x=0\)
b) \(\left (3E^{0}-2E+E^{2}\right ) x=0\)
c) \(\left (2E^{6}-9E^{5}+12E^{4}-4E^{3}\right ) x=0\)
d) \(\left (\pi E^{2}-\sqrt {2}E+E^{0}\log 2\right ) x=0\)
Solution:
a) Characteristic equation is \(\lambda ^{3}-3\lambda ^{2}+4=0\), or \(\left ( \lambda +1\right ) \left (\lambda -2\right ) ^{2}=0\), hence the roots are \(\lambda =-1\), and \(\lambda =2\) or multiplicity 2.
i.e. \(\lambda _{1}=-1,\lambda _{2}=2,\lambda _{3}=2\)
Hence first solution \(x_{1}\relax (n) \ \)associated with \(\lambda _{1}=-1\ \)is \(x_{1}\relax (n) =\lambda _{1}^{n}=-1^{n}\)
the second solution \(x_{2}\relax (n) \ \)associated with \(\lambda _{2}=-2\ \)is \(x_{2}\relax (n) =\lambda _{2}^{n}=2^{n}\)
the third solution \(x_{3}\relax (n) \ \)associated with \(\lambda _{3}=-2\ \)is \(x_{3}\relax (n) =\frac {dx_{2}\relax (n) }{d\lambda }=n\lambda _{2}^{n-1}=n2^{n-1}\)
Hence now we can write some terms of the above 3 basis solutions are follows
\begin {align*} x_{1}\relax (n) & =\left [ \lambda _{1}^{1},\lambda _{1}^{2},\lambda _{1}^{3},\cdots \right ] \\ & =\left [ -1,-1^{2},-1^{3},\cdots \right ] \\ & =\left [ -1,1,-1,1,\cdots \right ] \\ & \\ x_{2}\relax (n) & =\left [ \lambda _{2}^{1},\lambda _{2}^{2},\lambda _{2}^{3},\cdots \right ] \\ & =\left [ 2^{1},2^{2},2^{3},\cdots \right ] \\ & =\left [ 2,4,8,16,32,\cdots \right ] \\ & \\ x_{3}\relax (n) & =\left [ \lambda _{2}^{0},2\lambda _{2}^{1},3\lambda _{2}^{2},4\lambda _{2}^{3},\cdots \right ] \\ & =\left [ \left (2^{0}\right ) ,2\left (2^{1}\right ) ,3\left ( 2^{2}\right ) ,4\left (2^{3}\right ) ,5\left (2^{4}\right ) ,\cdots \right ] \\ & =\left [ 1,4,12,32,80,\cdots \right ] \end {align*}
Hence the basis are
\begin {align*} & \left [ -1,1,-1,1,\cdots \right ] \\ & \left [ 2,4,8,16,32,\cdots \right ] \\ & \left [ 1,4,12,32,80,\cdots \right ] \end {align*}
b)\(\left (3E^{0}-2E+E^{2}\right ) x=0\)
Characteristic equation is \(\lambda ^{2}-2\lambda +3=0\), The roots are \begin {align*} \lambda _{1} & =1+\sqrt {2}i\\ \lambda _{2} & =1-\sqrt {2}i \end {align*}
Hence first solution \(x_{1}\relax (n) \ \)associated with \(\lambda _{1}=1+\sqrt {2}i\ \)is \(x_{1}\relax (n) =\lambda _{1}^{n}=\left ( 1+\sqrt {2}i\right ) ^{n}\)
the second solution \(x_{2}\relax (n) \)associated with \(\lambda _{2}=1-\sqrt {2}i\ \)is \(x_{2}\relax (n) =\lambda _{2}^{n}=\left ( 1-\sqrt {2}i\right ) ^{n}\)
Hence \begin {align*} x_{1}\relax (n) & =\lambda _{1}^{n}\\ & =\left [ \left (1+\sqrt {2}i\right ) ^{1},\left (1+\sqrt {2}i\right ) ^{2},\left (1+\sqrt {2}i\right ) ^{3},\cdots \right ] \\ & =\left [ \left (1+\sqrt {2}i\right ) ,\left (-1+2i\sqrt {2}\right ) ,\left (-5+i\sqrt {2}\right ) ,\left (-7-4i\sqrt {2}\right ) ,\cdots \right ] \\ & \\ x_{2}\relax (n) & =\left [ \left (1-\sqrt {2}i\right ) ^{1},\left ( 1-\sqrt {2}i\right ) ^{2},\left (1-\sqrt {2}i\right ) ^{3},\cdots \right ] \\ & =\left [ \left (1-\sqrt {2}i\right ) ,\left (-1-2i\sqrt {2}\right ) ,\left (-5-i\sqrt {2}\right ) ,\left (-7+4i\sqrt {2}\right ) \cdots \right ] \end {align*}
Notice that the 2 basis are conjugate to each others in each term in the sequence.
c)\(\left (2E^{6}-9E^{5}+12E^{4}-4E^{3}\right ) x=0\)
Characteristic equation is \(2\lambda ^{6}-9\lambda ^{5}+12\lambda ^{4}-4\lambda ^{3}=0\)
Factoring we obtain \(\lambda \)\[ ^{3}\left (2\lambda -1\right ) \left (\lambda -2\right ) ^{2}=0 \] hence the solutions are
\(\lambda =0\) with multiplicity 3, \(\lambda =\frac {1}{2},\lambda =2\) with multiplicity 2.
Hence Solutions associated with \(\lambda =0\) are
\(x_{1}\relax (n) =\lambda ^{n},x_{2}\relax (n) =n\lambda ^{n-1},x_{3}\relax (n) =n\left (n-1\right ) \lambda ^{n-2}\)
Hence \(x_{1}\relax (n) =\left [ 0,0,0,\cdots \right ] \), and \(x_{2}\) and \(x_{3}\) are also the null sequence.
Solution associated with \(\lambda =\frac {1}{2}\) is \(x_{4}\left ( n\right ) =\lambda ^{n}=\left (\frac {1}{2}\right ) ^{n}=\left [ \frac {1}{2},\frac {1}{4},\frac {1}{8},\frac {1}{16},\cdots \right ] \)
Solutions associated with \(\lambda =2\) are \(x_{5}\relax (n) =\lambda ^{n}=2^{n}=\left [ 2,4,8,16,\cdots \right ] \)
and \(x_{6}\relax (n) =\frac {dx_{5}}{d\lambda }=n\lambda ^{n-1}=n2^{n-1}=\left [ 1,2\relax (2) ,3\left (2^{2}\right ) ,4\left ( 2^{3}\right ) ,\cdots \right ] =\left [ 1,4,12,32,\cdots \right ] \)
Hence the basis are
\begin {align*} & \left [ 0,0,0,\cdots \right ] \\ & \left [ \frac {1}{2},\frac {1}{4},\frac {1}{8},\frac {1}{16},\cdots \right ] \\ & \left [ 2,4,8,16,\cdots \right ] \\ & \left [ 1,4,12,32,\cdots \right ] \end {align*}
d)\(\left (\pi E^{2}-\sqrt {2}E+E^{0}\log 2\right ) x\)
Characteristic equation is \begin {align*} \pi \lambda ^{2}-\sqrt {2}\lambda +\log 2 & =0\\ \lambda ^{2}-\frac {\sqrt {2}}{\pi }\lambda +\frac {\log 2}{\pi } & =0\\ \lambda ^{2}-0.450\,16\ \lambda +0.220\,64 & =0 \end {align*}
\begin {align*} \lambda & =\frac {-b\pm \sqrt {b^{2}-4ac}}{2a}=\frac {0.450\,16\pm \sqrt {0.450\,16^{2}-4\times 0.220\,64}}{2}\\ & =\allowbreak \frac {0.450\,16\pm \sqrt {-0.679\,92}}{2}\\ & =\frac {0.450\,16\pm i0.824\,57}{2} \end {align*}
Hence \(\lambda _{1}=0.225079+i0.41228\) and \(\lambda _{2}=0.225079-i0.41228\)
Hence \begin {align*} x_{1} & =\lambda _{1}^{n}\\ & =\left (0.225079+i0.41228\right ) ^{n} \end {align*}
and \begin {align*} x_{2} & =\lambda _{2}^{n}\\ & =\left (0.225079-i0.41228\right ) ^{n} \end {align*}
Problem: Prove that if P is a polynomial with real coefficients and if \(z\equiv \left [ z_{1},z_{2},z_{3},\cdots \right ] \) is a complex solution of \(p\relax (E) z=0,\) then the conjugate of \(z\), the real part of \(z\) and the imaginary part of \(z\) are also solutions.
Solution:
\[ P\relax (E) z=0 \]
Take conjugate of both sides
\begin {align*} \overline {P\relax (E) \ z} & =\overline {0}\\ \overline {P\relax (E) }\ \overline {z} & =0 \end {align*}
But \[ P\relax (E) =a_{0}E^{0}+a_{1}E^{1}+a_{2}E^{2}+\cdots \]
and all the \(a^{\prime }s\) are real, hence \(\overline {P\relax (E) }=P\relax (E) \), then \begin {equation} P\relax (E) \bar {z}=0 \tag {1} \end {equation}
Now take the real part of \(P\relax (E) z=0\,\) we get
\begin {align*} \operatorname {Re}\left (P\relax (E) z\right ) & =\operatorname {Re}\relax (0) \\ \operatorname {Re}\left (P\relax (E) \right ) \operatorname {Re}\left ( z\right ) & =0 \end {align*}
But \[ \operatorname {Re}\left (P\relax (E) \right ) =P\relax (E) \]
Hence \begin {equation} P\relax (E) \operatorname {Re}\relax (z) =0 \tag {2} \end {equation}
For the last part, let \[ z=\operatorname {Re}\relax (z) +i\ \operatorname {Im}\relax (z) \]
Then \(P\relax (E) z=0\) can be written as
\begin {align*} P\relax (E) \left \{ \operatorname {Re}\relax (z) +i\ \operatorname {Im}\relax (z) \right \} & =0\\ P\relax (E) \operatorname {Re}\relax (z) +i\ P\relax (E) \operatorname {Im}\relax (z) & =0 \end {align*}
But from (2) we see that \(P\relax (E) \operatorname {Re}\left ( z\right ) =0\,,\) hence the above becomes
\[ i\ P\relax (E) \operatorname {Im}\relax (z) =0 \]
Hence
\[ P\relax (E) \operatorname {Im}\relax (z) =0 \]
Problem: Determine if the difference equation \(x_{n}=x_{n-1}+x_{n-2}\)
Solution: Using the shift operator, we write \(E^{2}x_{n-2}=Ex_{n-1}+E^{0}x_{n-2}\)
Hence
\begin {align*} E^{2}x_{n-2}-Ex_{n-2}-E^{0}x_{n-2} & =0\\ \left (E^{2}-E-1\right ) x_{n-2} & =0 \end {align*}
Hence the roots of the characteristic polynomial \(p\relax (E) x=0\) are \(\lambda ^{2}-\lambda -1=0\,\ \) or \(\lambda =\frac {-b\pm \sqrt {b^{2}-4ac}}{2a}\), hence \(\lambda =\frac {1\pm \sqrt {1+4}}{2}=\frac {1\pm \sqrt {5}}{2}\)
Hence \(\left \vert \lambda _{1}\right \vert =\left \vert \frac {1+\sqrt {5}}{2}\right \vert =\) \(1.\,\allowbreak 618\) and \(\left \vert \lambda _{2}\right \vert =\left \vert \frac {1-\sqrt {5}}{2}\right \vert \) \(=0.618\,03\)
Since \(\lambda _{1}\geq 1\), then NOT STABLE difference equation.