5.48 Fourier series in maple

I wrote this to generate FS in Maple for some HW I was doing. I think this was for Math 121A at UC Berkeley in 2003

restart; 
f:=x->piecewise(-Pi<x and x<Pi/2,-1, 
                Pi/2<x and x<1,0,1); 
 
assume(n,integer); 
 
nmaFourier2:=proc(f,freq,from_,to_,maxN) 
       local n::integer,denomC,denomS,a,b; 
       denomC:=( to_ - from_ ) / 2; 
       denomS:=( to_ - from_ ) / 2; 
 
       a:=proc(n) 
         int(f(x)*cos(n*freq*x),x=from_..to_) /denomC; 
       end proc; 
 
       b:=proc(n) 
         int(f(x)*sin(n*freq*x),x=from_..to_) / denomS; 
       end proc; 
 
       evalf(denomC); 
 
       1/2*a(0) + sum( a(n) * cos(n*freq*x) ,n=1..maxN) 
                + sum( b(n) * sin(n*freq*x) ,n=1..maxN) 
end proc; 
 
r:=[seq(nmaFourier2(f,1,-Pi,Pi,nIter),nIter=1..10)]; 
plot(r,x=-Pi..Pi);
 

To animate do

g:=n->plot(nmaFourier2(f,1,-Pi,Pi,n),x=-2*Pi..2*Pi); 
plots:-animate(g,[n],n=1..40);
 

Here is the animation from the Maple notebook:

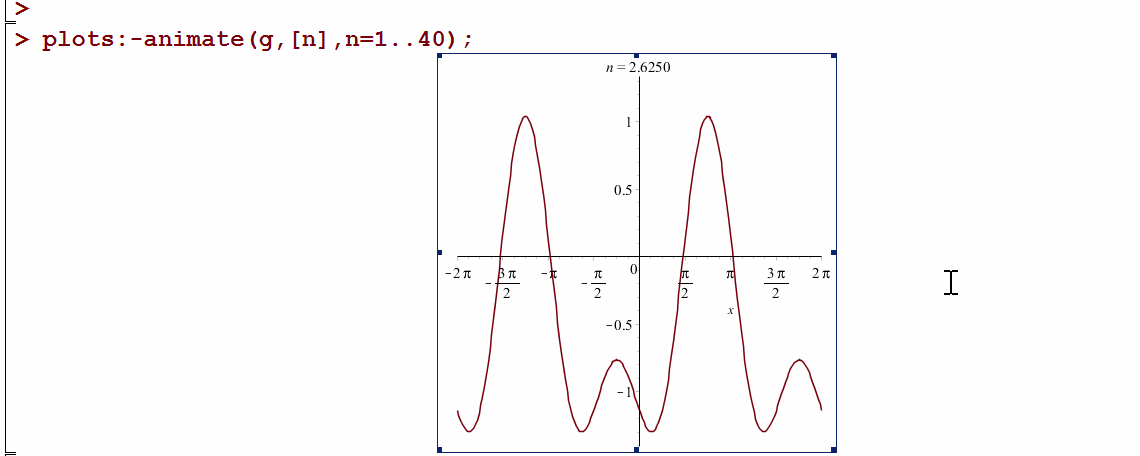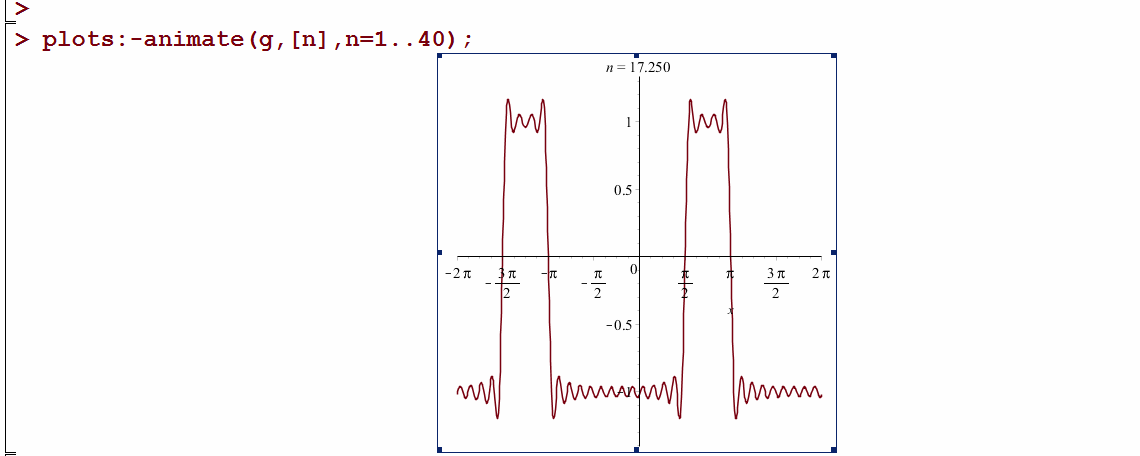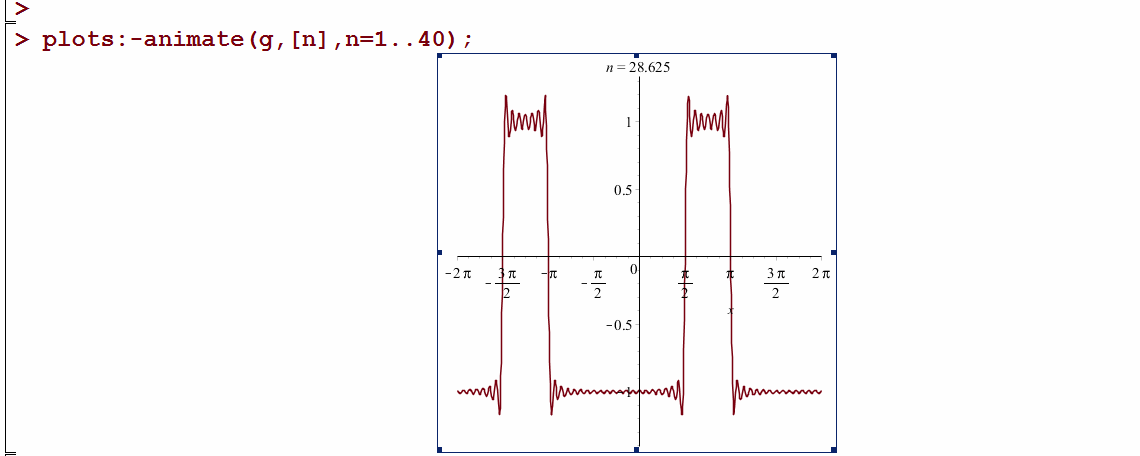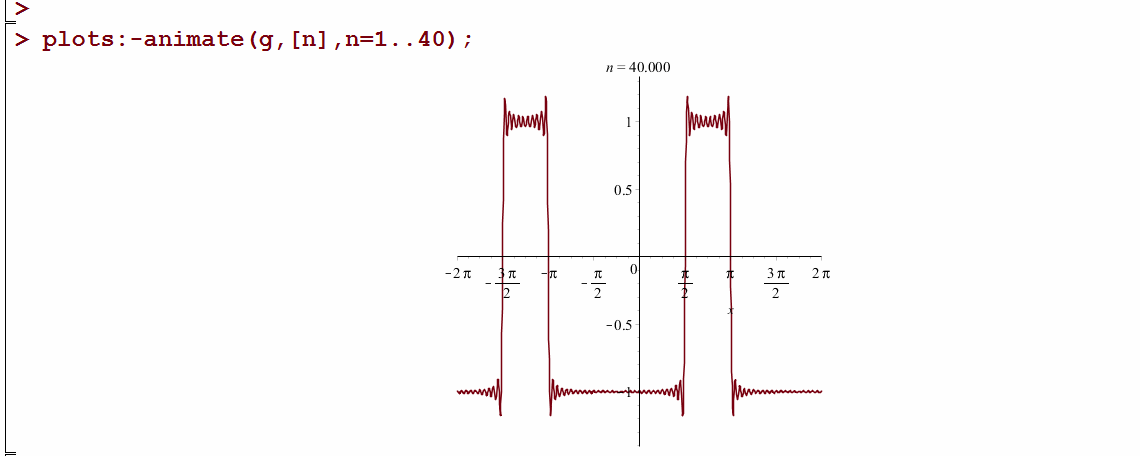
Another version

restart; 
f:=x->piecewise(-Pi<x and x<Pi/2,-1, 
                Pi/2<x and x<1,0,1); 
 
assume(n,integer); 
nmaFourier2:=proc(f,freq,from_,to_,maxN::integer) 
       local n::integer,denomC,denomS,a,b; 
 
       denomC:=( to_ - from_ ) / 2; 
       denomS:=( to_ - from_ ) / 2; 
 
       a:=proc(n) 
         int(f(x)*cos(n*freq*x),x=from_..to_) /denomC; 
       end proc; 
 
       b:=proc(n) 
         int(f(x)*sin(n*freq*x),x=from_..to_) / denomS; 
       end proc; 
 
       1/2*a(0) + sum( a(n) * cos(n*freq*x) ,n=1..maxN) 
                + sum( b(n) * sin(n*freq*x) ,n=1..maxN) 
end proc; 
 
plots[setoptions](title=` `, axesfont=[SYMBOL,8] ,font=[COURIER,1], 
   xtickmarks=[seq(evalf(k*Pi/2)=sprintf("%a %s", k/2 ,"pi" ),k= -3..3)], 
   ytickmarks=[-1.0="-1",-0.5="",0.0="0",0.5="",1.0="1"]); 
 
B:=array(1..3,1..3); 
k:=0; 
for i from 1 to 3 do 
    for j from 1 to 3 do 
       k:=k+1; 
       B[i,j]:=plot({f(x),nmaFourier2(f,1,-Pi,Pi,k)},x=-Pi..Pi,size=[200,100]); 
    end do; 
end do; 
 
plots:-display( B);