Comparing total error against truncation error at each grid point resulting from the numerical solution of u''(x)=exp(x) using finite difference discretization
Nasser M. Abbasi, 10/25/2010
Introduction
The differential equation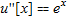 
with Dirichlet boundary conditions u[0]=0,u[1]=0 is solved numerically by approximating u''[x] by 
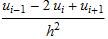where h is the spacing between grid points. The truncation error τ at each 
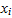is given by 
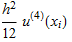while the total error e at the same point is given by 
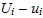where 
is the numerical solution found at that point and 
is the exact solution u(x) evaluated at the same point.
A small program is written to show the distribution of e and τ along the length of the domain [0,1] as h is made smaller and smaller.
This was run for few iterations, where h was divided by half each time, the system was solved for U and the result is shown in a series of plots.
Results
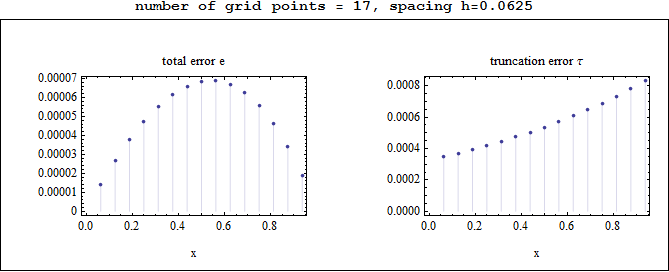
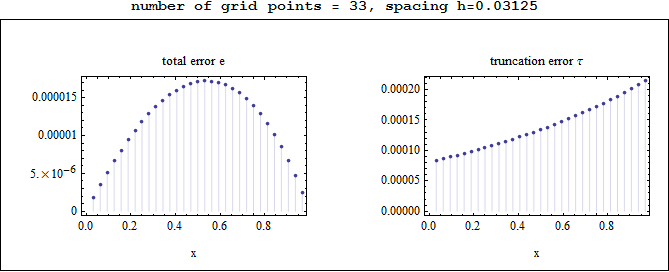
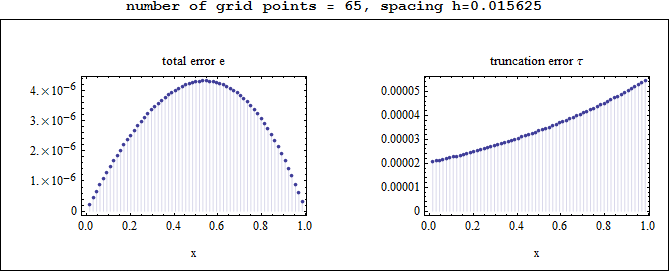
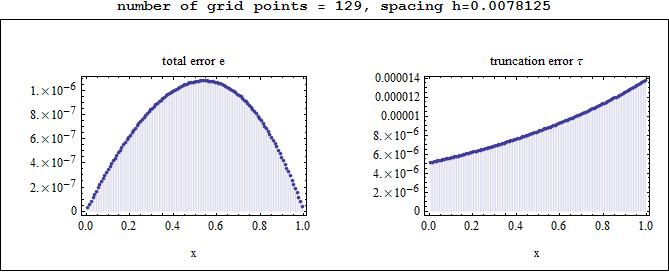
Observations on the above plots
The total error e was largest in the middle of the grid, and smallest at the edges, while the truncation error was smallest at the left edge and largest at the right edge.
Comparing e to τ on each grid point is useful to understand the distribution of errors along the domain, but for verification that the numerical solution converges to the exact solution as h becomes smaller, the grid norm of e is the one examined to verify that it is less than or equal to the grid norm of τ.
Therefore, the following plots are generated which shows how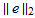 
compares to 
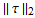as h becomes smaller. These norms are grid norms and not the standard norms.
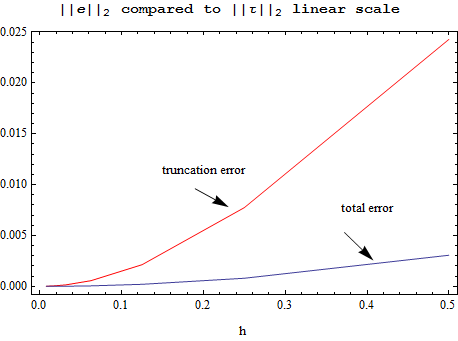
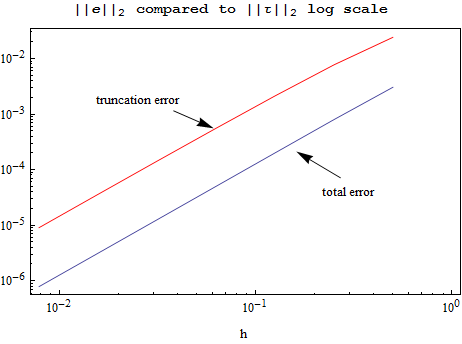
Observations on the above plots
The total error has smaller grid norm. This shows convergence, since this implies that ||e||≤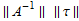
, therefore showing that 
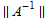=O(1) which is the condition for convergence. The above results confirms this for this problem.
