Equivalence of finite element solution using Rayleigh Ritz method and Galerkin method for finding axial deformation of a simple cantilever beam, and on how to determine if the approximate solution found is an exact solution.
by Nasser M. Abbasi
Student, Engineering Mechanics dept.
University of Wisconsin, Madison
oct 16, 2009
Abstract
Using a simple problem, it is shown that, using a global trial function, the Rayleigh Ritz variational method and the Galerkin method give the same solution. These solutions are compared to the exact solution. It is found that one can determine that the exact solution was reached by increasing the order of the trial function polynomial until the solution returned by Rayleigh Ritz or Galerkin method no longer changes.
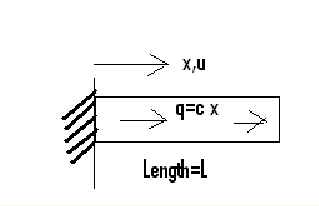
The problem
A cantilever beam is loaded with traction load of q = c x (for some constant c). It is fixed on the left side. We need to find axial deformation u (x)
Solving using variational Ritz method
Set up the potential energy 
and Minimize it
 |
where u (x) is the trial function . The trial function needs to satisfy only the essential conditions, which in this problem is given as u (0) = 0, so we start by assuming a trial function u(x).
 |
Since u(0)=0 , we find that 
hence
 |
This trial function has 2 degrees of freedom they are called the generalized degrees of freedom. The trial function could have been selected to have only one degree of freedom i.e. 
and this would also have worked but 2 degrees of freedom will give more accurate solution.
Start by defining the trial function
Make the trial function satisfy essential boundary condition
Set up the potential energy functional
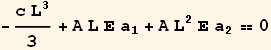
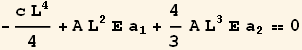
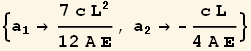
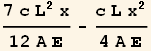
Solving the problem using Galerkin method
In this method, we start with the differential equation itself and integrate it with a test function we call g (x). The differential equation for axial deformation with traction load q(x) is 
, hence our starting point is to solve the integral equation
We start by assuming a trial function 
. Now due to u(0)=0 we find that 
, hence 
Next, we do integration by parts the above integral and obtain
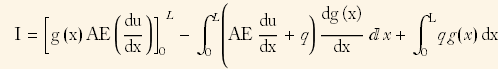
But
and now since a test function must also satisfy the essential conditions, hence g(0)=0 and also the trial function satisfies the natural boundary conditions at x=L which is that there is no load at that point, hence this means A E (du/dx) = 0 since this is the load at the end. Hence the integral becomes
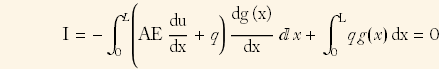
We now pick the test function g(x). In Galerkin method, 
hence 
and 
so now we set up the 2 equations and solve for 
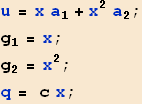
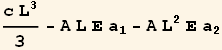
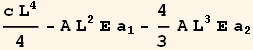
Now solve for 
and 
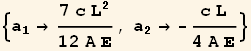
Substitute the above into the original u(x)
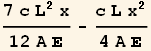
We see that this solution is the same as the one found from the Ritz method
Exact solution for the problem
The ODE is
|
With the essential conditions u(0)=0 and with natural boundary condition A E u'[x]=0 at x=L. Find exact solution:
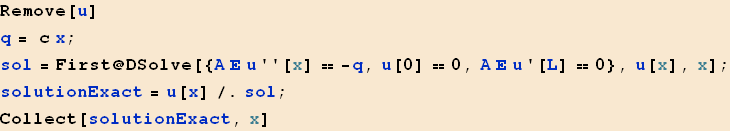
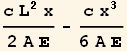
Compare the above solution to the one found above, we see that the approximate solution is
while the exact solution is
here is a plot of both solutions. Assume A = 1, c = 1, E = 1 and L = 1, we obtain
How can we improve the FEM solution, can we make it match the exact solution?
Make the trial function a polynomial of higher order. Try
and repeat Ritz method. Instead of making the same steps as above, let us write a function which accepts a trial function u(x) and returns back the solution. Find define the function
Now we can call the above function for the trial function shown above to dtermine the values of the 
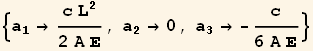
We see now that the FEM solution is the same as the exact solution. We can confirm this by taking the difference between them
What happens if we add more terms to the trial functions? We should expect that the solution would not change. This is confirmed by the following table generated using the above function
 |
 |
 |
 |
 |
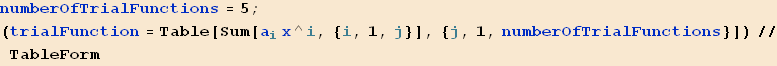
Now find the solution using each of the above trial functions using Ritz method
| TrialFunction | Solution |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
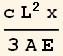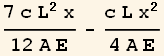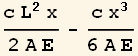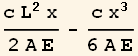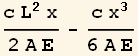We see from the above that as more terms added to the trial function, after the cubic polynomial, the solution no longer changes. This implies, at least in this example, that the exact solution was reached. (Need to find a formal proof of this).
