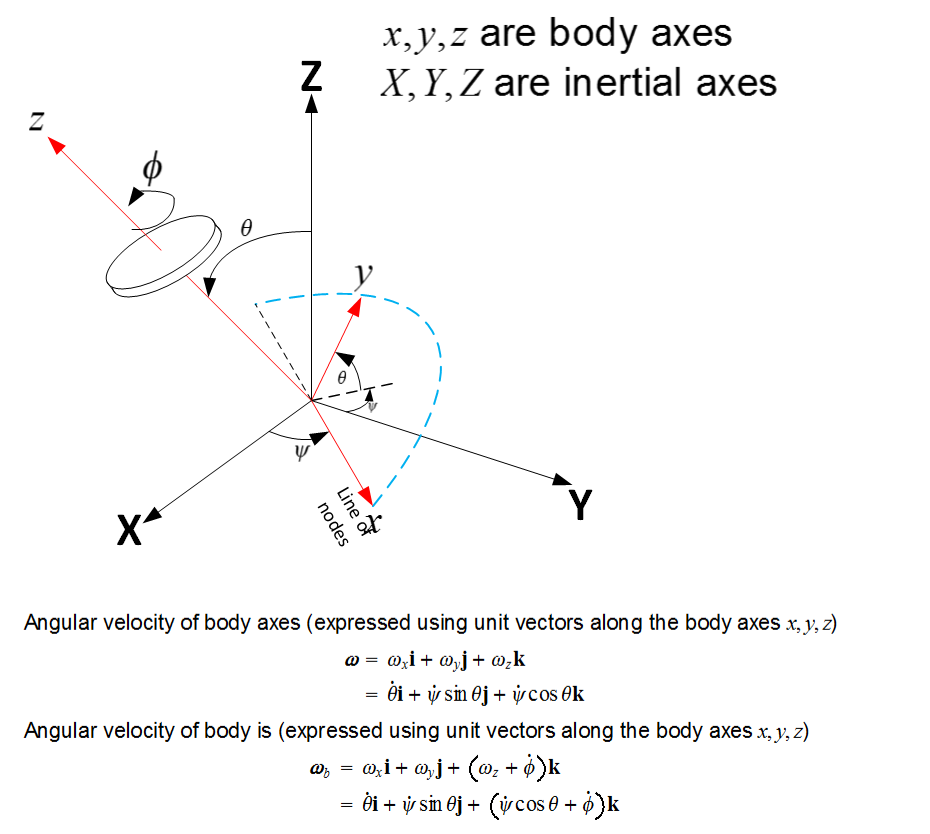
Let be the body axes. In this case, the body spins around one of its body axes (the z-axis). This is
different from other cases looked at before where the body axes and the body all move with same angular
velocities.
Let be the inertial axes. Angular velocity of body axes (expressed using unit vectors along the
body axes
) is
The angular velocity of the body (the spinning top) is
Euler equation of motion is
|
| (1) |
Where here here always refer to the angular velocity of the body axes. The angular momentum of the
body however, should add the additional spin of the body around its own body axes. This results
in
Notice the additional body spin speed added to the third component above.
And since in this case, which is due to symmetry of the body itself, the above
becomes
Taking derivative gives
From (1), Euler equation of motion of the spinning top becomes
Simplifying results in
The above are the three equations that are solved for to obtain the equations used to
simulate the spinning top. Numerical solver is used and the time step is adjusted in the simulation as needed. A
complete demonstration is build showing the motion with many different controls to allow different analysis to
be carried out on the spinning top motion.
The above equations can be put in state space formulation to allow one to use ode45 solver if needed as
follows. Let then
If using ode45, then the RHS above is what the ode45 function needs to compute.