Q1.
How to find the largest possible floating point number?
Q2. How to find the smallest
floating point number?
Q3. How to find the machine
eps?
Q4. Do I need to declare a
variable before using it?
Q6. How to remove a variable
from my workspace?
Q7. How to use symbolic
matlab to solve one equation for one unknown or N equations for N unknowns?
Q8. How to compare if 2
floating point numbers are equal?
Q9. How to numerically solve
Ax=b?
Q 10. How to multiply 2
matrices element-by-element?
Q 11. How to find the size
of a matrix?
Q 12. How to put 2 plots on
the same figure?
Q 13 How to display a table
of function values?
Q 14 How to display specific
column or row in a matrix?
Q 15 How to enter matrices
in matlab
Q 16 How to numerically ask
matlab to find a root of a function?
Q 17 How to find the minimum
of a function over some range?.
Q 18 How to numerically
solve ODE in matlab?
Q 19 How to sum elements of
an array?
Q 20 does matlab have RECORD
or STRUCT as in pascal and C?
Q 21 What is in the signal
processing tool box?
Q 22 Where to get more
matlab help?
Q 24 How to brighten or darken an image?
Q1. How to
find the largest possible floating point number?
» help realmax
REALMAX
Largest positive floating point number.
x =
realmax is the largest floating point number representable
on this
computer. Anything larger overflows.
See also
EPS, REALMIN.
» realmax
ans =
1.7977e+308
To see all the digits, type ‘vpa(realmax,320)’
Q2. How to
find the smallest floating point number?
» help realmin
REALMIN
Smallest positive floating point number.
x =
realmin is the smallest positive normalized floating point
number on
this computer. Anything smaller
underflows or is
an IEEE
"denormal".
See also
EPS, REALMAX.
» realmin
ans =
2.225073858507201e-308
Q3. How to
find the machine eps?
eps is the smallest difference between floating point
numbers that the machine can recognize. It is defined as the smallest floating
point value that when added to 1.0 will produce a floating point number
different from 1.0.
» help eps
EPS Floating point relative accuracy.
EPS
returns the distance from 1.0 to the next largest
floating
point number. EPS is used as a default tolerance by
PINV and
RANK, as well as several other MATLAB functions.
» isequal( (1+eps)-1,0)
ans =
0
» isequal( (1+eps/2)-1,0)
ans =
1
» eps
ans =
2.220446049250313e-016
%to see it in full decimal format, do
>> fprintf('%.40f',eps)
0.0000000000000002220446049250313100000000
12345678901234567890123456789012
^
|
digit 16
Q4. Do I
need to declare a variable before using it?
No. In Matlab there is no syntax for variable
declaration. When you type ‘a=10’, matlab creates the variable ‘a’ and gives it
the type ‘double’ by default.
Q5. is
matlab case sensitive?
Matlab variables and functions are case sensitive. This means variable A is different from variable a. Example:
>> clear all
>> A=10;
>> A
A =
10
>> a
??? Undefined function or variable 'a'.
Q6. How to
remove a variable from my workspace?
Use the command ‘delete’ to completely remove a variable from the workspace. For example, to remove variable called ‘a’, then type ‘delete a’. To remove all variables from workspace use the command ‘delete all’. It is a good idea to do ‘delete all’ before starting a new run of your program while testing to make sure you do not use an old variable value or the wrong variable by mistake.
Q7. How to
use symbolic matlab to solve one equation for one unknown or N equations for N
unknowns?
Use the command ‘solve’ which solves a set of
equations.
From matlab help
>> help solve
SOLVE Symbolic solution of algebraic equations.
SOLVE('eqn1','eqn2',...,'eqnN')
SOLVE('eqn1','eqn2',...,'eqnN','var1,var2,...,varN')
For example, to solve for ‘x’ in the equation
x^2+2*x+1=0, use the command
>> S=solve('x^2+2*x+1')
S =
[ -1]
[ -1]
The roots are put in a column vector S.
To solve a set of equations, say 2 equations in 2
unknowns, say x+y-4=0, 3*y+x-10=0, write
the equations each inside a string, and then write the names of the unknowns in
the order desired to get them back in the result as shown below:
S=solve('x+y-4','3*y+x-10','x','y')
S =
x: [1x1
sym]
y: [1x1
sym]
>> S.x
1
>> S.y
3
So, x=1, y=3 is the solution.
Q8. How to
compare if 2 floating point numbers are equal?
One tricky thing about using floating points is the
fact that some numbers can not be represented exactly inside the computer
hardware.
In normal math, when do ‘0.42 – 0.5 + 0.08’
the result is obviously 0. nothing more and nothing less.
But since 0.42 and 0.08 can not be represented
exactly in IEEE floating point format, we get the following wrong result from
pure mathematics point of view:
>> fprintf('%.40f', 0.42 - 0.5 + 0.08)
-0.0000000000000000138777878078144570000000
You see that the result is not the mathematical
zero.
Now, change the order of the terms, and now we get a
different result (the correct one this time)
>> fprintf('%.40f', 0.42 +0.08 - 0.5)
0.0000000000000000000000000000000000000000
Notice that the error in the first computation is
actually less the EPS (the machine accuracy tolerance):
>> fprintf('%.40f', eps)
0.0000000000000002220446049250313100000000
I’ll put EPS on top of the first result to see this
more clearly
0.0000000000000002220446049250313100000000
-0.0000000000000000138777878078144570000000
What all this means is that we need to be very
careful when we compare 2 floating points number.
If we have
N = 0.42 - 0.5
+ 0.08
M = 0.42 + 0.08 - 0.5
And we try to compare N and M above expecting to get
a result that indicates that the numbers are equal, instead we will get a
different result. This can be disastrous to the numerical application if the
algorithm we doing this comparison to decide on what logic to perform next. This
example below illustrates this:
>> N = 0.42 -
0.5 + 0.08
N =
-1.387778780781446e-017
>> M = 0.42
+0.08 - 0.5
M =
0
>> if(N==M)
disp('Numbers are equal');
else
disp('Numbers are NOT equal');
end
Numbers are NOT
equal
>>
Instead, do the floating point comparison as
follows:
>> if(
abs(N-M) < eps )
disp ('Numbers are equal');
else
disp('Numbers are NOT equal');
end
Numbers are equal
The expression
‘if
(a==b)’
should be replaced with
‘if(
abs(a-b) < eps)’
almost always when working with floating point
numbers.
So, to check if a floating point number is zero, use
‘if(
abs(a) < eps)’
The point of this is that we want to see if the
absolute difference between the 2 floating point numbers is within the EPS of
the machine. If so, then we declare these number to be mathematically equal,
even though they might have different bit pattern representation.
Q9. How to
numerically solve Ax=b?
One way is to use the ‘\’ operator. Example:
>> A=[ 1 1; -3 -6]
A =
1 1
-3 -6
>> b=[-0.5;5]
b =
-0.5
5
>> x=A\b
x =
0.666666666666666
-1.16666666666667
see also ‘pinv’ function.
Q 10. How
to multiply 2 matrices element-by-element?
If
A and B are matrices, then typing
C = A * B;
Does the normal matrix multiplication. If however
you want to multiply each element in A by the corresponding element in B
instead, then use the ‘.’ Operator as in:
C = A .* B;
For example:
>> A=[1 2; 3 4]
A =
1 2
3 4
>> B=[5 6; 7 8]
B =
5 6
7 8
>> C=A*B
C =
19 22
43 50
>> C=A .* B
C =
5 12
21 32
Q 11.
How to find the size of a matrix?
Given a matrix A, then to find the number of rows do
row = size(A,1);
To number the number of columns do
col = size(A,2);
To obtain the number of rows and number of columns
in one call do
[row,col] = size(A);
do help size for more info.
Q 12. How
to put 2 plots on the same figure?
In matlab, when you issue the command ‘plot’, it
will create a new figure window and then put the plot in that figure (assuming
no figure already exist).
When you issue the plot command again, it will erase
the earlier plot and use the same existing figure window to display the second
plot.
It is sometimes useful to display both plots on the
same figure (for example to compare one curve to the other). to do this, use
the command ‘hold on’ after the first plot command. This causes matlab to keep
the first plot (hold it on) when it plots the second plot. The command ‘hold
on’ remains in effect until you issue the command ‘hold off’. This is an
example to plot the sin(x) and cos(x) on the same figure.
>> x=[-pi:0.1:pi];
plot(x,sin(x)); hold on; plot(x,cos(x),'--')
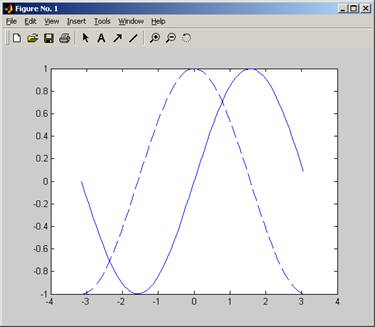
see help plot for more info.
Q 13 How to display a table of function values?
Suppose you want to display a table, that contains 2
columns. The first is the ‘x’ values and the second is the ‘y’ values. One easy
way to do this is like this:
>> x=[-pi:0.1:pi]; <--- generate the ‘x’ values
>> y=sin(x); <--- generate the ‘y’ values
>> [x' y'] <--- display side by side. Notice
the transpose
ans =
-3.14159265358979
-1.22464679914735e-016
-3.04159265358979
-0.0998334166468284
-2.94159265358979
-0.198669330795062
-2.84159265358979
-0.29552020666134
-2.74159265358979
-0.389418342308651
etc..
Q 14 How to
display specific column or row in a matrix?
Use the ‘:’
operator.
For
example, A(:,3) will be the third column of A.
A(1:3,:)
will be the first 3 rows of A
Q 15 How to
enter matrices in matlab
The following answer is copied from http://www.mines.utah.edu/~ggcmpsem/matlab/matlab.html
A good matlab tutorial.
MATLAB works with essentially only one kind of
object, ie. a rectangular numerical matrix with possibly complex entries; all
variables represent matrices. In some situations,
1-by-1 (1 x 1) matrices are interpreted as scalars and matrices with
only one row (1 x n) or one column (m x 1) are interpreted as
vectors.
Matrices can be introduced into MATLAB in several
different ways:
1.
Entered by an explicit list of elements
2.
Loaded from external data files (see User's
Guide)
3.
Generated by built-in statements and
functions
For example, either of the statements
A = [1 2
3; 4 5 6; 7 8 9]
and
A = [
1 2 3
4 5 6
7 8 9 ]
creates the obvious 3-by-3 matrix and assign it to a
variable A.
Q 16 How to
numerically ask matlab to find a root of a function?
Use the
function ‘fzero’
From help fzero:
Examples
FUN can
be specified using @:
X =
fzero(@sin,3)
returns
pi.
X =
fzero(@sin, 3, optimset('disp','iter'))
returns
pi, uses the default tolerance and displays iteration
information.
FUN can
also be an inline object:
X =
fzero(inline('sin(3*x)'),2);
Q 17 How to
find the minimum of a function over some range?
Use fminsearch.
[X,FVAL]= FMINSEARCH(...) returns the value of the
objective function,
described
in FUN, at X.
Example:
>> [h,the_min] = fminsearch(@sin,pi)
h =
4.71238898038469
the_min =
-1
Q 18 How to
numerically solve ODE in matlab?
Use matlab ode45. do help ode45. Also see on-line
demos.
See also
other
ODE solvers: ODE23, ODE113, ODE15S,
ODE23S, ODE23T, ODE23TB
options handling: ODESET,
ODEGET
output
functions: ODEPLOT, ODEPHAS2,
ODEPHAS3, ODEPRINT
evaluating
solution: DEVAL
ODE
examples: RIGIDODE, BALLODE,
ORBITODE
ODE23 and ODE45 are functions for the numerical
solution of ordinary differential equations. They employ variable step size
Runge-Kutta integration methods. ODE23 uses a simple 2nd and 3rd order pair of
formulas for medium accuracy and ODE45 uses a 4th and 5th order pair for higher
accuracy. This demo shows their use on a simple differential equation.
Q 19 How to
sum elements of an array?
From matlab on-line help:
x = [1 2 3 4 5];
<--- the sum of element is 15.
% Do add up all the elements of x, use this:
y = sum(x)
% which is better than this:
y = 0;
for i=1:length(x)
y =
y+x(i);
endy =
Q 20 does
matlab have RECORD or STRUCT as in pascal and C?
Yes.
From matlab on-line help
You can construct a structure simply by assigning
values to its fields. With these commands, we create the structure we've
depicted.
patient.name = 'John Doe';
patient.billing = 127.00;
patient.test = [79 75 73; 180 178 177.5; 172 170 169];
patient =
name:
'John Doe'
billing:
127
test:
[3x3 double]
the variable ‘patient’ is now a struct.
Q 21 What
is in the signal processing tool box?
See the on-line
help.
The Signal Processing Toolbox is a collection of tools built on the MATLAB technical computing environment. The toolbox provides two categories of tools:
Command line functions in the following categories:
1.
Analog and digital filter analysis
2.
Digital filter implementation
3.
FIR and IIR digital filter design
4.
Analog filter design
5.
Filter discretization
6.
Spectral Windows
7.
Transforms
8.
Cepstral analysis Statistical signal
processing and spectral analysis Parametric modeling
9.
Linear Prediction
10.
Waveform generation
Q 22 Where
to get more matlab help?
Matlab has an extensive on-line help.
>> help
HELP topics:
matlab\general
- General purpose commands.
matlab\ops
- Operators and special
characters.
matlab\lang
- Programming language
constructs.
matlab\elmat
- Elementary matrices and matrix
manipulation.
matlab\elfun
- Elementary math functions.
matlab\specfun
- Specialized math functions.
matlab\matfun
- Matrix functions - numerical
linear algebra.
matlab\datafun
- Data analysis and Fourier
transforms.
matlab\audio
- Audio support.
matlab\polyfun
- Interpolation and polynomials.
matlab\funfun
- Function functions and ODE
solvers.
matlab\sparfun
- Sparse matrices.
matlab\graph2d
- Two dimensional graphs.
matlab\graph3d
- Three dimensional graphs.
matlab\specgraph
- Specialized graphs.
matlab\graphics
- Handle Graphics.
matlab\uitools
- Graphical user interface tools.
matlab\strfun
- Character strings.
matlab\iofun
- File input/output.
matlab\timefun
- Time and dates.
matlab\datatypes
- Data types and structures.
matlab\verctrl
- Version control.
matlab\winfun
- Windows Operating System
Interface Files (DDE/COM)
winfun\comcli
- (No table of contents file)
matlab\demos
- Examples and demonstrations.
toolbox\local
- Preferences.
toolbox\compiler
- MATLAB Compiler
toolbox\optim
- Optimization Toolbox
signal\signal
- Signal Processing Toolbox
signal\sigtools
- Filter Design & Analysis
Tool (GUI)
signal\sptoolgui
- Signal Processing Toolbox GUI
signal\sigdemos
- Signal Processing Toolbox
Demonstrations.
toolbox\stats
- Statistics Toolbox
toolbox\symbolic
- Symbolic Math Toolbox.
MATLAB6p5\work
- (No table of contents file)
For more help on directory/topic, type "help
topic".
For command syntax information, type "help
syntax".
There are also on-line demos. Type help ‘demo’
There are zillions of matlab tutorials on the web.
Go to google and type matlab tutorial.
For example:
Mathworks own web site has the full documentation of
matlab on-line as well.
Q 23 Control system diagram
This diagram from the book signal processing using matlab
Q 24 How to brighten or darken an image?
Must convert it to double, then multiply (to brighten) by some scalar, then convert back to uint8
m=imread('Picture.png')
n=double(m(:,:,:));
n=n*2;
n=uint8(n);
image(n)