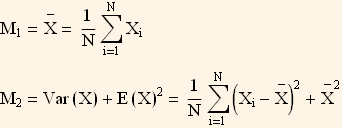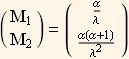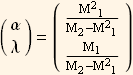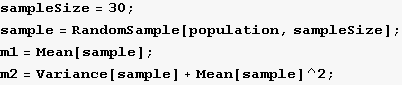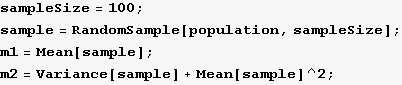A small note on the statistical method of moments for fitting a probability model to data
by Nasser Abbasi, Nov 16, 2007
Mathematics 502 probability and statistics, CSUF, Fall 2007
The problem to solve : Given some data, we seek to fit a probability law to the data. In other words, we want to determine the best probability distribution function by which the given data could have been generated according to.
We call the given data the population data. The idea of this method is as follows: Assume that the data was generated according to some distribution, say Normal or Gamma or Poisson, etc... For each one of these Choice we need to determine the relevant distribution parameters to be able to fully specify the pdf.
For example, if we want to fit the population data to the normal distribution, then we need to determine the mean and variance of the data 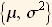 since the normal pdf is fully specified by these 2 parameters
since the normal pdf is fully specified by these 2 parameters 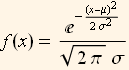
If we want to fit the population to the Gamma distribution, then we need to determine the parameters {α,λ} since the Gamma distribution is is fully specified by these 2 parameters 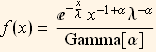 .
.
If we have to determine 2 parameters (as in the above 2 cases) then we need 2 equations. But if we wanted to fit the data to Poisson distribution, then we only need one equation since the Poisson pdf is defined in terms on one parameter λ as in f(x)=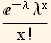
Let us assume there are n parameters to be determined (i.e. we want to fit the data to some distribution which is defined using n parameters). We call these 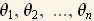 , so for the case of fitting to a normal distribution n=2,
, so for the case of fitting to a normal distribution n=2, 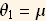 and
and 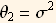 .
.
We start by writing down the n probability moments, called 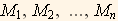 for the selected pdf we want to fit the data to. These are known analytical expressions for the selected pdf and can be looked up or derived from the assumed pdf.
for the selected pdf we want to fit the data to. These are known analytical expressions for the selected pdf and can be looked up or derived from the assumed pdf.
The 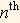 moment is defined as
moment is defined as 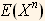 . This will give us n equations expressed as functions of the
. This will give us n equations expressed as functions of the  ,
,
Next we calculate the moments from the data itself and set these to be equal to the moments for the pdf and solve for the 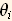 .
.
An example will help. Suppose to want to fit the data to a normal distribution, then we know that the first moment is given by 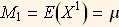 and that the second moment is given by
and that the second moment is given by  .
.
So now we have 2 equations in 2 unknowns
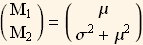
It is easier to re - write the above as follows

Now we determine an estimate for 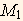 and
and 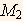 from the data, or the sample, and substitute in the above and solve for μ and
from the data, or the sample, and substitute in the above and solve for μ and 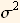
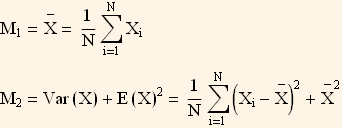
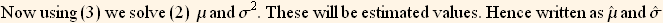
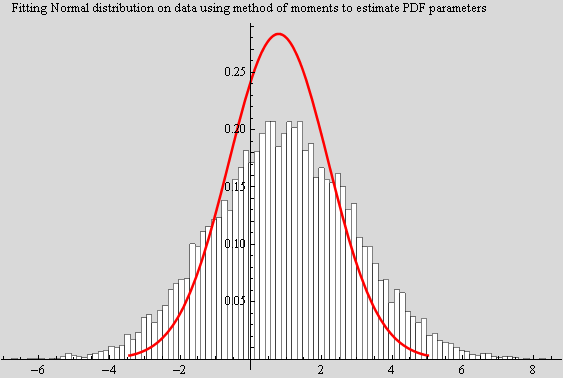
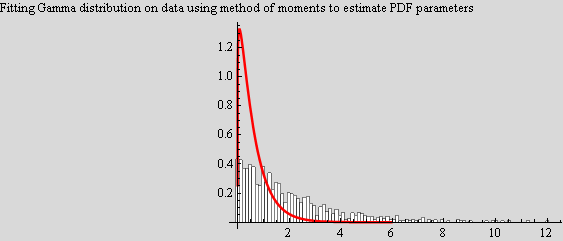
Hence the solution from above gives an estimate of the pdf parameters from the data itself. We can now plot this selected pdf using the calculated parameters on top of the histogram of the data and see how good the fit is. If the fit is not good, we can try to fit the data to a different distribution.
This is another example, suppose we have data we want to fit to a Gamma distribution, hence we know that for a Gamma distribution 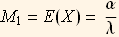 and that
and that 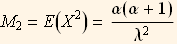 hence we have
hence we have
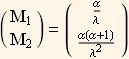
It is easier to re - write the above as follows
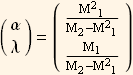
Now using (5) we solve for α and λ using the calculated values for 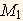 and
and 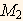 from the data as shown in (3).
from the data as shown in (3).
Numerical example
In these examples I will first generate random data (the population) from known distributions then take a small random sample from the data (with replacement), then use the method of moments above to estimate the parameters of the population (which is of course known in this case) and fit the found parameters on the population histogram to see how good the fit it.
Example 1, fitting to normal
Using real data
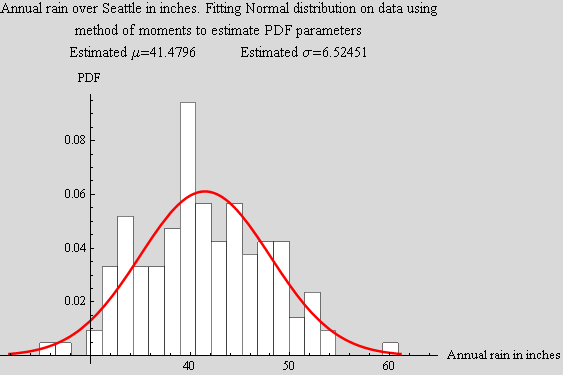
This data is the annual precipitation in Seattle (I think) for the years 1863 to 1999, it was downloaded from http://www.seattlecentral.edu/qelp/sets/049/049.html.
First load the data, and do histogram on it, then try to fit a normal distribution on it and see how good the fit is.
Load the data
In[3]:=

In[4]:=

Out[4]=
Display few lines of data
In[5]:=
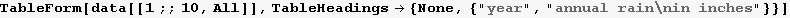
Out[5]//TableForm=
| year |
annual rain
in inches |
| 1863 |
46.31 |
| 1864 |
38.42 |
| 1865 |
49.65 |
| 1866 |
41.51 |
| 1867 |
49.94 |
| 1868 |
48.43 |
| 1869 |
45.41 |
| 1870 |
48.62 |
| 1871 |
48.84 |
| 1872 |
43.9 |
Decide on numbers of bins, and make histogram
In[6]:=

Calculate first and second moments of data
In[9]:=

Estimate data parameters. Solve the method of moments equations (this solves equations (2) above)
In[12]:=

Out[14]=
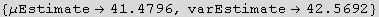
Plot the fitted PDF using the above estimated parameters
In[17]:=

Out[18]=
Using Random data
Make some random data from Normal and plot its histogram (see appendix for function to make histogram)
In[19]:=

Take a small sample with replacement and obtain the first and second moments from the sample
In[24]:=
Solve the method of moments equations (this solves equations (2) above)
In[28]:=

Out[30]=
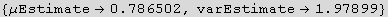
Plot the fitted PDF using the above estimated parameters
In[35]:=
Out[36]=
Example 2 fitting to Gamma
Lets try to fit a Gamma on the data to see what we get
Make some random data from Normal and plot its histogram (see appendix for function to make histogram)
In[37]:=

Take a small sample with replacement and obtain the first and second moments from the sample
In[42]:=
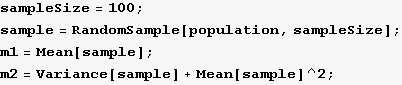
Solve the method of moments equations (this solves equations (5) above)
In[46]:=

Out[48]=

Plot the Gamma PDF using the above estimated parameters on top of the data
In[58]:=

Out[59]=
Appendix
A function to plot histogram
In[1]:=

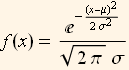
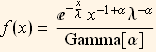 .
.