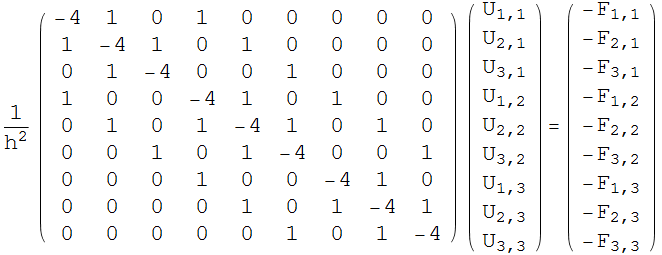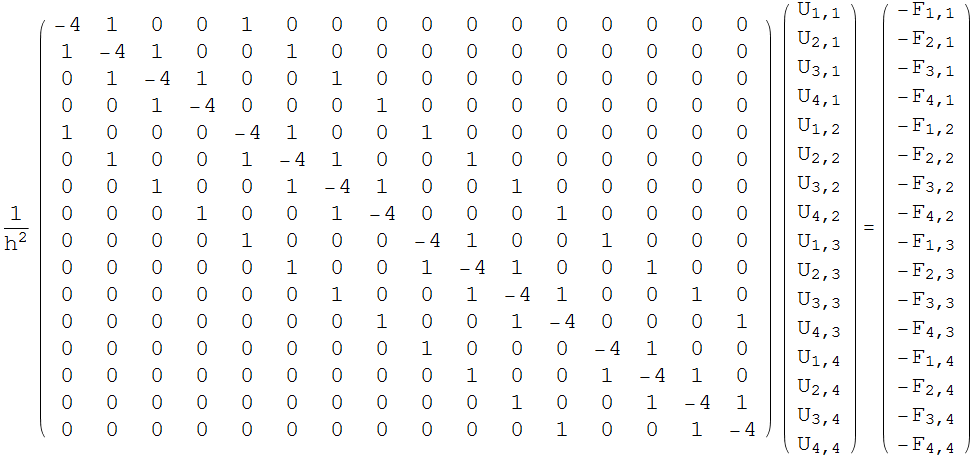Symbolic generating of system equations for 2D regular grid for solving Laplace equation using finite difference method
By Nasser M. Abbasi
updated oct 28,2010
Introduction
When solving 
) using finite difference method, in order to make it easy to see the internal structure of the A matrix using the standard 5 points Laplacian scheme, the following is a small function which generates the symbolic format of these equations for a given N, the number of grid points on one edge. At the end of this note, the system equations are generated for N=4,5,6,7,8. One can see the form of the A matrix with the dominant diagonal and the corresponding bands. It is mostly a sparse matrix.
The indexing method used is that described in the class.
Define U at each grid point
In[59]:=
Out[61]=
Define the force vector
In[62]:=
Out[63]=
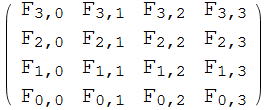
In[64]:=
In[67]:=
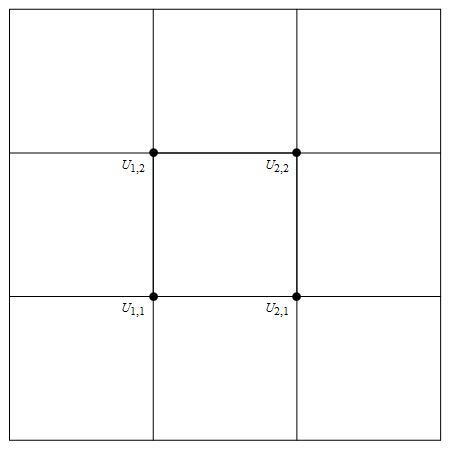
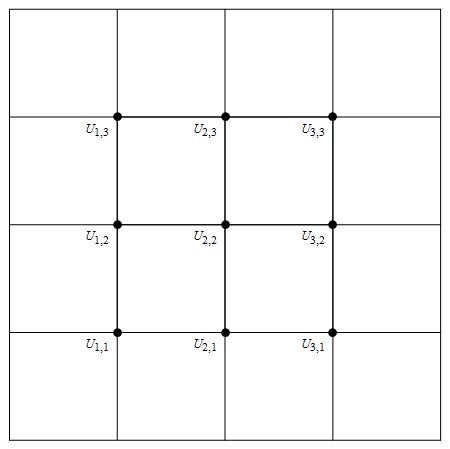
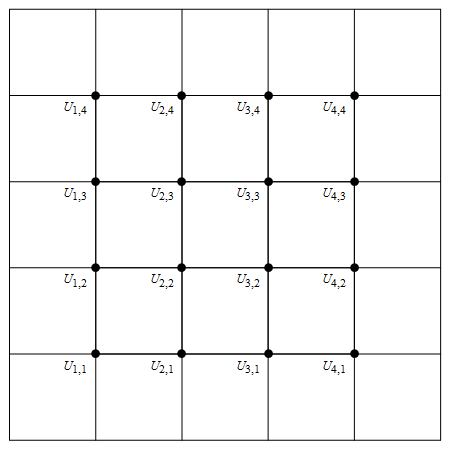
Draw the grid with the unknown above at each point
In[68]:=
Out[70]=
Generate the discrete equations at each of the internal grid points
In[71]:=
Out[72]=
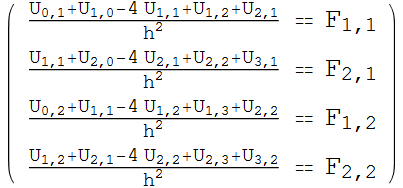
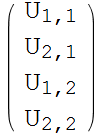
List the unknowns
In[73]:=
Out[73]=
Generate the equations of the form AU=F
In[80]:=
Out[82]=
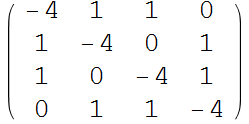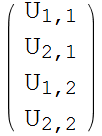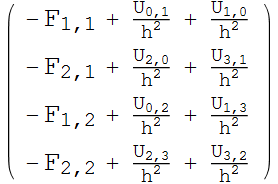For homegenous Boundary conditions
In[83]:=
Out[85]=
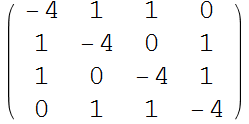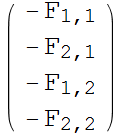set the boundary conditions. Assume left side is U=α,Right side U=β, bottom side U=γ, top side U=η, then the above becomes
In[86]:=
Display the equations again
In[90]:=
Out[90]=
Now the system can be solved for the unknowns U , given the force F values.
Below is the system equations generated for N=3,4,5,6,7,8. Put the above code into one function to use it all the time
In[91]:=
In[92]:=
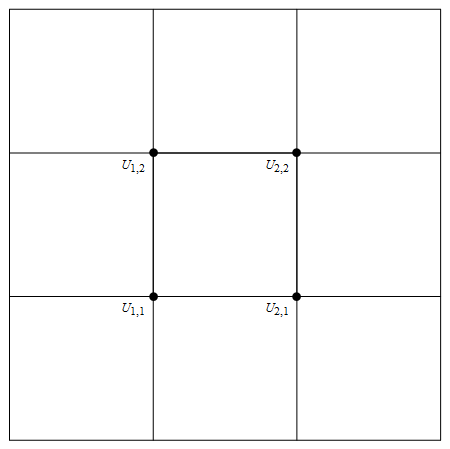
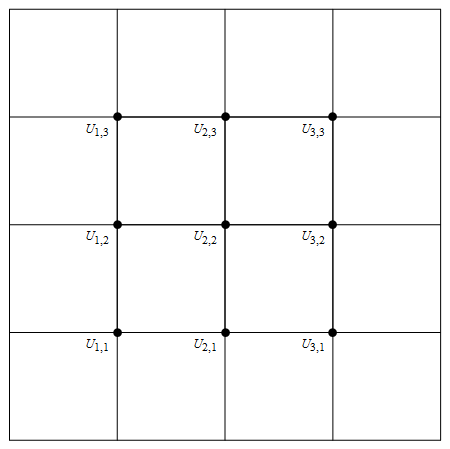
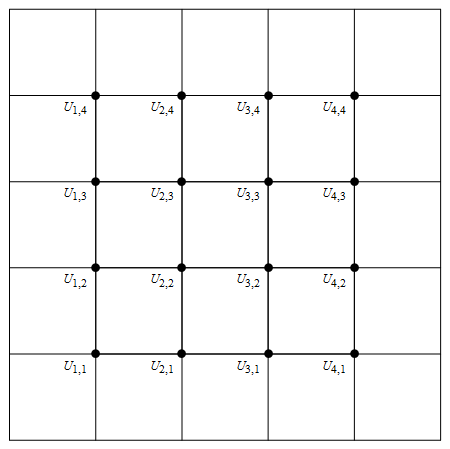
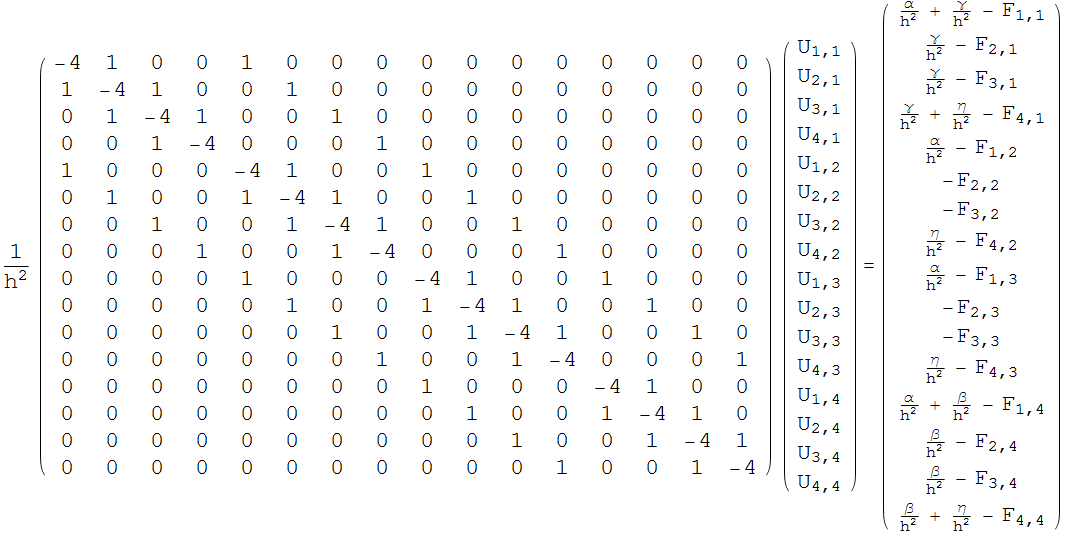
For homogenous boundary conditions
In[94]:=
