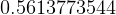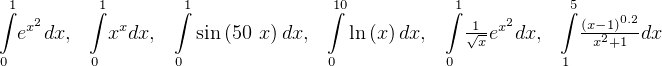
Integrate the following using Romberg integration
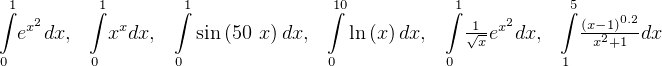
An important part is to select a tolerance which can be used to stop the Romberg iteration. This is the
tolerance shown in the pseudocode on page 212 with the letter  .
.
The source code is attached at the end, and the output.txt (in which the Romberg table is also printed for each problem).
The following is the Fortran source code to solve this HW. ??
The following is the output from running the program. ??
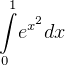
No preprocessing needed. Use Romberg integration on the integral as shown.
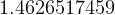
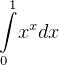
No preprocessing needed. Use Romberg integration on the integral as shown.
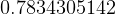
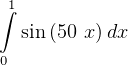
No preprocessing needed. Use Romberg integration on the integral as shown. Just make sure the tolerance is small enough. Use a multiple of machine double precision limit.
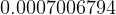
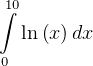
To handle the singularity at 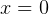 we can either integrate from some very small
we can either integrate from some very small 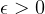 or use integration
by parts to change the integrand to something without singularity.
or use integration
by parts to change the integrand to something without singularity.
Using integration by parts. 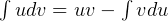 hence let
hence let 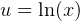 and
and 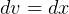 . Hence
. Hence 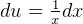
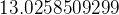 and
and
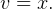
![∫10 ∫10 ( 1 ) 1∫0
(ln(x) × 1) dx = [x ln(x)]100- x -dx = [10 × ln(10)]- dx
0 0 x 0](my17x.png)
So the integral becomes
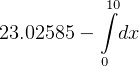
(Clearly we do not need to do numerical integration now, since the answer is 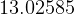 by just looking at
the above, but we need to use Romberg integration, so our integrand here is
by just looking at
the above, but we need to use Romberg integration, so our integrand here is 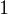 )
)
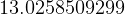
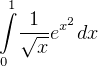
To handle the singularity at 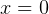 we can either integrate from some very small
we can either integrate from some very small 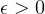 or use integration
by parts to change the integrand to something without singularity.
or use integration
by parts to change the integrand to something without singularity.
Using integration by parts. 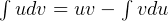 hence let
hence let 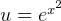 and
and 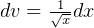 . Hence
. Hence 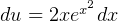
 and
and 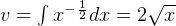
Hence
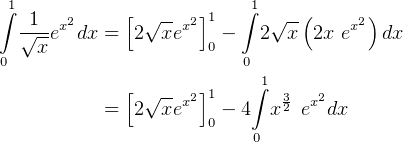
And we apply Romberg integration on the second part above.
The answer is 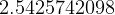
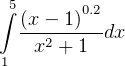
No preprocessing needed. Use Romberg integration on the integral as shown.