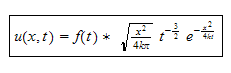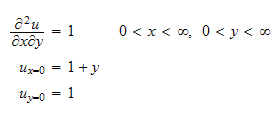
HW#7, Problem #1
UCI. MAE200B, winter 2006. by nasser Abbasi.
Problem: Solve by Laplace transform method
(a)
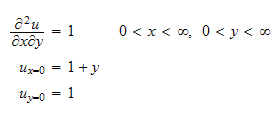
Solution for part (a)
Some definitions first. TheLaplace transform is defined as (using textbook definition)
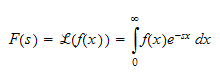
The boundary conditions are as shown:
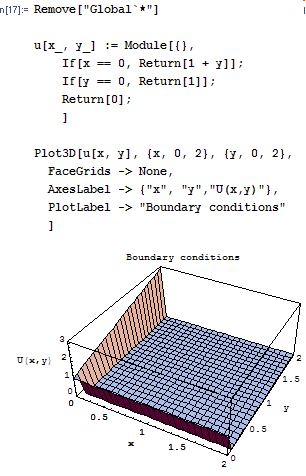
Now start the solution by assuming that
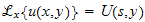 Hence
Hence
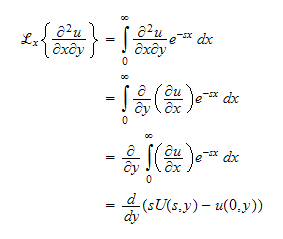
But
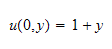
Hence
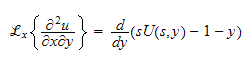
and since
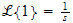 then the Laplace transform of the whole PDE is
then the Laplace transform of the whole PDE is
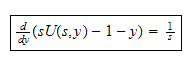
Simplify we get
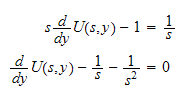
The above is like writing
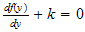 where
where
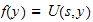 and
and
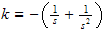 hence the solution is
hence the solution is
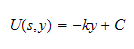
When
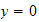 ,
,
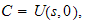 but
but
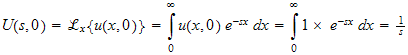 hence the above equation becomes (after replacing the constant
hence the above equation becomes (after replacing the constant
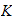 by
by
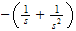 )
)
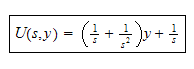
And so
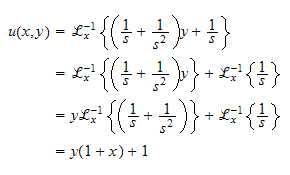
Hence the solution is
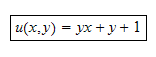
This below plots the solution above. In addition I verify the solution by solving the PDE numerically using Mathematica.

Problem: Solve by Laplace transform method
(b)
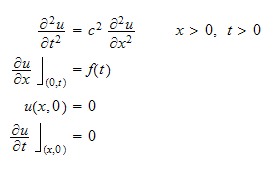
Solution for part (b)
Since
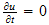 at
at
 ,
hence it is simpler to take Laplace transform w.r.t. time. Assume that
,
hence it is simpler to take Laplace transform w.r.t. time. Assume that
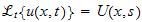 then take Laplace transform of LHS of PDE we obtain
then take Laplace transform of LHS of PDE we obtain
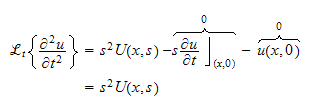
Take Laplace transform of RHS we obtain
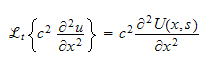
Hence putting everything together we get
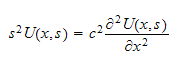
This is as if we have
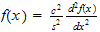 whose characteristic eq. is
whose characteristic eq. is
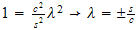
Hence the solution is
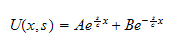 so this means the solution to eq (1) is
so this means the solution to eq (1) is
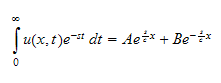
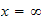
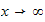
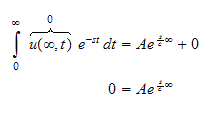
Hence
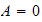
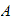 and
and
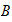 can be functions of of
can be functions of of
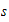 )
)
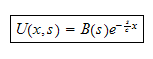
in otherwords,
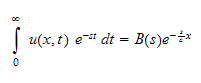
Now to be able to use the BC
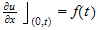 ,
we take derivative of both sides w.r.t
,
we take derivative of both sides w.r.t
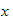 of
the above equation
of
the above equation
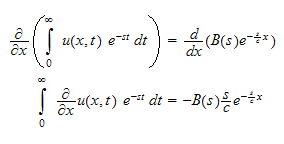
But
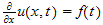 when
when
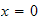 hence the above, at
hence the above, at
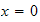 becomes
becomes
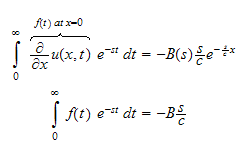
But
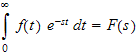 i.e. the Laplace transform of
i.e. the Laplace transform of
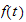 ,
hence the above becomes
,
hence the above becomes
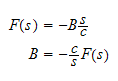
Hence equation (3) becomes
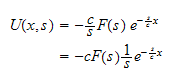
Hence the solution is obtained by taking the inverse Laplace transform w.r..t time of the above equation
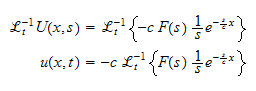
But
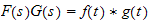 hence the above can be written as
hence the above can be written as
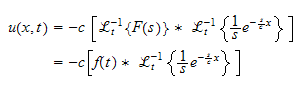
But since
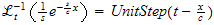 hence the above becomes
hence the above becomes
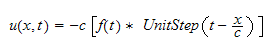
But
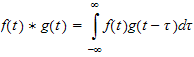 hence the above becomes
hence the above becomes
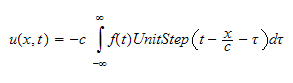
But
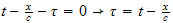 hence the above becomes (since unit step is zero before that and 1 after that)
hence the above becomes (since unit step is zero before that and 1 after that)
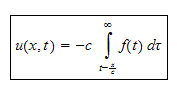
Since
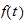 is not given, we stop here. But we note that for the solution
is not given, we stop here. But we note that for the solution
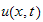 not to diverge for large time, the function
not to diverge for large time, the function
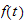 must be bounded from above for large t, something as
must be bounded from above for large t, something as
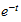 .
A function such as
.
A function such as
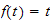 for instance will blow up the solution.
for instance will blow up the solution.
Problem: Solve by Laplace transform method
(c)
Solution for part (c)
Since
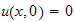 ,
hence it is simpler to take Laplace transform w.r.t. time. Assume that
,
hence it is simpler to take Laplace transform w.r.t. time. Assume that
 then take Laplace transform of PDE we obtain
then take Laplace transform of PDE we obtain
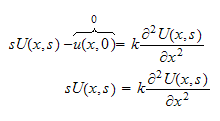
This is like
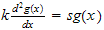 whose characteristic equation is
whose characteristic equation is
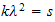 hence
hence
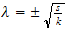 hence the solution is
hence the solution is
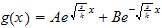 in otherwords
in otherwords
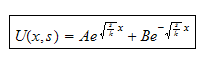
so this means
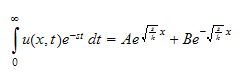
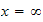
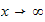
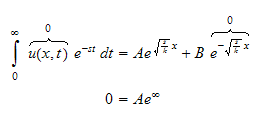
Hence
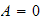 so equation (1) becomes
so equation (1) becomes
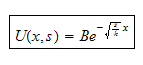
Now the above can be written as
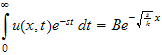 ,
and now use the BC that
,
and now use the BC that
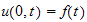 hence the above becomes
hence the above becomes
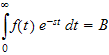 in other words,
in other words,
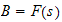 where
where
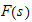 is laplace transform of
is laplace transform of
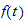 ,
hence the solution now becomes
,
hence the solution now becomes
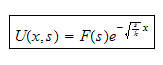
Take inverse laplace, we obtain
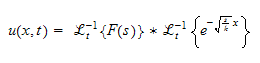
But
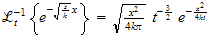
so