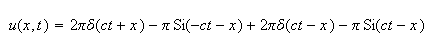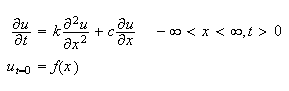
Problem #5

UCI. MAE200B, winter 2006. by nasser Abbasi.

Problem: Solve the following problems by transform methods

(a)

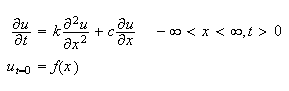
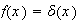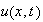Consider the special case when . Sketch the corresponding for various values of .

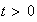Solution for part (a)

Some definitions first. The Fourier transform is defined as (using textbook definition)

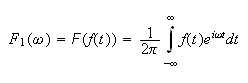
and the inverse Fourier transform is

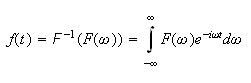
And the convolution is defined as

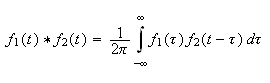
The shift property:

If has Fourier transform then 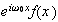has the Fourier transform

The delay property:

If 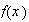has fourier transform 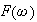then 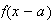has fourier transform

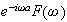
If 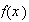has fourier transform 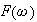then 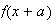has fourier transform

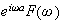
and

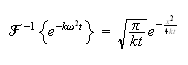
And the property of differentiation

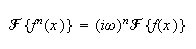
Now start the solution by assuming that

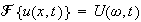
Start by taking the fourier transform of each term in the PDE w.r.t 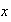, and assume that

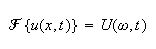
and assume that the fourier transform of 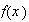is

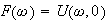
Hence

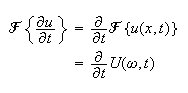
and

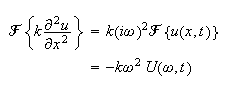
and

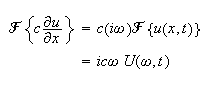
Now take the fourier transform of the PDE and using the above relations

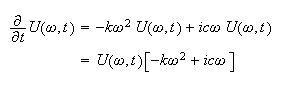
Hence this is now a first order ODE, the solution is

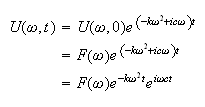
To find the solution 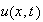then take the inverse fourier transform of the above

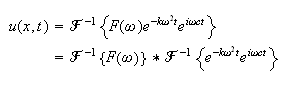
Using the delay property we get

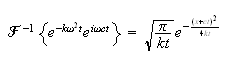
Hence the solution is

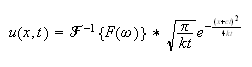
When 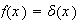, 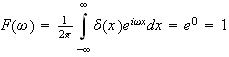hence

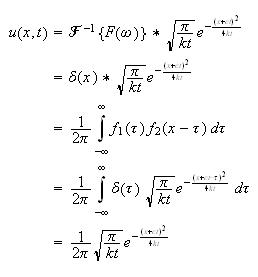
Hence the solution is

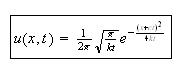
The effect of the term 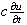is to introduce the term 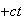in the exponential as shown above. 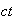has units of distance, so the term 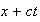acts as a shift in distance. So it is a transport phenomena. I.e. diffusion with mass transport.

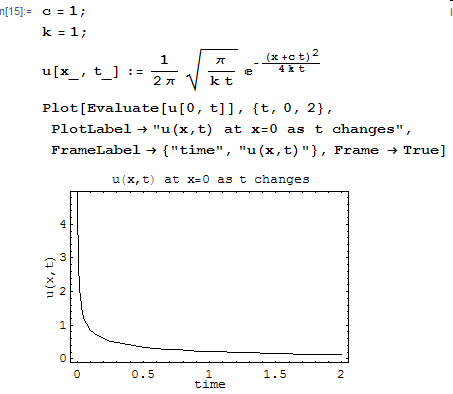
This is a plot of the solution, I picked 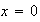where the dirac delta function is to show how 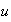changes with time at that location.

Problem: Solve the following problems by transform methods

(b)

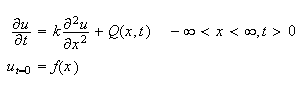
Solution for part (b)

Start by taking the fourier transform of each term in the PDE w.r.t 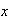, and assume that

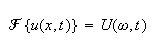
and assume that the fourier transform of 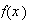is

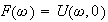
Hence

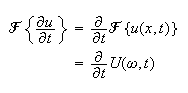
and

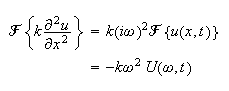
Now take the fourier transform of the PDE w.r.t 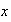and using the above relations

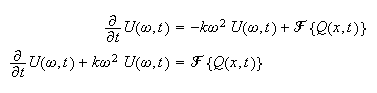
Hence this is now a first order ODE, nonhomogeneous. Star by solving the homogeneous ODE. The solution is

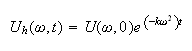
To find the solution 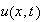then take the inverse fourier transform of the above

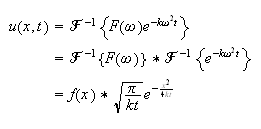
I am not sure if we should assume that 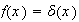as well as part(a) as the problem was not clear. To precessed, I assume so, else not knowing what 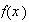is one can not do anything more here.

When 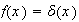, 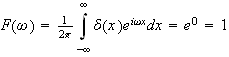hence

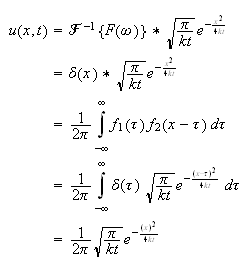
Hence the homogeneous solution is

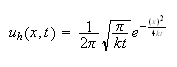
Not knowing what is, assume that the particular solution is which can be found by using method of finding integrating factors, hence the solution is

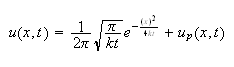
Problem: Solve the following problems by transform methods

(c)

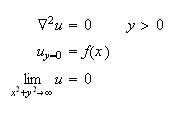
Solution for part (c)

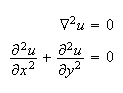
Take fourier transform w.r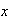.t , assume that

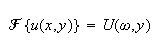
Take fourier transform of the PDE we obtain

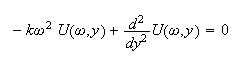
This is a second order ODE, the characteristic equation is

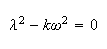
solution is

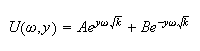
Using the second B.C. that 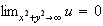, this implies that 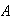must be zero, else 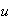will not vanish as 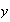goes to 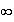. Hence we obtain

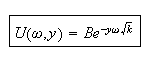
Hence

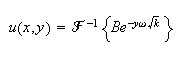
But

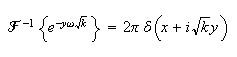
Hence (1) becomes

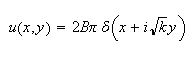
at , 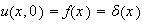hence

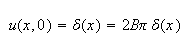
Hence

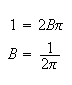
So the solution is

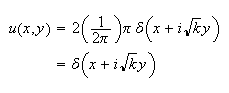
Problem: Solve the following problems by transform methods

(d)

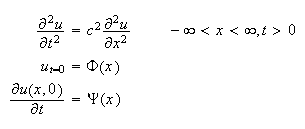
Solution for part (d)

Taking Fourier transform w.r.t

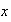
assume that

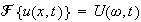
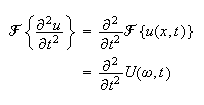
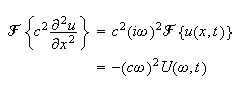
Hence the PDE becomes

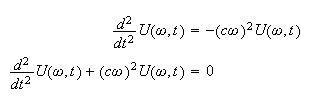
This is a second order ODE. The characteristic equation is

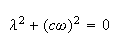
Hence

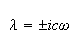
Hence the solution is

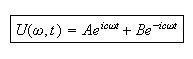
Apply BC, at

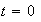
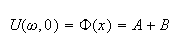
Apply second BC

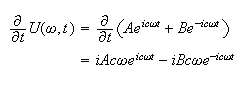
at 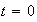, 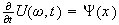hence

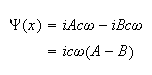
Hence we have 2 equations

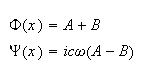
Solve for A,B

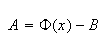
Hence

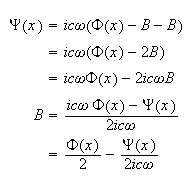
and

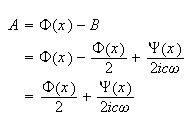
Hence solution is

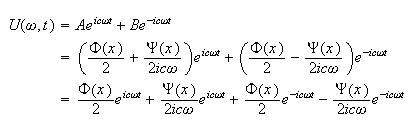
Hence

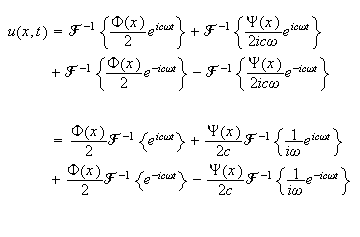
But

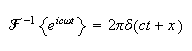
and

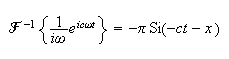
Where 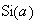is the sign function which gives -1, 0 or 1 depending on whether 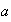is negative, zero, or positive

and

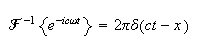
and

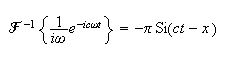
Hence