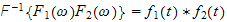
Problem #4

UCI. MAE200B, winter 2006. by nasser Abbasi.

Problem: Prove the convolution theorem for the Fourier transform

Solution

Some definitions first. The Fourier transform is defined as (using textbook definition)

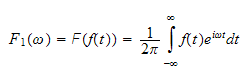
and the inverse fourier transform is

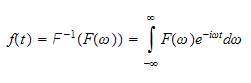
And the convolution is defined as

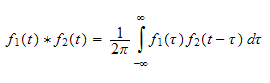
Start the proof by showing that 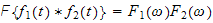, this implies that

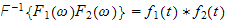
So, take the fourier transform of the convolution, we obtain

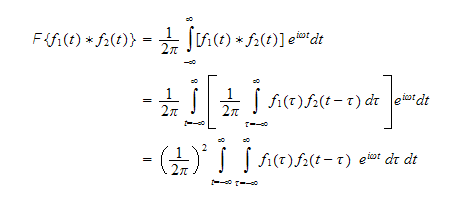
Let 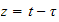, hence 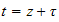, and so 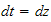. When 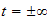, 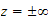and the above can be written as

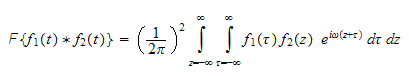
Exchange the integrals order we obtain

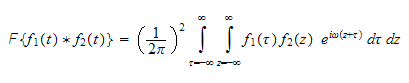
Break the exponential into product of 2 exponential

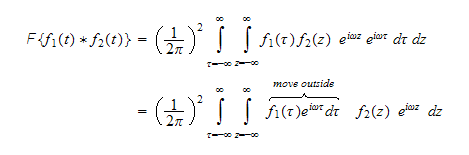
We can now move the marked terms outside the inner integral since they do not depend on

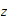
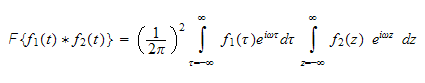
But by definition 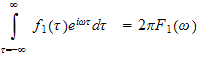and similarly 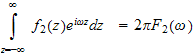, hence eq (1) can be written as

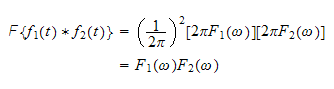
This results means that

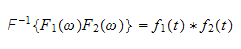
This completes the proof. (We should also proof the other direction since this is an IFF problem, i.e. starting from 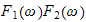take its inverse fourier transform we would get the convolution). But I think this proof done here should be sufficient.