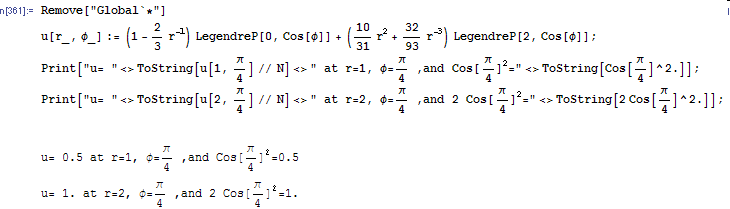 and
and
 with the following boundary conditions
with the following boundary conditions
Problem #3
UCI. MAE200B, winter 2006. by nasser Abbasi.
Problem: Harmonic function in a spherical shell. Find the
solution to the Laplace equation in a spherical shell bounded between
 and
and
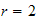 with the following boundary conditions
with the following boundary conditions
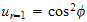 ,
,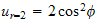 where
where
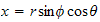 ,
,
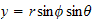 and
and
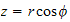
Solution
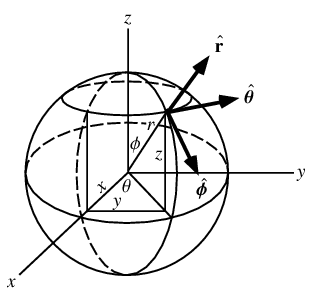
The laplacian in spherical coordinates is
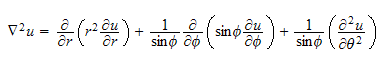
Since the boundary conditions depends on
 only, then the solution will not depend on
only, then the solution will not depend on
 and hence the PDE simplifies to
and hence the PDE simplifies to
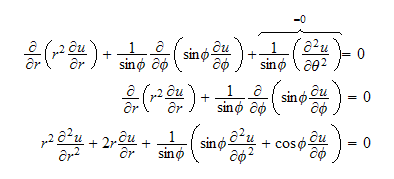
Assume
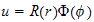 ,
and substitute in the above PDE, we obtain
,
and substitute in the above PDE, we obtain
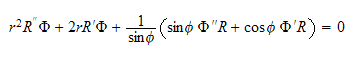
divide by
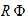 and rearrange
and rearrange
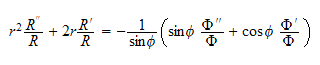
The LHS depends on
 only and the RHS depends on
only and the RHS depends on
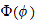 and hence we apply separation of variables by setting both side equal to same
constant. Call this constant
and hence we apply separation of variables by setting both side equal to same
constant. Call this constant
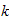 for now (Later we will see that
for now (Later we will see that
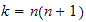 for integer
for integer
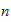 ).
Hence
).
Hence
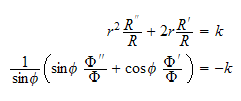
hence we obtain the following 2 differential equations to solve
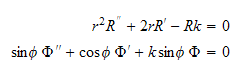
Looking at equation (2) for now, which we can write as
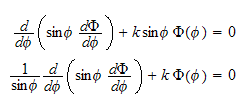
Now make the substitution
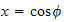 ,
hence
,
hence
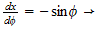
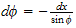
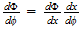 hence
hence
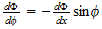
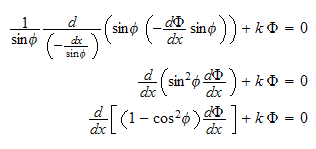
But since
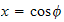 , the above can be written as
, the above can be written as
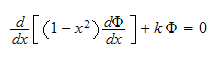
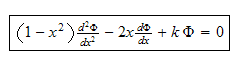
equation (4) is the Legendre differential equation when has solution only for
integral values of
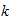 ,
and these values must be successive, hence we write
,
and these values must be successive, hence we write
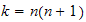
 for
integer
for
integer
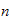 ,
and the solution to (4) becomes the Legendre polynomials
,
and the solution to (4) becomes the Legendre polynomials
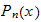 for
for
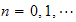 but since
but since
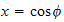 then the solution to equation (2) is
then the solution to equation (2) is
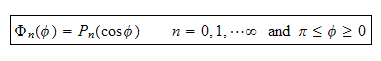
Now the
 equation, equation (1), can be written by replacing
equation, equation (1), can be written by replacing
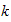 in terms of the eigenvalues
in terms of the eigenvalues
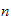 as
as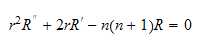
Equation (5) is the Euler differential equation. This equation has the
solution
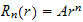 and
and
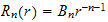 Hence
Hence
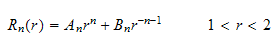
Hence the overall solution
is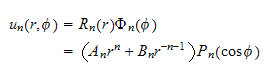
so
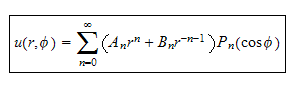
Applying B.C. at
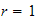 and
and
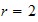 we obtain the following 2 equations
we obtain the following 2 equations
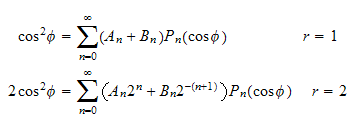
Hence apply the inner product on each equation to evaluate the coefficients,
we obtain the following 2 equations (note that the weight is
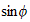 when expressed in terms of
when expressed in terms of
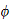
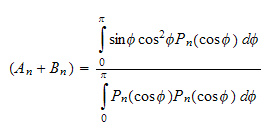
Lets call the integral
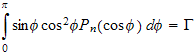 , and given that
, and given that
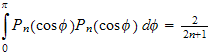 hence
we write the above as
hence
we write the above as
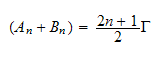
And for the BC at
 we obtain
we obtain
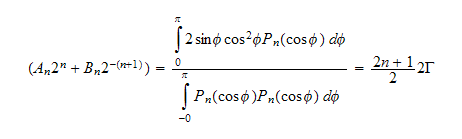
Hence
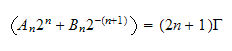
Now we need to solve eq (6) and eq (7) for
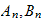
From (6)
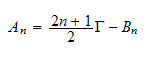
Substitute into (7) we obtain
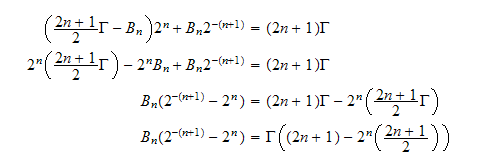
Hence
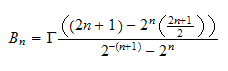
Substitute the above value for
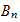 in (6) to find
in (6) to find
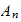
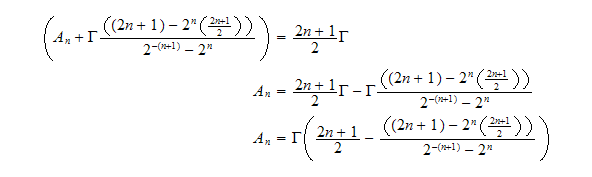
Hence finally we have
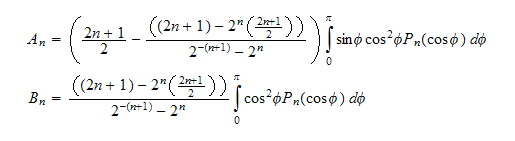
The following script prints few values of
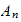 and
and
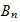
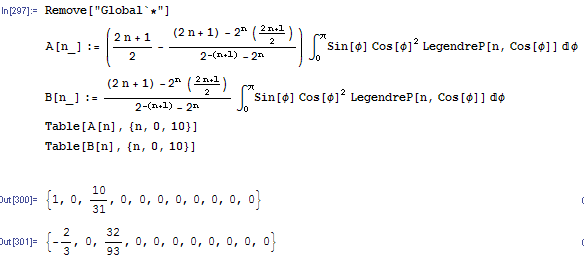
We see that
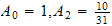 and all other
and all other
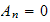 and that
and that
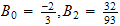 and all other
and all other
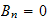
Hence the solution is
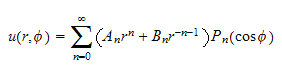
so given the above coefficients, we obtain the final solution as
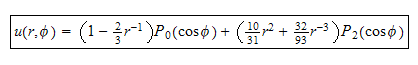
To verify, pick some
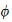 and let
and let
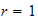 and
and
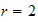 and verify the boundary conditions. This scripts verifies that the solution is
correct.
and verify the boundary conditions. This scripts verifies that the solution is
correct.