
HW 1, MAE 200B.
Problem 2
by Nasser Abbasi
UCI, Winter 2006.
Question

Solution
This is a heat conduction PDE with 3 spatial dimensions and one in time. Hence
the PDE is
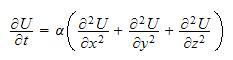
Use method of separation of variables to solve.
Assume
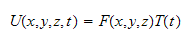
Where the function
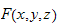 depends on the spatial dimensions only and the function
depends on the spatial dimensions only and the function
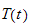 depends on time only. Substitute eq(2) into (1) we get
depends on time only. Substitute eq(2) into (1) we get
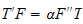 or
or
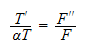
Hence as we reasoned in the first problem, since the LHS of eq(3) depends on
time only and the RHS depends on the spatial coordinates only, then we way
that each side of eq. (3) must be equal to a constant, say
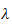 ,
hence eq (3) can be written as
,
hence eq (3) can be written as
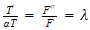 from which we obtain 2 equations to solve
from which we obtain 2 equations to solve
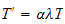 and
and
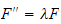
The second of the above equations,

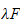 or
or
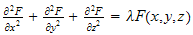 is called the Helmholtz equation. To solve, we again assume that
is called the Helmholtz equation. To solve, we again assume that
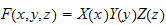 where
where
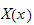 is a function of
is a function of
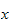 only, and
only, and
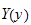 is a function of
is a function of
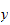 only and
only and
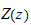 is a function of
is a function of
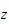 only. And now we substitite back in the Helmholtz equation and we get
only. And now we substitite back in the Helmholtz equation and we get
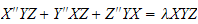 ,
and divide by
,
and divide by
 we obtain
we obtain
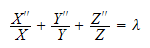
In eq(4), We apply separation of variables again to obtain 3 ODE's each for
 and
and
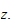 (4) can be written as
(4) can be written as
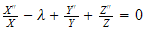 or
or
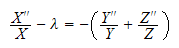 hence we see that the LHS depends on
hence we see that the LHS depends on
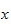 only and the right hand side does not depend on
only and the right hand side does not depend on
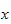 and both are equal to each others, then they must be both equal to the same
constant, say
and both are equal to each others, then they must be both equal to the same
constant, say
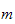 ,
hence we obtain that
,
hence we obtain that
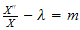 and
and
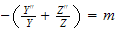
From
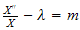 we get
we get
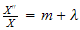 or
or
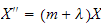
 and
now since
and
now since
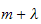 is a constant, call it
is a constant, call it
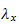 hence the ODE is
hence the ODE is
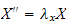 whose solution is
whose solution is
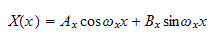 where
where
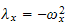 for some positive constant
for some positive constant
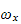
Now that we obtained solution for
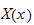 we go back and obtain solutions for
we go back and obtain solutions for
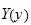 and
and
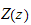 .
From equation (5) we have
.
From equation (5) we have
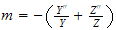 or
or
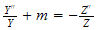 hence since the LHS depend on
hence since the LHS depend on
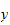 only and the RHS depends on
only and the RHS depends on
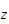 only and they both equal, then they must be equal to some constant, say
only and they both equal, then they must be equal to some constant, say
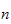 hence we obtain that
hence we obtain that
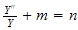 and
and
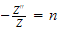
Looking at the
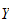 equation, we obtain
equation, we obtain
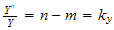 or
or
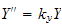 which has solution
which has solution
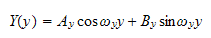
where
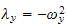
And from the equation
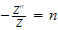 we obtain the solution as
we obtain the solution as
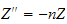 or
or
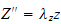 whos solution is
whos solution is
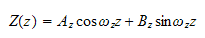
where
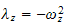
So, to summarise we have now 4 ODE's to solve, which are