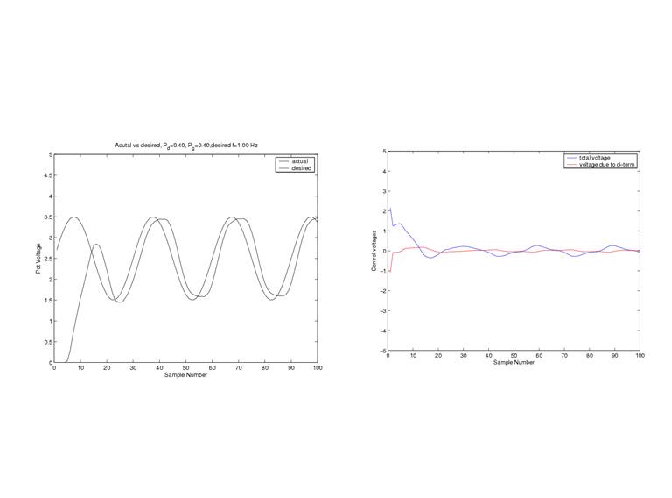
 Hz. This plot below shows few of the tests I've run, and below them the one
I think achieved the best tracking.
Hz. This plot below shows few of the tests I've run, and below them the one
I think achieved the best tracking.
LAB #7 report. MAE 106. UCI. Winter 2005
Nasser Abbasi, LAB time: Friday 2/25/2005 10 AM
I have tried a number of runs with different proportional and derivative gain
constants running at
 Hz. This plot below shows few of the tests I've run, and below them the one
I think achieved the best tracking.
Hz. This plot below shows few of the tests I've run, and below them the one
I think achieved the best tracking.
Derivative gain=0.4
Proportional
gain=0.4

First I need to derive the transfer function. I can decide to control the speed of the motor shaft, or its angular position. I need to decide on this since this affect what the transfer function will be. i.e. wither I will select the position or the speed to be the output. In both cases I will take the motor voltage supply as the input.
I selected to use position as the controller variable.
First, I show the model of the motor itself, then the block diagram. Next I show the block diagram with a delay element added in the feedforward path, and the compare the transfer functions with and without delay and show that with delay, it is possible for the output to become unstable.
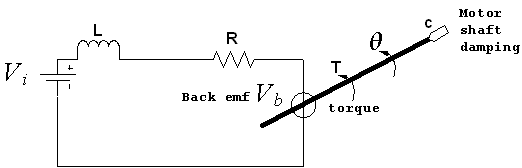
From the diagram below, using Kirchoff law around the motor circle, we get
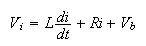
Take Laplace transform we get
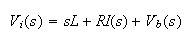
Now, we know that the backemf voltage
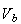 produced is proportional to the angular speed of the shaft. Let this
proportionality constant be called
produced is proportional to the angular speed of the shaft. Let this
proportionality constant be called
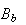 then
we write
then
we write
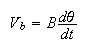
Take Laplace transform of the above, we get
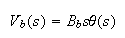
Substitute equation (2) into (1) we get
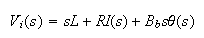
Now consider the dynamic equation for the motor shaft, we get
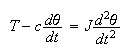
Where
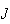 is the moment of inertial of the motor shaft around its axis of rotation. Take
Laplace transform of the above we get
is the moment of inertial of the motor shaft around its axis of rotation. Take
Laplace transform of the above we get
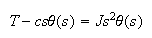
We also know that the torque produced is proportional to the current in the
motor. Lets call the proportionality constant
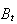 hence we write
hence we write
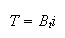
Take Laplace transform of (5) we
get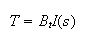
Substitute (6) into (4) we get
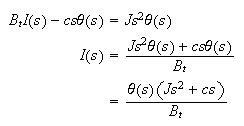
Now substitute (7) into (3) we get
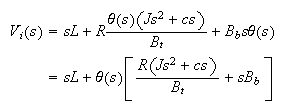
Now
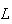 is usually very small compare to
is usually very small compare to
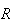 so equation (8) can be written as
so equation (8) can be written as
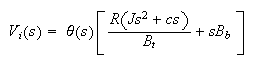
Hence the transfer function between
 and
and
 is
is
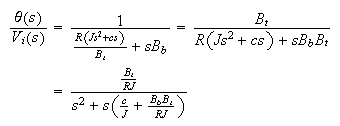
This transfer function is in the standard form. It is a second order system.
The above is the transfer function of the plant itself. Now I put the above
into the loopback block diagram, assuming the controller we used is PD
controller of the form
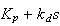 we get
this
we get
this
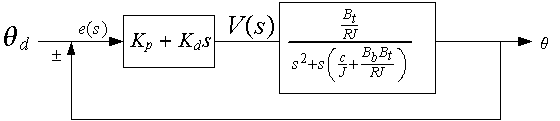
Now we do block simplification to obtain the closed loop transfer function.
Let
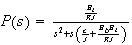 ,
hence the feedforward transfer function is
,
hence the feedforward transfer function is
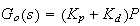 hence the closed loop transfer function is
hence the closed loop transfer function is
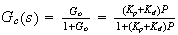
Let
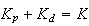 then we write
then we write
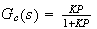
The charaterstic equation is
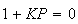 .
The closed loop poles are the roots of this equation.
.
The closed loop poles are the roots of this equation.
Replace
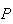 above to be able to solve for the roots, we get
above to be able to solve for the roots, we get
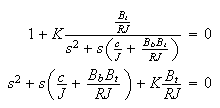
the roots are
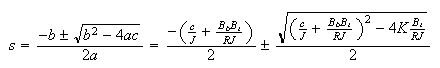
We see from the above, that independent of the values under the
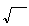 sign,
the system will have its poles in the left hand side. This is because the
quantity
sign,
the system will have its poles in the left hand side. This is because the
quantity
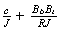 is positive.
is positive.
Hence the system is always stable no matter how large the gain
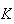 is.
is.
Now let see what happens when we add the effect of Labjack into the system,
model this effect as a time delay, which in the Laplace transform becomes
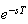 where
where
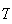 is the time it takes Labjack to sample one data point, i.e.
is the time it takes Labjack to sample one data point, i.e.
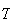 is the sampling period. Hence now the block diagram
becomes
is the sampling period. Hence now the block diagram
becomes

Where I wrote
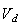 as the output from the labjack. (delayed voltage).
as the output from the labjack. (delayed voltage).
Now, since
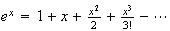
Then
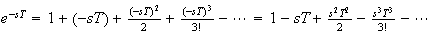
Now for very small
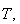 all terms with
all terms with
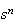 for
for
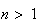 can be ignored. Hence we get an approximation
can be ignored. Hence we get an approximation
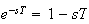
Hence the above system
becomes

Now obtain the closed loop transfer function.
The open loop transfer function is
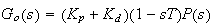
As before, let
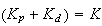 ,
hence we get
,
hence we get
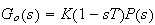
Then the closed loop transfer function is
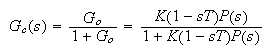
The characteristic equation is
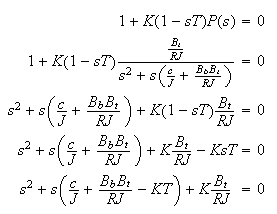
The roots of this equation (i.e. the poles of the closed loop) now can be found as
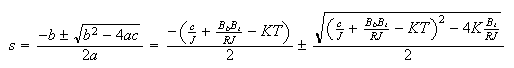
Now we clearly see the effect of the delay of the closed loop poles.
We see that the real part of the pole can occur at the positive side of the s
plane, and this will happen when
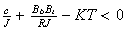 or when
or when
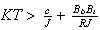
hence we see that as
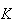 is increased, the closed loop pole will move to the right until it will cross
the imaginary axes making the system unstable. In addition, for a fixed gain
is increased, the closed loop pole will move to the right until it will cross
the imaginary axes making the system unstable. In addition, for a fixed gain
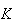 ,
as
,
as
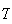 is increased the system can become stable. An increase in
is increased the system can become stable. An increase in
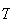 implies that the sampling frequency becomes smaller, since
implies that the sampling frequency becomes smaller, since
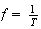 .
.
This is what we are asked to show.