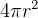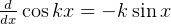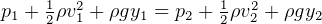
Bernulli
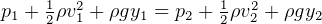
continuity equation
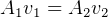
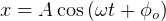
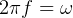
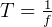
we can find 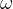 from:
from:
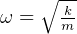
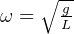
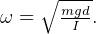 where d is distance from center of mass to pivot, and I is
moment of inertia. For a rod,
where d is distance from center of mass to pivot, and I is
moment of inertia. For a rod, 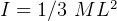
Parallel axis theorm: moment of interia=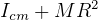
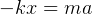
solution is 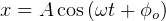
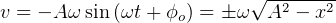 (use this form if given x and A and asked to find v)
(use this form if given x and A and asked to find v)
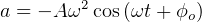
Total energy in a spring = 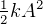 where A is the amplititude.
where A is the amplititude.
KE+PE=total energy.
KE=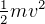
PE=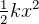
retadring force 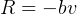
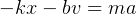
Solution is 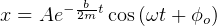 where
where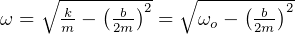
There are 3 cases of damped oscillations:
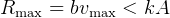
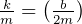 i.e.
i.e. 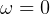
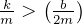
Assume we apply a force 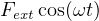 , in addition to damping force
, in addition to damping force 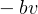 ,hence the ODE now
is
,hence the ODE now
is
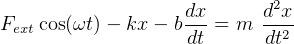
Solution is 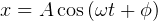 where
where 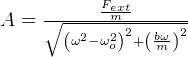 where
where 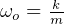
We see that as 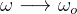 then
then 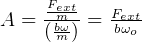 ,Now in the absense of damping force, this means
,Now in the absense of damping force, this means 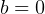 ,
then we see that
,
then we see that 
For springs in series, 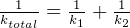 , so
, so 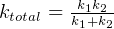
For springs in parallel. 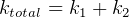
see printout
see printout
see printout
If the path difference 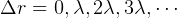 then the result sum of the waves is constructive (more amplitude). If
then the result sum of the waves is constructive (more amplitude). If
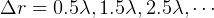 then the result is destructive.
then the result is destructive.
In a pipe, which is open on one end and closed on the other end, we can only have the fundamental
harmoic, then the 3rd then the 5th, etc... i.e. we skip the second and the fourth, etc.... so we get
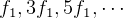 . here,
. here, 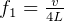
If closed (or open) on both ends, i.e. we have standing waves, then we get 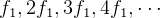 . here,
. here,
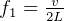 wher
wher 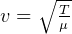 or
or 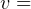 speed of sound depending on instrument.
speed of sound depending on instrument.
given  and
and 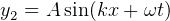 i.e. same waves but travelling towards each others (i.e. in
opposit directions), their sum is
i.e. same waves but travelling towards each others (i.e. in
opposit directions), their sum is 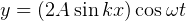
In a standing wave (both ends are closed) and when the waves are in phase, and have the same frequency and amplitude, then the locations of the nodes and antinodes are given by
nodes: 
antinodes: 
So, to find locations of nodes/antinodes, simply calculate 
Also, we can write 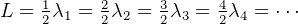 we can use this to find L if given two different and
successive
we can use this to find L if given two different and
successive 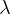
Diffraction is the divergence of light from its initial line of travel (as it leaves a slit). To see diffraction use single slit. (to see interference of light, use 2 slits).
For diffraction, slit width is used. For interference, distance between slits is used.
The angle 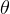 at which dark bands are seen on the screen is found from
at which dark bands are seen on the screen is found from 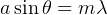 , where
, where
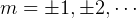
Also notice that the central maxiumum band is twice as wide as the second maxima.
To find intensity at different maxima and minima use this:
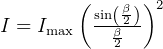 here,
here, 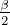 is the phase difference
is the phase difference
where 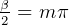 ,
, 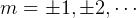 for minima (we get I=0)
for minima (we get I=0)
and 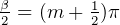 ,
, 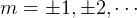 for maxima (we get I=0)
for maxima (we get I=0)
For example, for 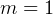 , maxima intensity is found
, maxima intensity is found
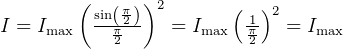
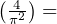
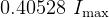
for 
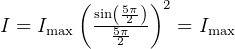
for 
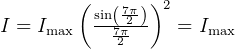
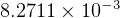
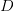
For angular resolution of 2 sources, use 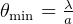 where
where 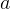 is the width of the slit.
is the width of the slit.
If the slit was circular, with diameter 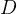 then
then 
Diffraction granting is used to resolve/find wave length.
Resolving power 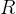 of a diffracting granting is
of a diffracting granting is 
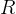 is also given by
is also given by 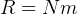 , where
, where 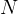 is the number of lines/grids, and
is the number of lines/grids, and 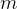 is the order number.
is the order number.
Polrization: 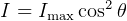
Polarization by relfection: When tan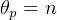 , then reflected light is polarized.
, then reflected light is polarized.
One course, but 2 slits. Hence, we consider the light comming from the slits as 2 coherent sources (since from
the same original source). (So, same frequency 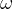 and the same amplitude
and the same amplitude 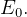
Now, as rays leave the slits, they travel different directions. And the path difference travelled causes a phase
difference between the rays. Let this pahse difference be 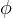
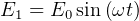
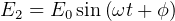
So, 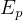 which is
which is 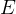 at point p on the screen is given by
at point p on the screen is given by 
Intensity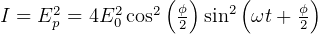
time averaged intensity is 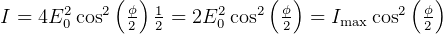
where 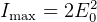
Notice that here, 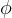 is the phase difference between the 2 rays measure AT THE WALL.
is the phase difference between the 2 rays measure AT THE WALL.
we see that when phase difference is 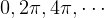 then we get a maxima. When phase difference is
then we get a maxima. When phase difference is
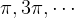 we get a minima
we get a minima
We can find phase difference 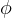 given angle
given angle 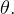 since
since 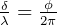
this leads to 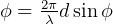
This leads to 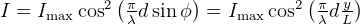
So, this gives the intensity at hight 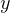 from the center.
from the center.
From this we see that 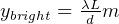 for
for 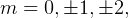
and 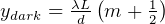 for
for 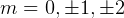
If given wave length 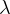 in vacume, and given a matrial whose index of refraction
in vacume, and given a matrial whose index of refraction 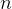 , then the wave length
in the matrial is found from
, then the wave length
in the matrial is found from 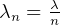
area of circle 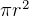
circumferance of circle 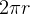
area of sphere: