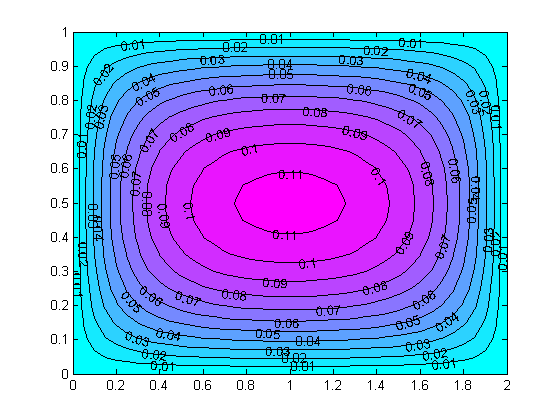
clear;
format long;
fc=1;
bc=0.;
W=1;
L=2.0;
N=20;
M=40;
dx = L/M;
dy = W/N;
D=(N+1)*(M+1);
s=zeros(D,D);
f=zeros(D,1);
v=zeros(N+1,M+1);
xindex=0;
yindex=0;
x1=0; x2=0; x3=0; x4=0;
j1=0; j2=0;
for yindex = 1:N
for xindex = 1:M
x1 = xindex + (yindex-1)*(M+1);
x2 = 1+ x1;
x3 = xindex + yindex*(M+1);
x4 = 1+ x3;
j1 = dx*dy;
s(x1,x1) = s(x1,x1)+(dx^2+dy^2)/(2*j1);
s(x1,x2) = s(x1,x2)-dy^2/(2*j1);
s(x1,x3) = s(x1,x3)-dx^2/(2*j1);
s(x2,x1) = s(x2,x1)-dy^2/(2*j1);
s(x2,x2) = s(x2,x2)+dy^2/(2*j1);
s(x2,x3) = s(x2,x3);
s(x3,x1) = s(x3,x1)-dx^2/(2*j1);
s(x3,x2) = s(x3,x2);
s(x3,x3) = s(x3,x3)+dx^2/(2*j1);
f(x1,1) = f(x1,1)+ fc*j1/6;
f(x2,1) = f(x2,1)+ fc*j1/6;
f(x3,1) = f(x3,1)+ fc*j1/6;
j2 = dx*dy;
s(x4,x4) = s(x4,x4)+(dx^2+dy^2)/(2*j2);
s(x4,x2) = s(x4,x2)-dx^2/(2*j2);
s(x4,x3) = s(x4,x3)-dy^2/(2*j2);
s(x2,x4) = s(x2,x4)-dx^2/(2*j2);
s(x2,x2) = s(x2,x2)+dx^2/(2*j2);
s(x2,x3) = s(x2,x3);
s(x3,x4) = s(x3,x4)-dy^2/(2*j2);
s(x3,x2) = s(x3,x2);
s(x3,x3) = s(x3,x3)+dy^2/(2*j2);
f(x4,1) = f(x4,1)+ fc*j2/6;
f(x2,1) = f(x2,1)+ fc*j2/6;
f(x3,1) = f(x3,1)+ fc*j2/6;
end
end
for xindex=1:M+1
s(xindex,:) = zeros(1,D); s(xindex,xindex)=1; f(xindex,1)=bc;
s(xindex+N*(M+1),:) = zeros(1,D);
s(xindex+N*(M+1),xindex+N*(M+1))=1;
f(xindex+N*(M+1),1)=bc;
end
for yindex=1:N-1
s(1+yindex*(M+1),:)=zeros(1,D);
s(1+yindex*(M+1),1+yindex*(M+1))=1;
f(1+yindex*(M+1),1)=bc;
s((1+yindex)*(M+1),:)=zeros(1,D);
s((1+yindex)*(M+1),(1+yindex)*(M+1))=1;
f((1+yindex)*(M+1),1)=bc;
end
q=s\f;
for yindex=1:N+1
for xindex=1:M+1
v(yindex,xindex) = q((M+1)*(yindex-1)+xindex);
end
end
[X,Y] = meshgrid(0:dx:L,0:dy:W);
[C,h] = contourf(X,Y,v);
clabel(C,h)
colormap cool