HW6, MAE 171. Spring 2005. UCI
Nasser Abbasi
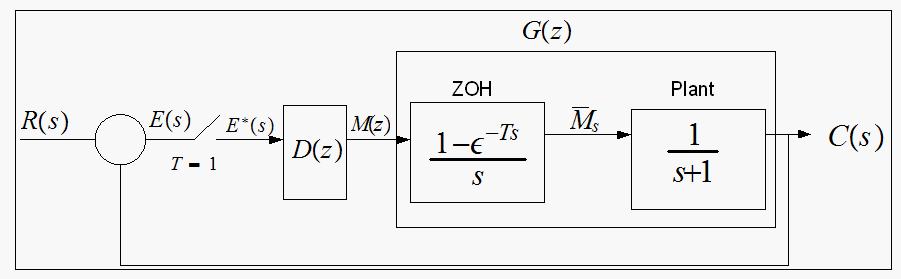
Consider system

The digital controller
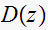 is described by difference equation
is described by difference equation
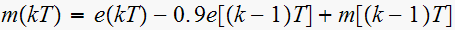
Find system type
Solution method: The system type is always taken relative to
the open loop transfer function. The type of the system is the number of poles
at
 for the case of a discrete system, or the number of poles at
for the case of a discrete system, or the number of poles at
 in
the case of the continuous system. So, determine the open loop tf and find its
poles.
in
the case of the continuous system. So, determine the open loop tf and find its
poles.
solution: First find
 ,
From the difference equation, take the Z transform, we obtain
,
From the difference equation, take the Z transform, we obtain
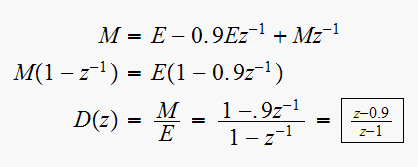
Hence the open loop transfer function is now
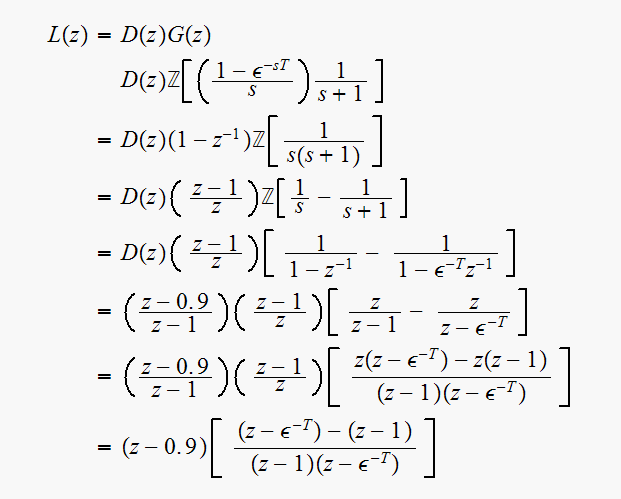
For
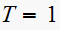
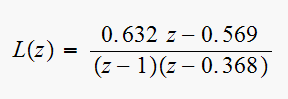
Hence we see that there is one pole at
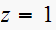 ,
hence the
,
hence the
Find the steady state response for a unit step input without finding
Solution method: Apply the final value theorem:
solution:
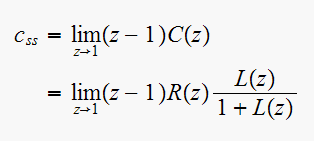
Since
 is a unit step, then
is a unit step, then
 then we get
then we get
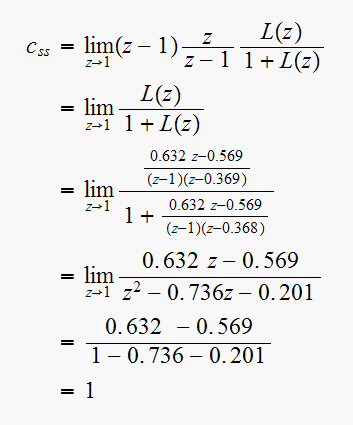
Another way to solve this is to find steady state error, and subtract that from the input. As follows
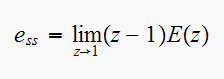
But
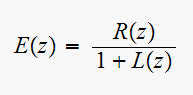
hence
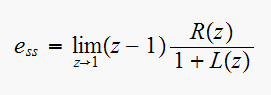
Since
 is a unit step, then
is a unit step, then
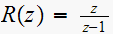 then we get
then we get
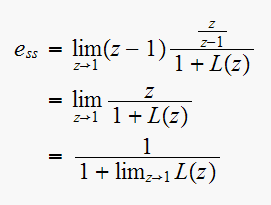
and using value for
 we found above, then we get
we found above, then we get
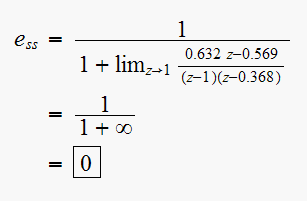
Since steady state error is zero, then steady state response must be equal to
input, which is
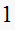 ,
hence
,
hence
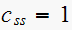
Find approximate time for system to reach steady state.
Solution method: Use relation
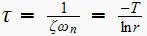 ,
where
,
where
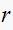 is the length of the dominant pole of the closed loop tf. Then set time to
reach steady state as
is the length of the dominant pole of the closed loop tf. Then set time to
reach steady state as
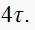
Solution: Time to reach steady state within
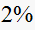 final value is
final value is
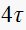 where
where
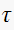 is the time constant of the closed loop transfer function. Hence need to
determine
is the time constant of the closed loop transfer function. Hence need to
determine
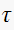 .
.
But
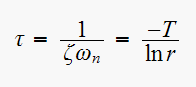
Where
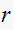 is the length of the dominant pole and
is the length of the dominant pole and
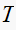 is the sampling time.
is the sampling time.
The closed loop transfer function is
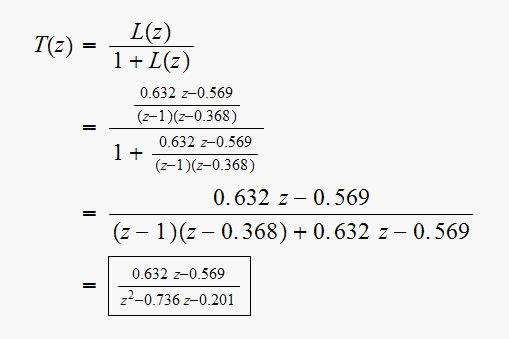 Zeros
of the denominator at
Zeros
of the denominator at
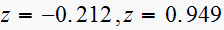
Then
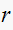 is
is
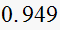
Hence
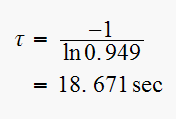
Hence it takes
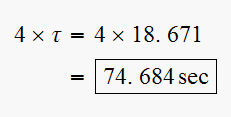
to reach steady state (using
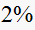 criterion)
criterion)
Find the unit step response for the system and verify parts (b) and (c)
solution method: Find response by evaluating
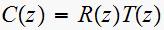
solution:
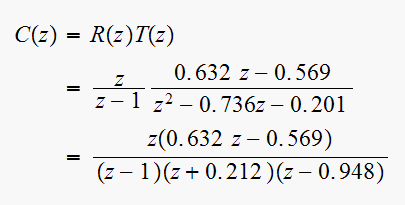
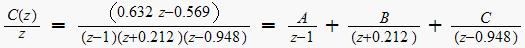
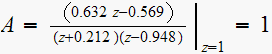
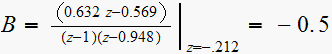
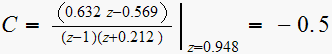
Hence
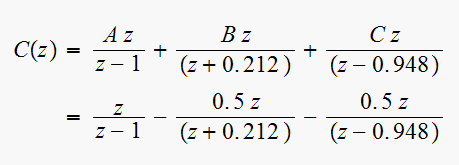
Hence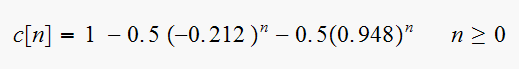
We see that as
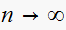 ,
,
![$c[n]\rightarrow 1$](graphics/hw6__58.gif) which verifies part(b)
which verifies part(b)
To verify part(c), set
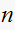 to be the closest integer to
to be the closest integer to
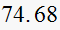 , which is the time to reach within
, which is the time to reach within
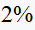 of final value. Since these are sample numbers, and the sample time
of final value. Since these are sample numbers, and the sample time
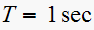 ,
then set
,
then set
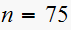 and find
and find
![$c[n]$](graphics/hw6__64.gif) for
for
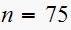 ,
we get
,
we get

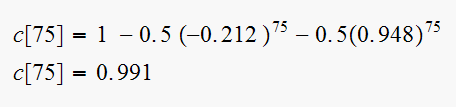
We see that at
![$c[75]$](graphics/hw6__68.gif) is within the
is within the
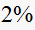 range (one percent on each side of the final value).
range (one percent on each side of the final value).
This verifies part(c)
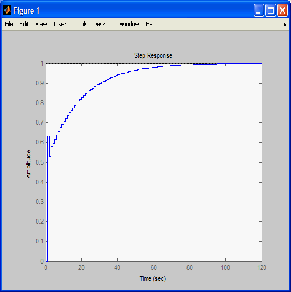
This is a MATLAB verification of response to unit step.
clear all; close all;
z=tf('z',1);
sys=(0.63212*z-0.56891)/(z^2-0.73576*z-0.20103)
step(sys)
Consider system
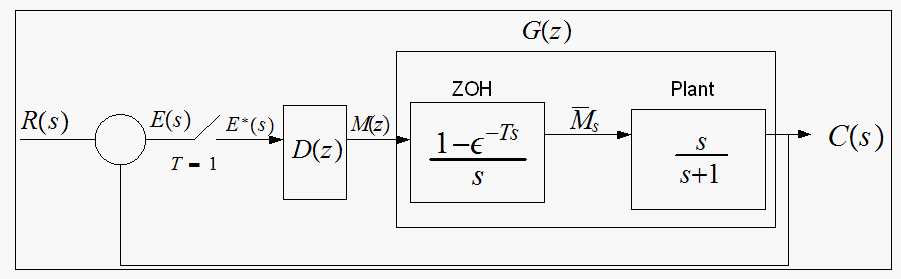
The digital controller
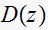 is described by difference equation
is described by difference equation
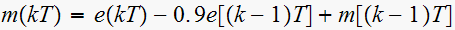
Find system type
Solution method: The system type is always taken relative to
the open loop transfer function. The type of the system is the number of poles
at
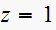 for the case of a discrete system, or the number of poles at
for the case of a discrete system, or the number of poles at
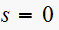 in
the case of the continuous system. So, determine the open loop tf and find its
poles.
in
the case of the continuous system. So, determine the open loop tf and find its
poles.
solution:
From problem 6-15,
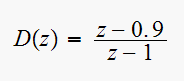
Hence the open loop transfer function is now
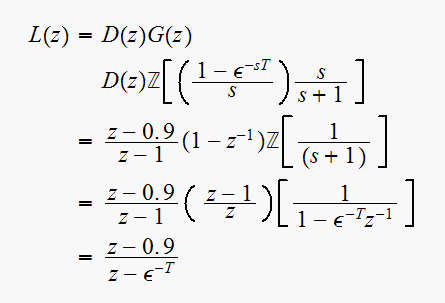
For
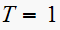
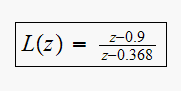
Hence we see that now there are no pole at
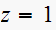 ,
hence the
,
hence the
Find the steady state response for a unit step input without finding
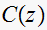
Apply the final value theorem:
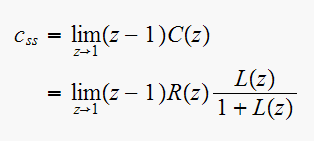
Since
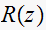 is a unit step, then
is a unit step, then
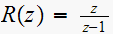 then we get
then we get
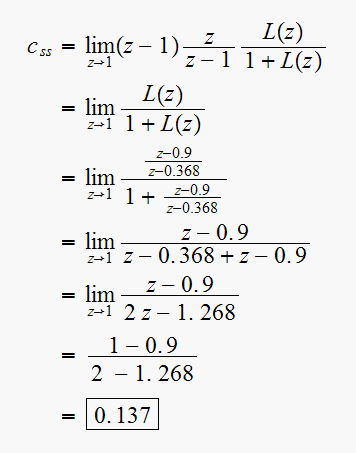
Find approximate time for system to reach steady state.
Time to reach steady state within
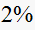 final value is
final value is
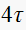 where
where
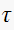 is the time constant of the closed loop transfer function. Hence need to
determine
is the time constant of the closed loop transfer function. Hence need to
determine
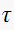 .
.
But
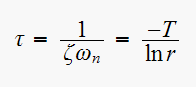
Where
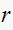 is the length of the dominant pole and
is the length of the dominant pole and
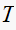 is the sampling time.
is the sampling time.
The closed loop transfer function is
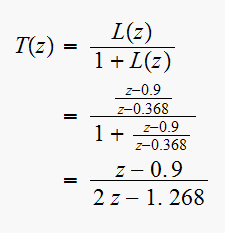
Zeros of the denominator at
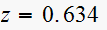
Then
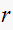 is
is
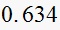
Hence
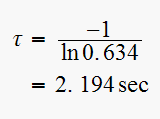
Hence it takes
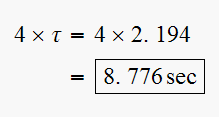
to reach steady state (using
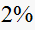 criterion)
criterion)
Find the unit step response for the system and verify parts (b) and (c)
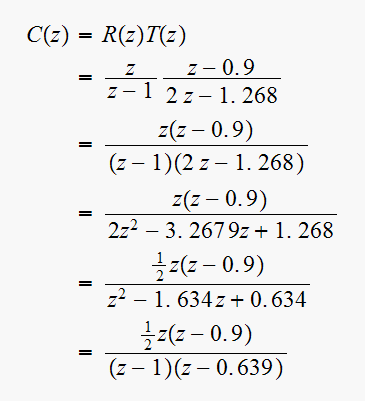
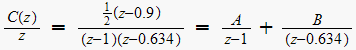
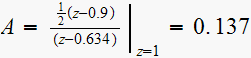
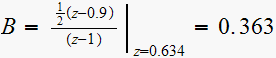
Hence
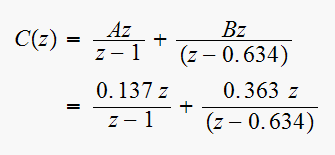
Hence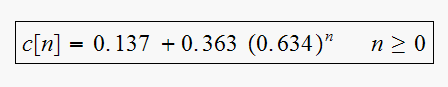
We see
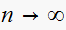 ,
,
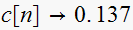
To verify part(c), set
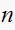 to be the closest integer to
to be the closest integer to
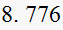 , which is the time to reach within
, which is the time to reach within
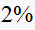 of final value. Since these are sample numbers, and the sample time
of final value. Since these are sample numbers, and the sample time
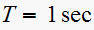 ,
then set
,
then set
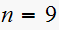 and find
and find
![$c[n]$](graphics/hw6__118.gif) for
for
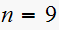 ,
we get
,
we get

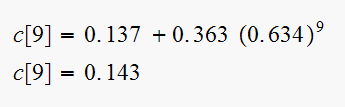 Since
the final value of
Since
the final value of
![$c[n]$](graphics/hw6__122.gif) is
is
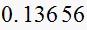 ,
then this error is
,
then this error is
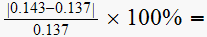
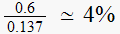 .
This is good enough approximation to final value, so this verifies part(c).
.
This is good enough approximation to final value, so this verifies part(c).
Given the following characteristic equations
iii)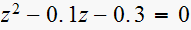 vi)
vi)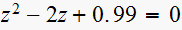 vii)
vii)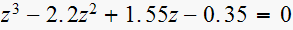 viii)
viii)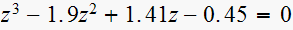
In these problems, the equation is expressed in form
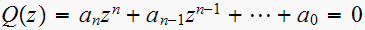 ,
,
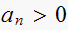
Use Jury test to determine stability of each system
iii)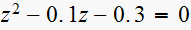
test1: is
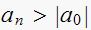 ,
i.e. is
,
i.e. is
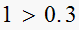 ,
YES, test pass.
,
YES, test pass.
test2: is
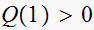 ,
i.e. is
,
i.e. is
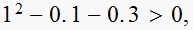 YES, test pass.
YES, test pass.
test3:
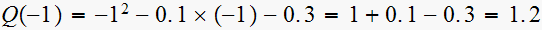 ,
hence
,
hence
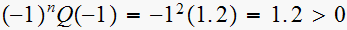 .
hence
.
hence
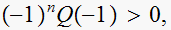 YES,
test pass.
YES,
test pass.
Since second order system, no need to construct Jury table.
Hence
vi)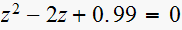
test1: is
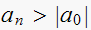 ,
i.e. is
,
i.e. is
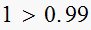 ,
YES, test pass.
,
YES, test pass.
test2: is
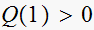 ,
i.e. is
,
i.e. is
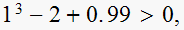 NO, test pass.
NO, test pass.
Hence
vii)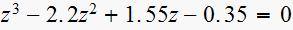
test1: is
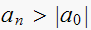 ,
i.e. is
,
i.e. is
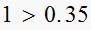 ,
YES, test pass.
,
YES, test pass.
test2: is
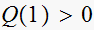 ,
i.e. is
,
i.e. is
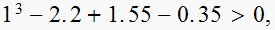 NO, test fails
NO, test fails
Hence
viii)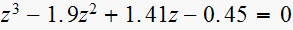
test1: is
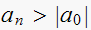 ,
i.e. is
,
i.e. is
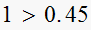 ,
YES, test pass.
,
YES, test pass.
test2: is
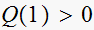 ,
i.e. is
,
i.e. is
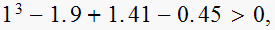 is
is
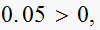 YES,
test pass.
YES,
test pass.
test3:
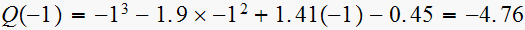 ,
hence
,
hence
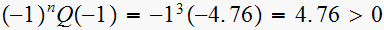 .
hence
.
hence
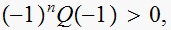 YES,
test pass.
YES,
test pass.
construct jury table
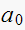 |
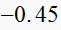 |
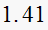 |
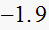 |
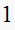 |
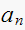 |
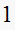 |
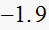 |
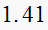 |
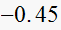 |
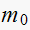 |
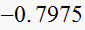 |
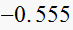 |
is
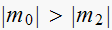 ,
is
,
is
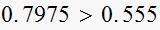 ,
YES. test pass.
,
YES. test pass.
Hence
List the natural response terms for each of the systems.
Solution method: roots of characteristic equation that appear
at
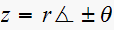 result in natural response terms of the form
result in natural response terms of the form
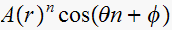
solution:
iii)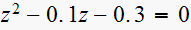
zeros are
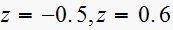
Hence for the first pole, we have
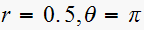 ,
hence this pole contributes a term of the form
,
hence this pole contributes a term of the form
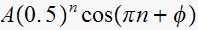
For the first pole, we have
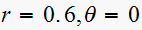 ,
hence this pole contributes a term of the form
,
hence this pole contributes a term of the form
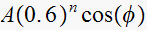
So if we let
![$y[n]$](graphics/hw6__182.gif) be the natural response, we can write
be the natural response, we can write
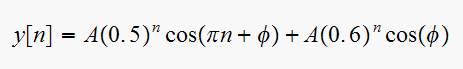
vi)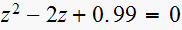
zeros are
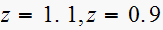
Hence for the first pole, we have
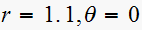 ,
hence this pole contributes a term of the form
,
hence this pole contributes a term of the form
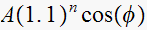
For the first pole, we have
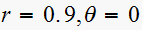 ,
hence this pole contributes a term of the form
,
hence this pole contributes a term of the form
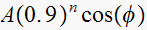
So if we let
![$y[n]$](graphics/hw6__190.gif) be the natural response, we can write
be the natural response, we can write
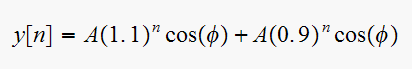
vii)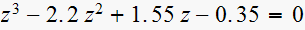
zeros are
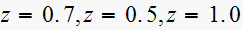
First pole contributes a term of the form
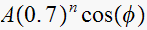
Second pole contributes a term of the form
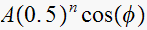
Third pole contributes a term of the form
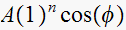
So if we let
![$y[n]$](graphics/hw6__197.gif) be the natural response, we can write
be the natural response, we can write
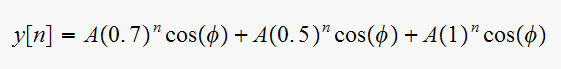
viii)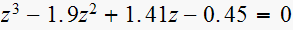
zeros are
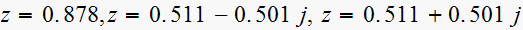
First pole
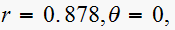 so it contributes a term of the form
so it contributes a term of the form
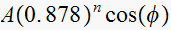
Second pole
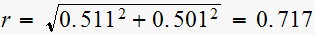 ,
,
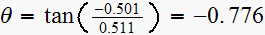
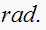 So this pole contributes a term of the form
So this pole contributes a term of the form
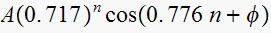
Third pole contributes the same term as above.
So if we let
![$y[n]$](graphics/hw6__207.gif) be the natural response, we can write
be the natural response, we can write
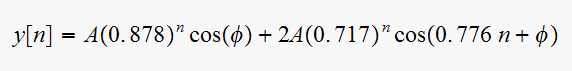
For those systems in part(a) that are found to be either unstable or marginally stable, list the natural response terms in part(b) that yield these results.
From part(a), these are the systems found to be unstable
vi)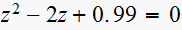
vii)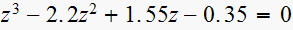
For system vi, the natural response term that causes the instability is as shown below
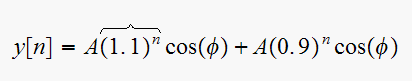
This terms comes from the pole at
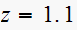
For system vii, the natural response term that causes the
marginal instability is as shown below
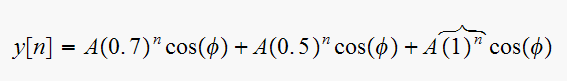
This term comes from the pole at
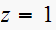
Consider the system shown below. Let the digital controller be
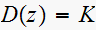 .
.
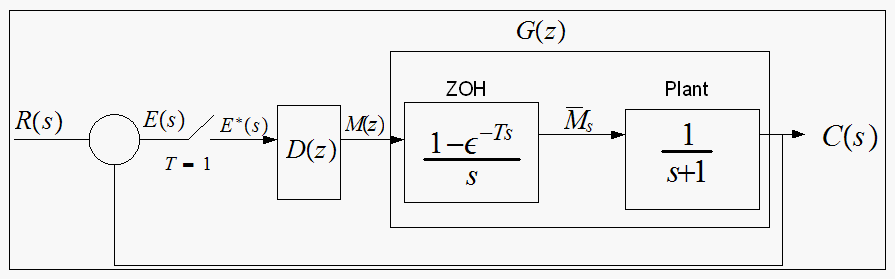
write the closed loop system characteristic equation.
The open loop transfer function is now
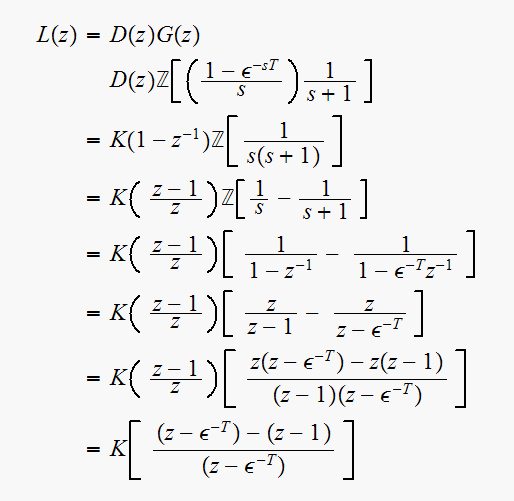
For
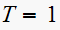
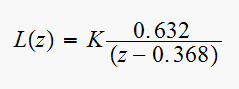
The closed loop transfer function is
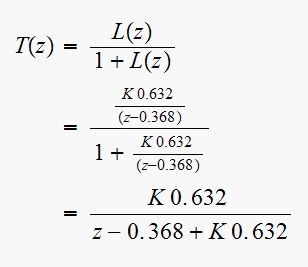
Hence closed loop characteristic equation is
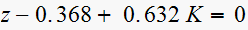
determine the range of
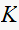 for which the closed loop system is stable
for which the closed loop system is stable
Here
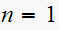 ,
and
,
and
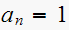 ,
,
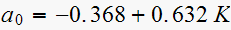
For stability need
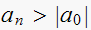 ,
hence
,
hence
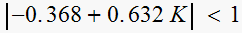 ,
hence
,
hence
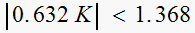 ,
hence
,
hence
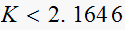
The second test
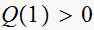 yields
yields
Third test
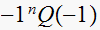 yields
yields
Hence
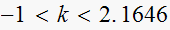
Supposed that
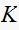 is set to the lower limit found in part(b), find the natural response term and
illustrate the marginal instability
is set to the lower limit found in part(b), find the natural response term and
illustrate the marginal instability

set
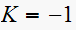
Hence the closed loop system characteristic equation is
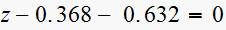 or
or
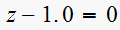
Hence we have a pole at
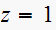 which maps to the origin in the S-plane. A pole at
which maps to the origin in the S-plane. A pole at
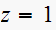 means the system is marginally unstable. This pole will contribute a term of
the form
means the system is marginally unstable. This pole will contribute a term of
the form
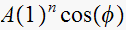 to the natural solution. Since there is only one term here, we see that the
natural response is simply
to the natural solution. Since there is only one term here, we see that the
natural response is simply
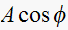 ,
which will not decay, hence the system will continue to oscillate as it is
marginally unstable.
,
which will not decay, hence the system will continue to oscillate as it is
marginally unstable.
Repeat part(c) for the upper limit of
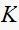
set
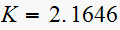
Hence the closed loop system characteristic equation is
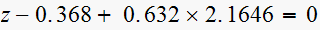 or
or
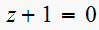
Hence we have a pole at
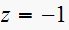 .
This pole will contribute a term of the form
.
This pole will contribute a term of the form
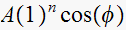 to the natural solution. Since there is only one term here, we see that the
natural response is simply
to the natural solution. Since there is only one term here, we see that the
natural response is simply
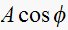 ,
which will not decay, hence the system will continue to oscillate as it is
marginally unstable.
,
which will not decay, hence the system will continue to oscillate as it is
marginally unstable.
Verify the result of this problem by digital computation.
Using Matlab it is shown that the step response for values just outside the
range of
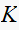 will result in an unstable system and for values just inside the range, the
step response is stable.
will result in an unstable system and for values just inside the range, the
step response is stable.
This is the output.
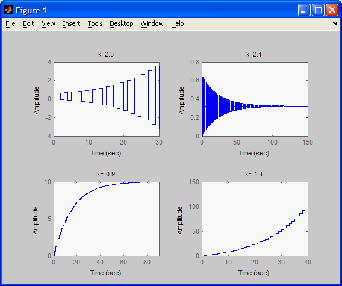
MATLAB code:
function nma_test_prob_7_6
close all; clear all;
n=1;
subplot(2,2,n);
do(2.3);
n=n+1;
subplot(2,2,n);
do(2.1);
n=n+1;
subplot(2,2,n);
do(-0.9);
n=n+1;
subplot(2,2,n);
do(-1.1);
function do(k)
z=tf('z');
sys=0.632/(z-0.368+0.632*k);
step(sys);
title(sprintf('k=%2.1f',k));