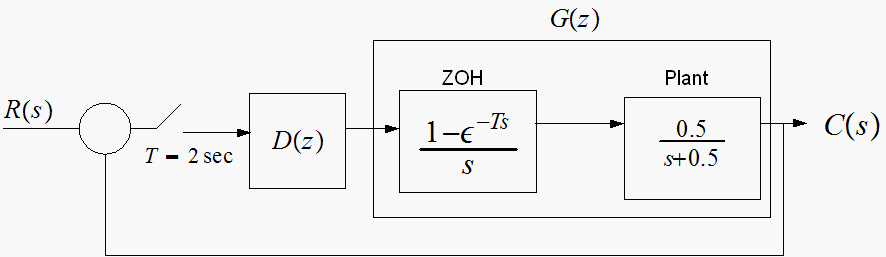
HW5, MAE 171. Spring 2005. UCI
Nasser Abbasi

Calculate and plot the unit-step response at the sampling instances for the
case when
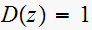
First find the open loop
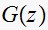
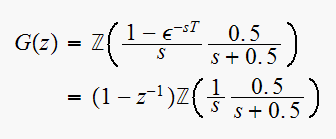
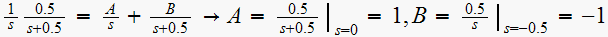
Hence
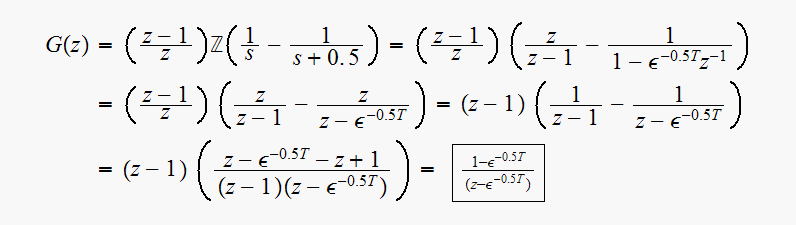
Hence the closed loop transfer function is, noting that
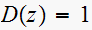
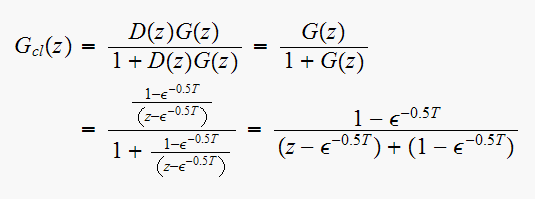
For
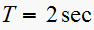 we get from (1)
we get from (1)
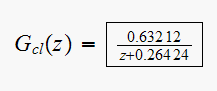
Now since the input is a unit step, then
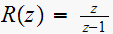
Hence the output
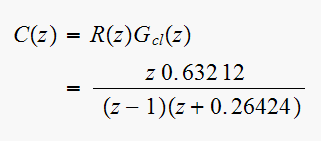
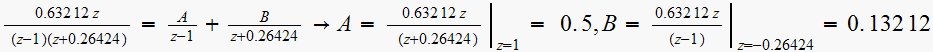
Hence
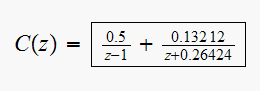
From tables, the inverse Z transform of
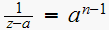
 for
for
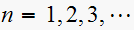
Hence
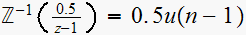
And
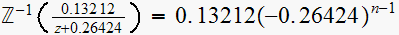
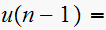

Hence The inverse Z transform of
 is
is
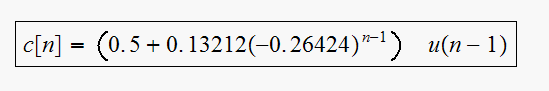
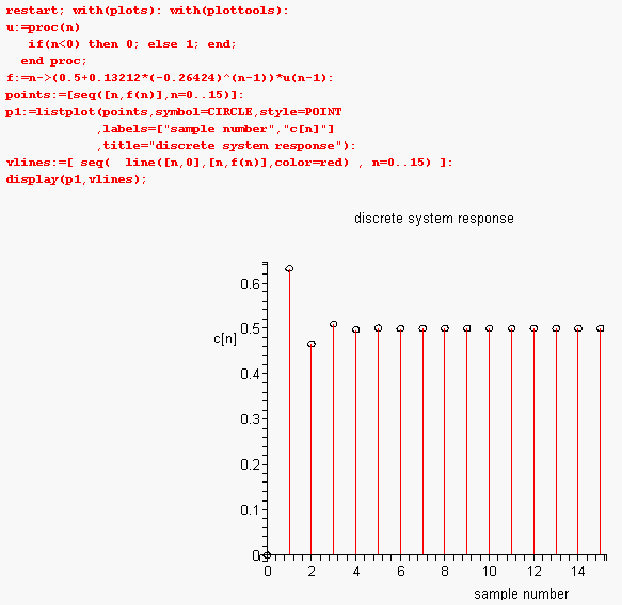
This is a plot of
![$c[n]$](graphics/hw5__28.gif)
Calculate the system unit step response for the analog system. Plot the response on the same graph as the result of (a).
The closed loop transfer function is
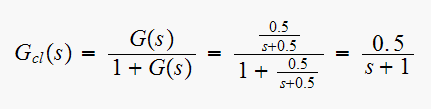
Hence
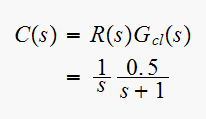
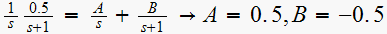
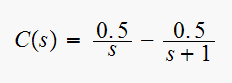
Hence
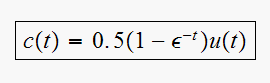
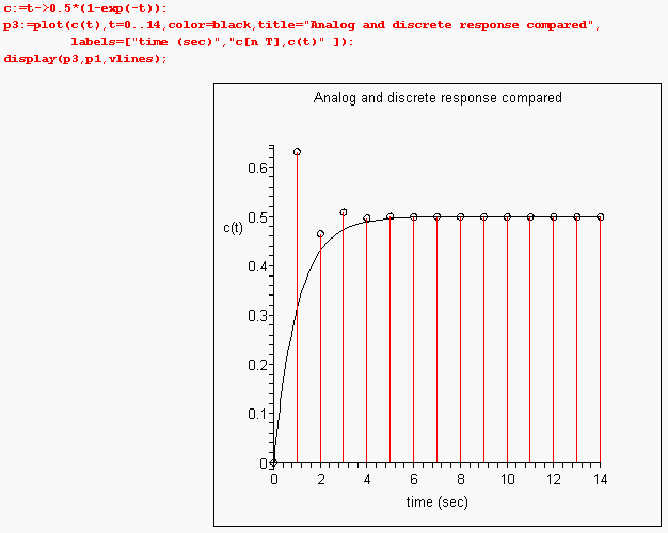
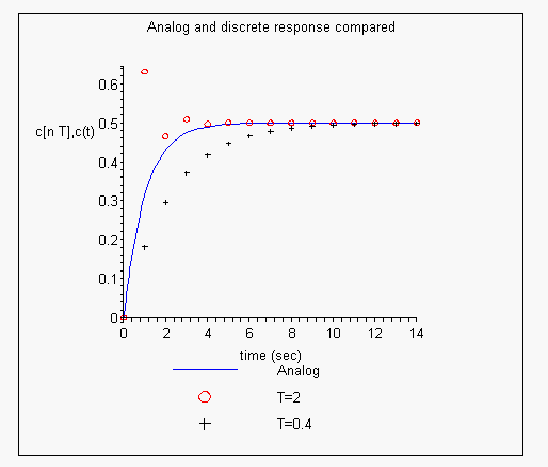
Here is a graph which shows the analog and discrete responses
Let
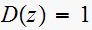 and
and
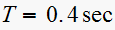 .
Calculate the unit step response and plot these on the same plot
.
Calculate the unit step response and plot these on the same plot
From equation (1) in part(a), we have
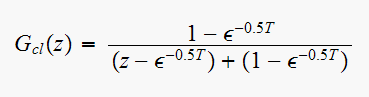
for
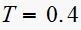
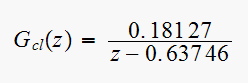
Now since the input is a unit step, then
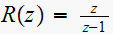
Hence the output
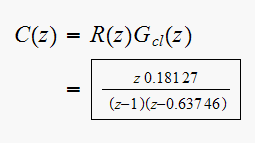
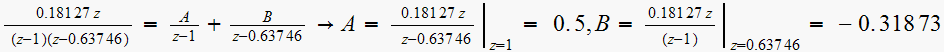
Hence
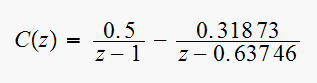
From tables, the inverse Z transform of
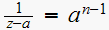
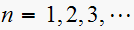
Hence
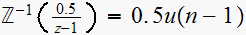
And
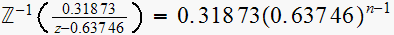
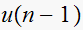
Hence The inverse Z transform of
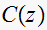 is
is

The following is the plot comparing discrete system response for
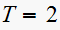 and
and
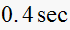 with the pure analog system.
with the pure analog system.
Notice the effect of changing
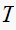 on the discrete response. For larger
on the discrete response. For larger
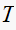 the system had a larger overshoot and was less damped. As sampling rate
increased the response exhibited over damping.
the system had a larger overshoot and was less damped. As sampling rate
increased the response exhibited over damping.
Consider the sampeld-data systems with the following char. equation
(1)
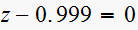
(2)
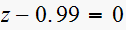
(3)
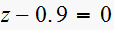
(4)
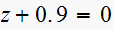
(5)
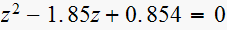
(6)
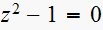
(7)
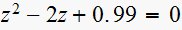
(8)
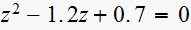
This table summarizes the results.
| system | 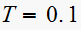 |
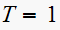 |
|||||||
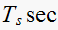 |
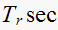 |
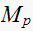 |
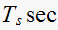 |
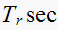 |
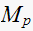 |
||||
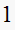 |
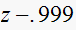 |
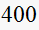 |
N/A | N/A | 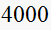 |
N/A | N/A | ||
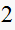 |
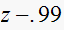 |
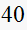 |
N/A | N/A | 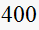 |
N/A | N/A | ||
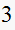 |
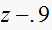 |
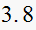 |
N/A | N/A | 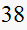 |
N/A | N/A | ||
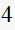 |
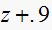 |
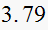 |
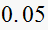 |
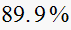 |
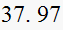 |
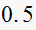 |
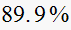 |
||
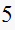 |
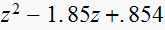 |
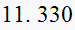 |
N/A | N/A | 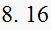 |
N/A | N/A | ||
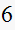 |
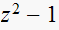 |
N/A | N/A | N/A | N/A | N/A | N/A | ||
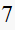 |
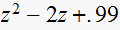 |
N/A | N/A | N/A | N/A | N/A | N/A | ||
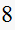 |
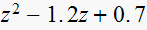 |
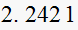 |
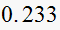 |
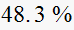 |
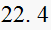 |
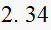 |
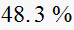 |
From the table above we observe that the
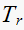 (rise time) and
(rise time) and
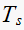 (settling time) varies with
(settling time) varies with
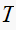 only. While
only. While
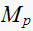 is not affected.
is not affected.
As
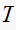 becomes larger (slower sampling), the response will take longer to rise and to
settle. The ratio of the change in
becomes larger (slower sampling), the response will take longer to rise and to
settle. The ratio of the change in
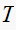 is the same ratio by which the response will take longer to settle for these
systems. To classify the responses, this table and the plots show the
classification. This Next plot is the transient response characteristics of
the systems for
is the same ratio by which the response will take longer to settle for these
systems. To classify the responses, this table and the plots show the
classification. This Next plot is the transient response characteristics of
the systems for
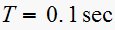
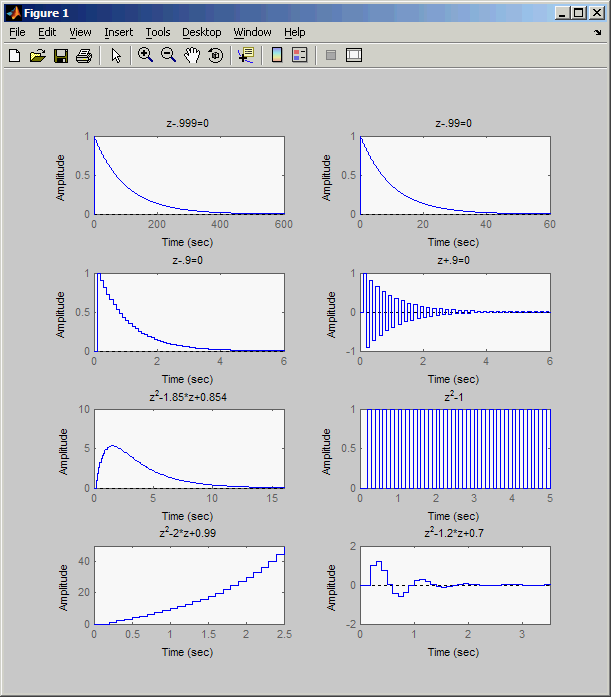
| system | 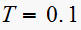 |
||
 |
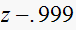 |
stable | |
 |
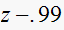 |
stable | |
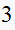 |
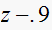 |
stable | |
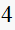 |
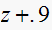 |
stable,exponential damped sinusoidal | |
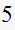 |
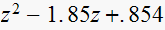 |
stable,damped | |
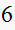 |
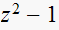 |
marginal unstable. | |
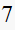 |
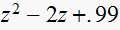 |
unstable, exponential | |
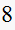 |
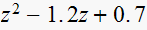 |
stable, exponential damped sinusoidal |
What can you determine about the system natural response characteristic for
each system for
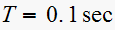 ?
?
For second order system we can determine the transient response characteristic as follows.
From the location of the discrete transfer function poles, we determine
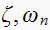 using the three equations below. And in turn from
using the three equations below. And in turn from
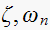 we can determine, using the simplified equations, the rise time
we can determine, using the simplified equations, the rise time
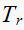 ,
the maximum overshoot
,
the maximum overshoot
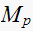 and the settling time
and the settling time
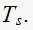 In addition we can find the time constant
In addition we can find the time constant
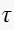 from knowing
from knowing
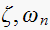
Let a Z system pole be expressed as
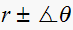 ,
then these are the equations to use: (see book page 216 for the derivation)
,
then these are the equations to use: (see book page 216 for the derivation)
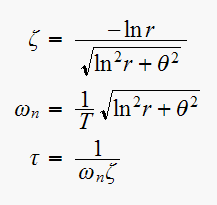
We can now determine
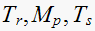 for the system response to a unit step.
for the system response to a unit step.
For
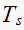 use
use
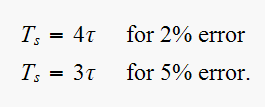
For
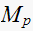 (since this is a unit step response, hence the final value is 1), we get
(since this is a unit step response, hence the final value is 1), we get
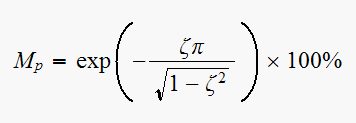
For
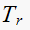 use
use
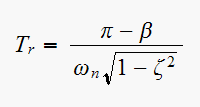
where
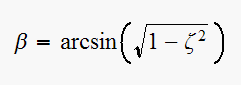
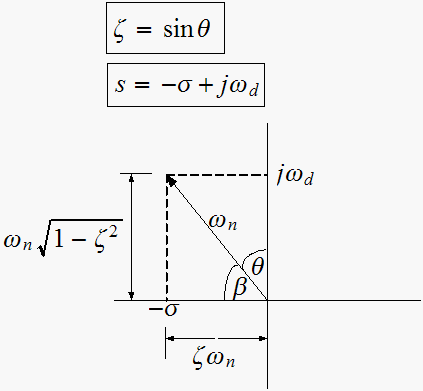
For a first order discrete system, the response will not exhibit oscillations
if the root is positive. So for a first order system with positive root we can
only say something about
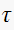 ,
the time constant (which is the time required for response to reach
,
the time constant (which is the time required for response to reach
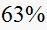 of its final value.)
of its final value.)
Assume root of Z system is at
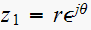 but since this is a real positive root, then
but since this is a real positive root, then
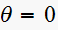 ,
and
,
and
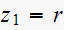 and since
and since
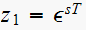 ,
we get that
,
we get that
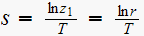 where
where
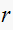 here is the magnitude of
here is the magnitude of
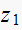
Hence from
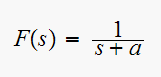
We see that
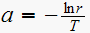 hence since
hence since
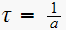 then we get
then we get
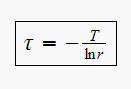
Now, For a first order discrete system, the response will exhibit oscillations if the root is negative.
Assume root of Z system is at
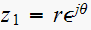 but since this is a real negative root, then
but since this is a real negative root, then
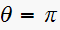 ,
and
,
and
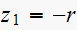 and since
and since
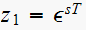 ,
we get that
,
we get that
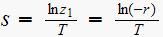 where
where
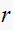 here is the magnitude of
here is the magnitude of
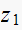 and hence since we are taking the natural log of a negative value, then
and hence since we are taking the natural log of a negative value, then
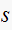 is a complex value say
is a complex value say
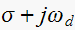 ,
from which we find
,
from which we find
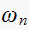 and
and
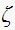 and then we can find the rest of the transient response properties since
and then we can find the rest of the transient response properties since
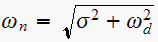 and
we find
and
we find
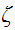 from
from
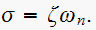
Now we can start to solve the problems
(1)
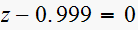
Since is a first order system. root
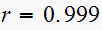 hence from
hence from
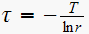 we get
we get
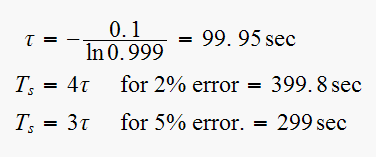
(2)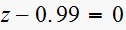
Since is a first order system. root
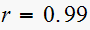 hence from
hence from
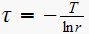 we get
we get
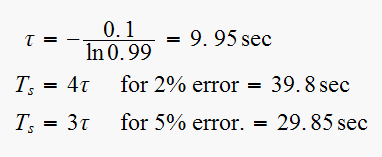
Notice that for a small change in the location of the root
(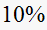 change), the system now responds
change), the system now responds
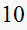 times as fast.
times as fast.
(3)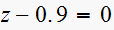
Since is a first order system. root
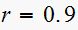 hence from
hence from
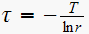 we get
we get
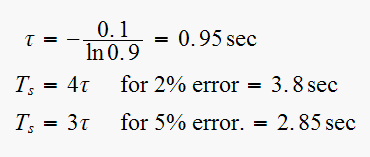
Notice that for a small change in the location of the root
(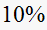 change), the system now responds
change), the system now responds
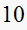 times as fast.
times as fast.
(4)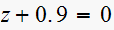
Since is a first order system. since root
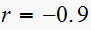 hence transient response will oscillate.
hence transient response will oscillate.
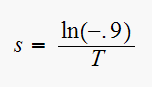
To evaluate
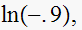 since
since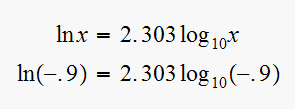
Let
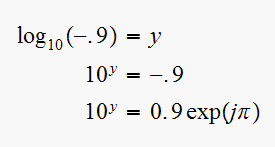
Hence
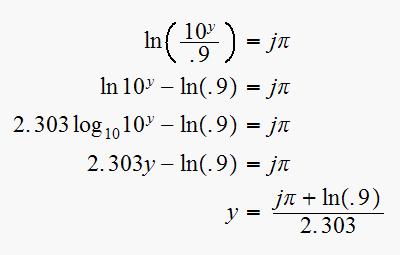
From (1) we
get
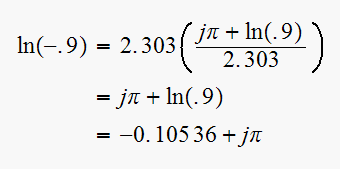
Hence
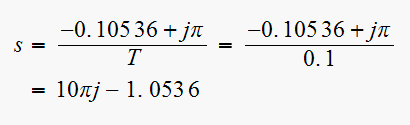
Hence
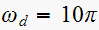 and
and
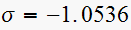
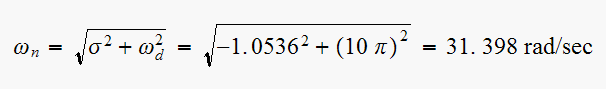
and
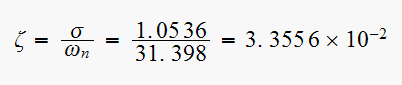
Hence now we can obtain the transient response characteristics.
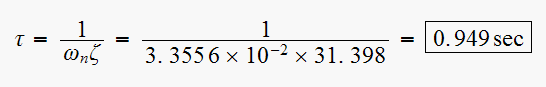
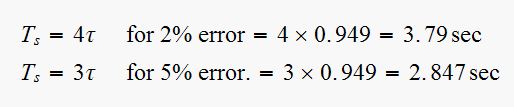
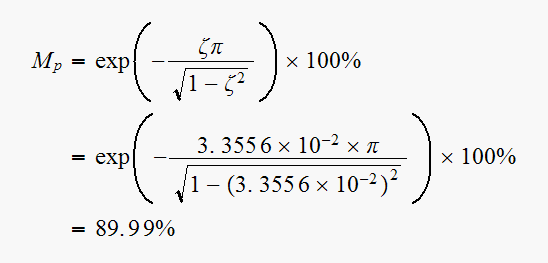
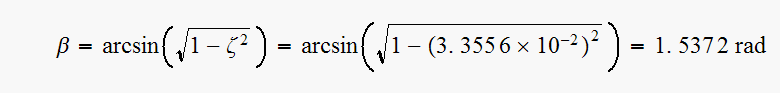
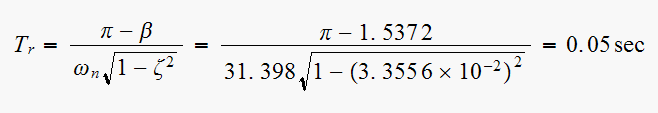
(5)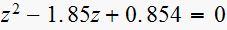 ,
Solution is:
,
Solution is:
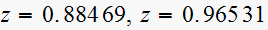
Since there are no complex poles, and both poles positive, then system will
not oscillate even though it is a second order system. Hence we know that
 and
and
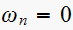 and
and
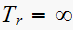 in this case since we will use
in this case since we will use
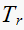 here as the time to go from
here as the time to go from
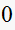 to
to
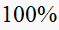 of the final value.
of the final value.
using
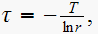 there
are 2 time constants since there are 2 roots, we get
there
are 2 time constants since there are 2 roots, we get
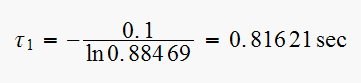
and
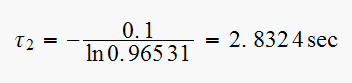
We pick the larger time constant since that is associated with the dominant pole.
hence
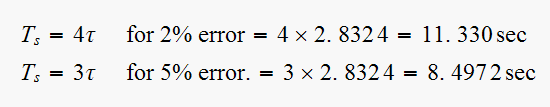
(6)
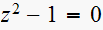
poles are at
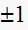
This is a marginally unstable system. For an input of
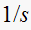 ,
we see that the pole of the input equals the pole of the system at
,
we see that the pole of the input equals the pole of the system at
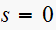 ,
hence resonance will occur. So not applicable to determine the transient
characteristic.
,
hence resonance will occur. So not applicable to determine the transient
characteristic.
(7)
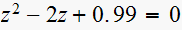 ,
Solution is:
,
Solution is:
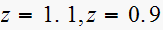
We have a pole outside the unit circle. Hence this is unstable system. So not applicable to determine the transient characteristic.
(8)
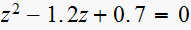 ,
Solution is:
,
Solution is:
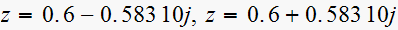
Here the pole is
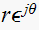 where
where
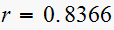 and
and
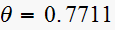 rad
rad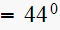

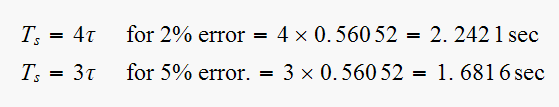
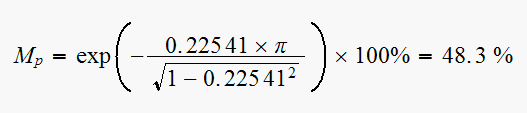
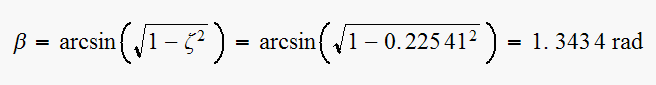
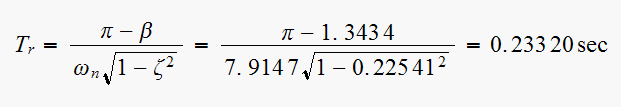
Redo part(a) for
(1)
Since is a first order system. root
 hence from
hence from
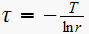 we get
we get
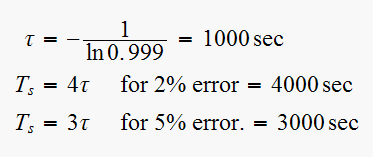
(2)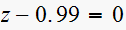
Since is a first order system. root
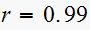 hence from
hence from
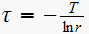 we get
we get
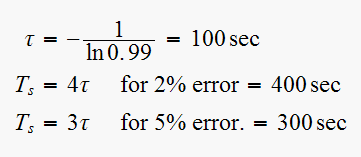
(3)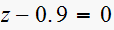
Since is a first order system. root
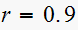 hence from
hence from
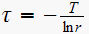 we get
we get
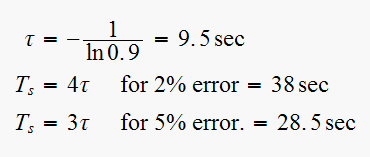
(4)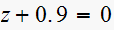
As from part (a), we get
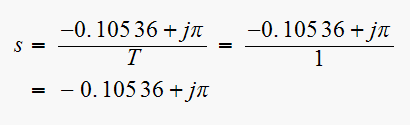
Hence
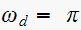 and
and
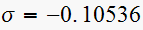
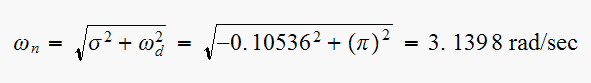
and
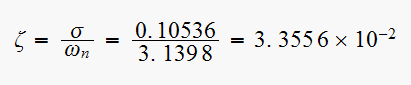
Hence now we can obtain the transient response characteristics.
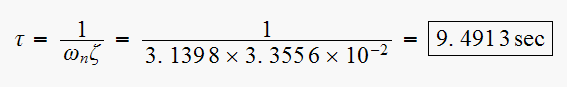
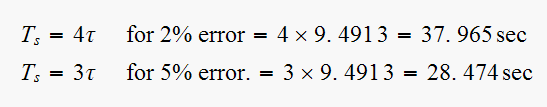
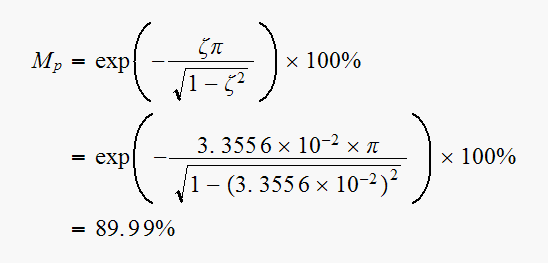
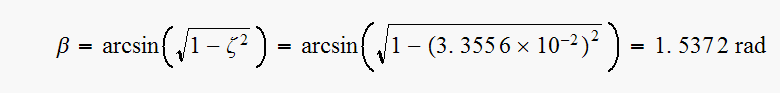
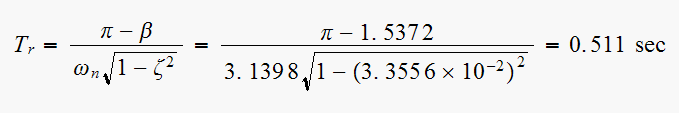
(5)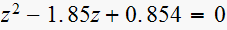 ,
Solution is:
,
Solution is:
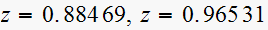
using
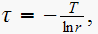 there
are 2 time constants since there are 2 roots, we get
there
are 2 time constants since there are 2 roots, we get
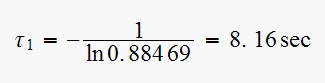
and
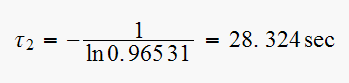
We pick the larger time constant since that is associated with the dominant pole.
hence
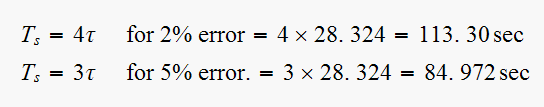
(6)
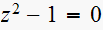
poles are at
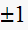
This is a marginally unstable system. For an input of
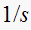 ,
we see that the pole of the input equals the pole of the system at
,
we see that the pole of the input equals the pole of the system at
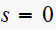 ,
hence resonance will occur. So not applicable to determine the transient
characteristic.
,
hence resonance will occur. So not applicable to determine the transient
characteristic.
(7)
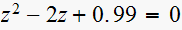 ,
Solution is:
,
Solution is:
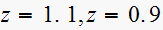
We have a pole outside the unit circle. Hence this is unstable system. So not applicable to determine the transient characteristic.
(8)
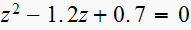 ,
Solution is:
,
Solution is:
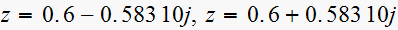
Here the pole is
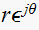 where
where
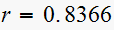 and
and
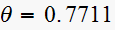 rad
rad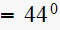
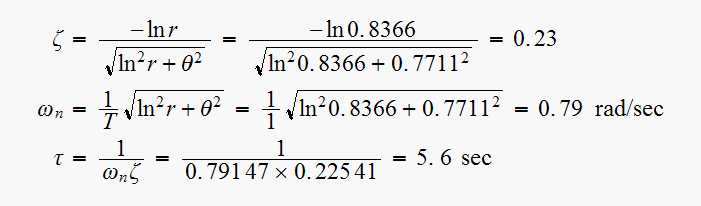
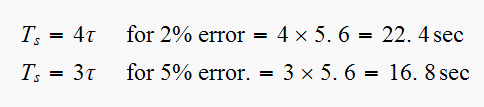
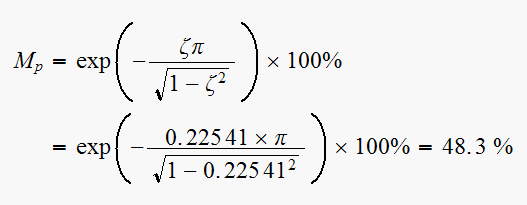

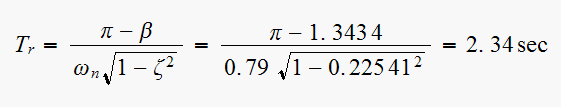
From the table above we observe that the
 (rise time) and
(rise time) and
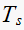 (settling time) varies with
(settling time) varies with
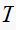 only. While
only. While
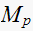 is not affected.
is not affected.
The following system has parameters
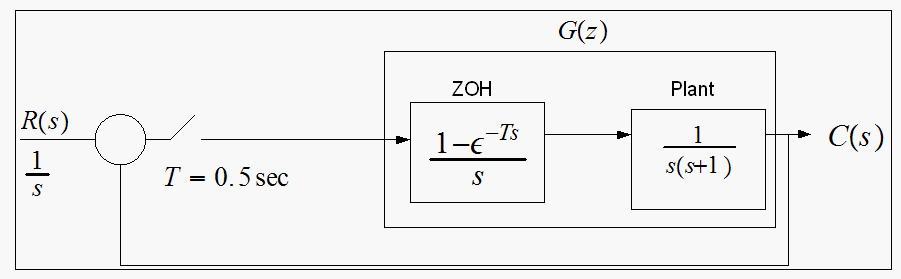
Find
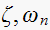 and
and
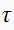 for the sample period
for the sample period
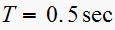
Find open loop
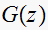 then the closed loop
then the closed loop
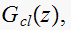 then find the zeros of the characteristic equation, and from these find
then find the zeros of the characteristic equation, and from these find
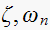 and
and
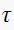 using the relations
using the relations
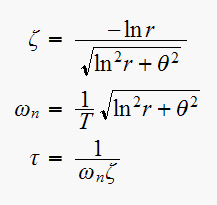
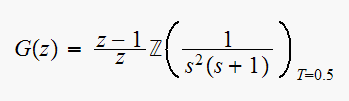
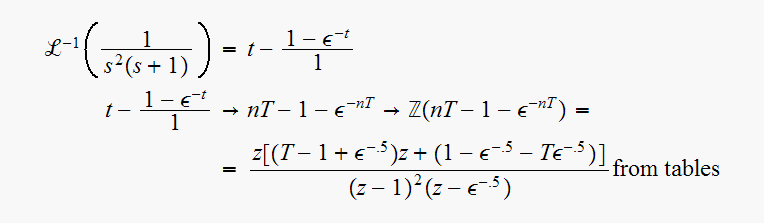
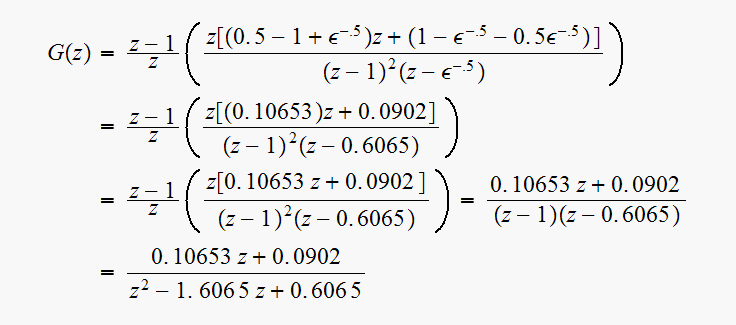
So
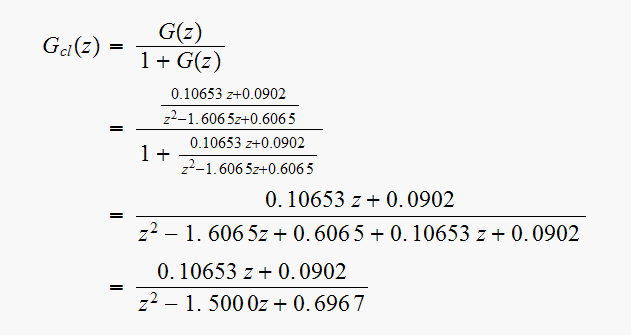
Characteristic equation
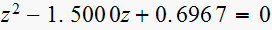 ,
Solution is:
,
Solution is:
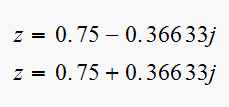
Hence
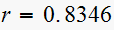 and
and
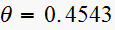 rad
rad
Hence
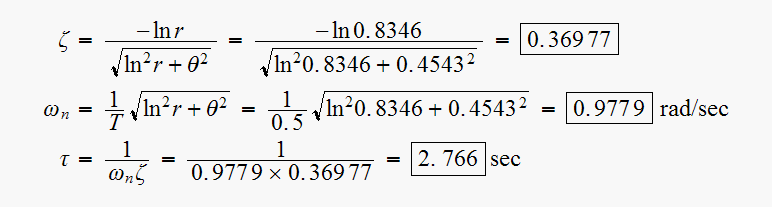
redo part (a) with
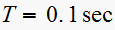
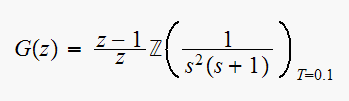
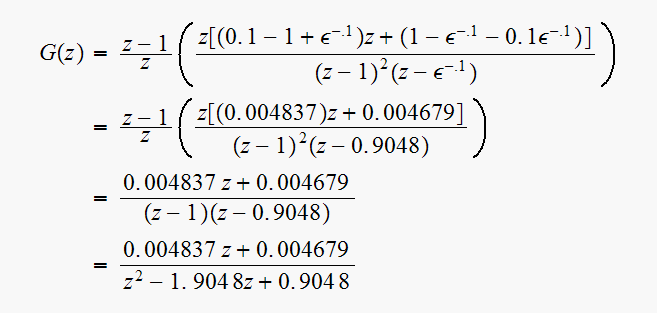
So

Characteristic equation
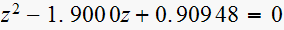 ,
Solution is:
,
Solution is:
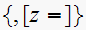 ,
Solution is:
,
Solution is:

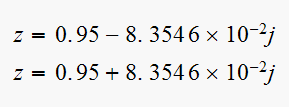
Hence
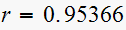 and
and
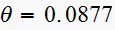 rad
rad
Hence

repeat part(a) for analog system.
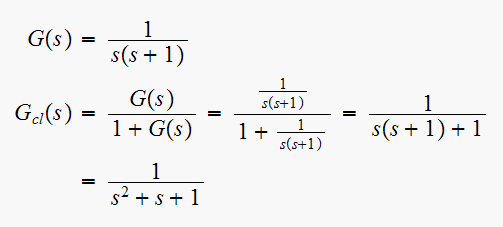
Hence
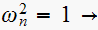
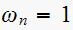
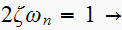
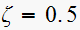
Hence
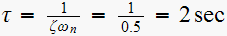
Give table listing the three parameters as function of sampling frequency
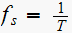 .
State the result of decreasing the sampling frequency on the parameters.
.
State the result of decreasing the sampling frequency on the parameters.
Solution summary table
| T sec | 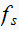 |
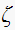 |
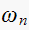 rad/sec
rad/sec |
 |
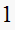 |
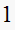 |
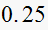 |
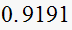 |
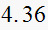 |
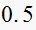 |
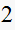 |
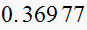 |
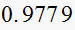 |
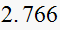 |
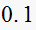 |
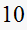 |
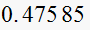 |
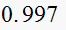 |
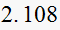 |
| analog | 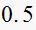 |
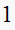 |
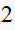 |
We see as the sampling frequency
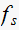 becomes smaller, then the damping ratio decreases, this means the response
will become more oscillatory in the transient stage with larger overshoot.
becomes smaller, then the damping ratio decreases, this means the response
will become more oscillatory in the transient stage with larger overshoot.
