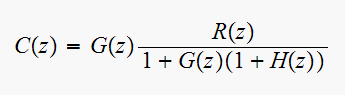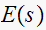 and
and
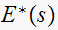 in the s-plane. Let
in the s-plane. Let
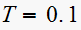
HW4, MAE 171. Spring 2005. UCI
Nasser Abbasi
Find the Z transform of the following functions, using the z-transform tables.
Compare the pole-zero locations of
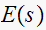 and
and
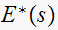 in the s-plane. Let
in the s-plane. Let
Note: The problem did not mention this, but since we must have same number of zeros and poles for a transfer function (this is when we consider both finite and non-finite zeros), hence, in this problem, I will find all such zeros.
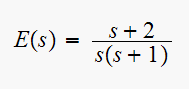
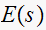 at
at
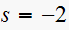 ,
non-finite zeros at
,
non-finite zeros at
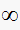 ,
and , poles are at
,
and , poles are at
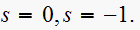
From problem 3-4 (which we did in HW3),
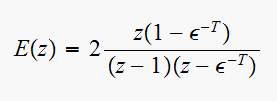
For
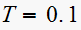 ,
,
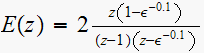
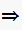
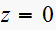 ,
non-finite zero at
,
non-finite zero at
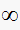 ,
poles at
,
poles at
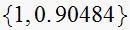
Now to find poles/zeros of
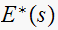 .
.
We can solve this directly from the expression for
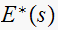 ,
but an easier method is as follows. We know the poles of
,
but an easier method is as follows. We know the poles of
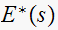 to be located at distances of
to be located at distances of
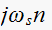 From
the poles of
From
the poles of
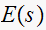 for
for
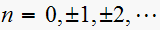 , So by knowing the poles of
, So by knowing the poles of
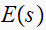 we find the poles of
we find the poles of
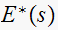 .
.
However, for the zeros of
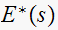 ,
there is no such correlation, but the zeros of
,
there is no such correlation, but the zeros of
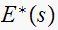 are still periodic of period
are still periodic of period
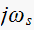
Since we know the poles of
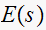 to be located at
to be located at
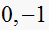 ,
then we can find the poles of
,
then we can find the poles of
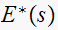 that are periodic with pole
that are periodic with pole
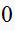 to be at
to be at
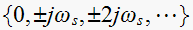 and the poles of
and the poles of
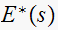 that are periodic with pole at
that are periodic with pole at
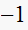 to be at
to be at
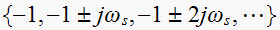
Since
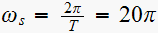 rad/sec, hence the poles of
rad/sec, hence the poles of
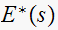 are at
are at
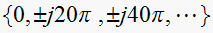
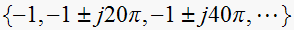
Now to find the zeros of
 ,
since
,
since
 ,
then
,
then

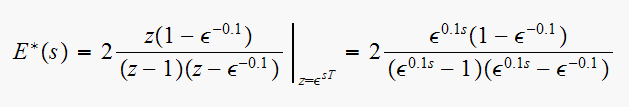
Hence a zero of
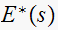 is when
is when
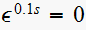 or when
or when
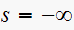 .
There is also a zero when
.
There is also a zero when
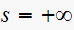 ,
since that will make the denominator blow up. Since number of zeros must match
the number of poles, we can generate the rest of the zeros from periodic
repetition (but zeros are already at
,
since that will make the denominator blow up. Since number of zeros must match
the number of poles, we can generate the rest of the zeros from periodic
repetition (but zeros are already at
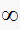
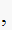 so the rest of the zeros are all at
so the rest of the zeros are all at
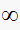 .
.
This tables summarizes the results
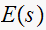 |
|
||||
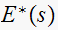 |
|
||||
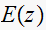 |
|

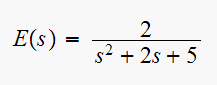
Roots of denominator are
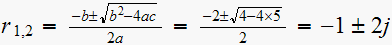
Hence poles of
 are
are
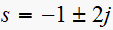 ,
and a non-finite zeros at
,
and a non-finite zeros at
From problem 3-4 (which we did in HW3)
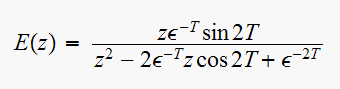
Hence for
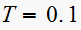 ,
,
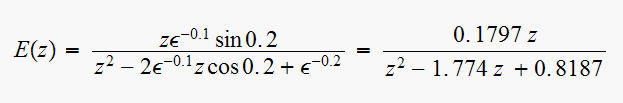
Hence a finite zero is at
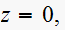 and non-finite zero at
and non-finite zero at
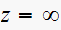 .
(complex infinity). For the poles, the roots of the denominator are found to
be at
.
(complex infinity). For the poles, the roots of the denominator are found to
be at
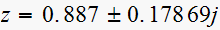
Since we know the poles of
 to be located at
to be located at
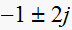 ,
then we can easily find the poles of
,
then we can easily find the poles of
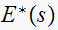 that are periodic with pole
that are periodic with pole
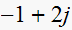 to be at
to be at
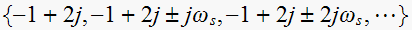 and the poles of
and the poles of
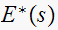 that are periodic with pole
that are periodic with pole
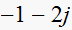 to be at
to be at
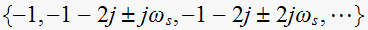
Since
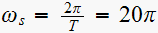 , hence the poles of
, hence the poles of
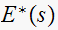 are at
are at
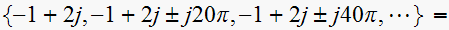
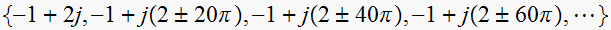
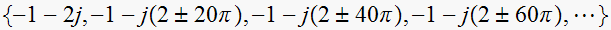
Now to find the zeros of
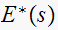 .
Since
.
Since
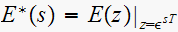 then
then
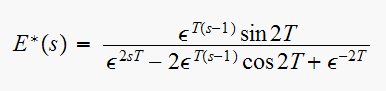
For
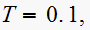
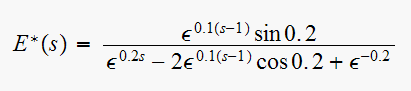
Then we see that a zero of
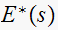 is at
is at
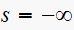 ,
another zero comes when we take the denominator to infinity, which gives a
zero at
,
another zero comes when we take the denominator to infinity, which gives a
zero at
This tables summarizes the results
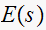 |
|
||||
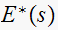 |
|
||||
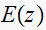 |
|
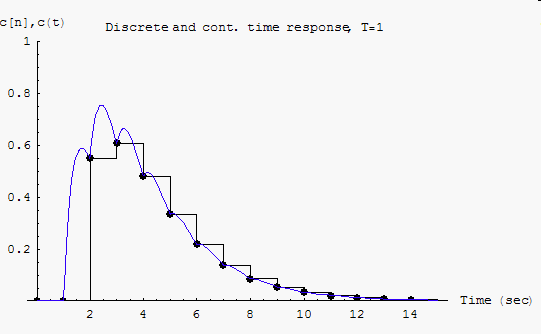
Find the system response at the sampling instances to a unit step input for
the system shown. Plot
 versus time.
versus time.
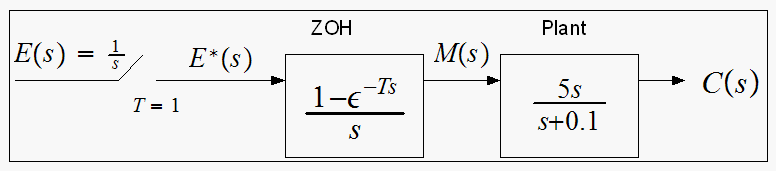
Let plant transfer function be called
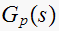
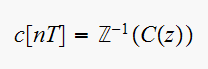
But
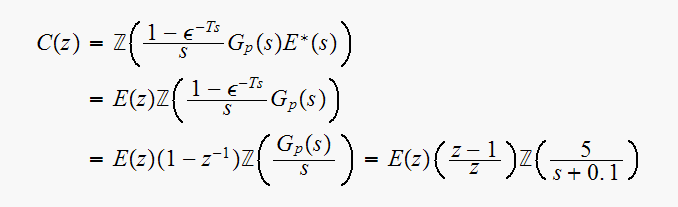
Notice the cancellation of the zero in the plant with the pole from the ZOH.
Now since
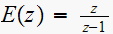 (because
(because
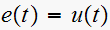 ,
hence
,
hence
![$e[nT]=u[nT]$](graphics/hw4__109.gif) )
)
Then (2) can be written as
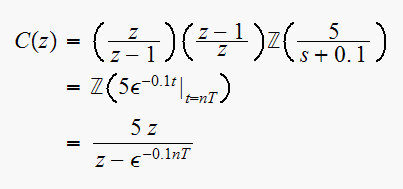
Hence (1) can now be written as
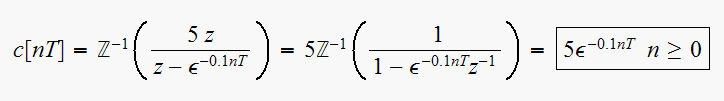
Looking at
![$c[nT]$](graphics/hw4__113.gif) for few values, for
for few values, for
 we get the following sequence generated
we get the following sequence generated
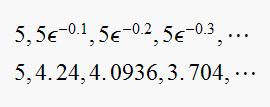
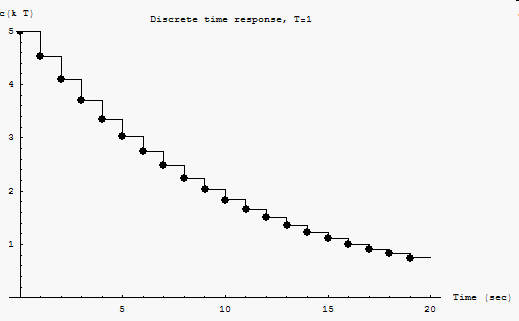
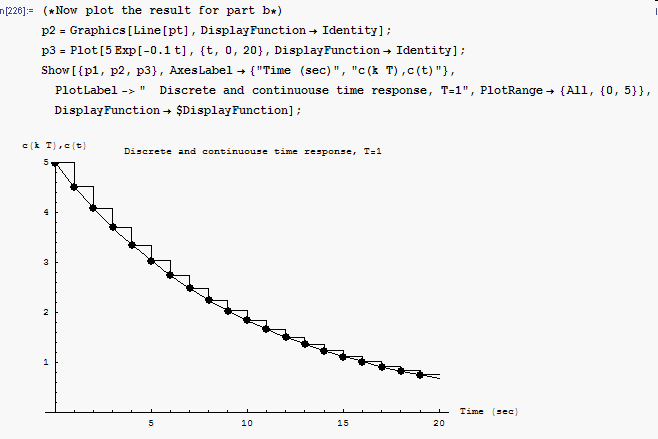
This is a plot of
![$c[nT]$](graphics/hw4__116.gif)
Verify the answer in part(a) by determining the input to the plant
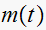 and then calculating
and then calculating
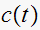 by continuous-time method.
by continuous-time method.
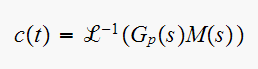
but
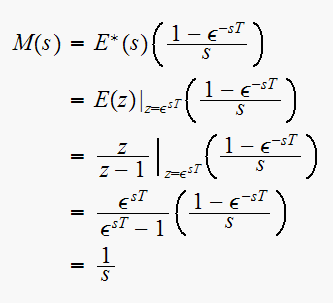
Hence we see that the plant is driven by a unit step, the same as the
reference signal
 itself.
itself.
Now that
 is found, we use (1) to find
is found, we use (1) to find
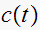
Hence
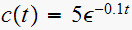
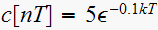
![$u[k]$](graphics/hw4__129.gif)
Here is a plot
Find system response at the sampling instances to a unit-step input for the system shown
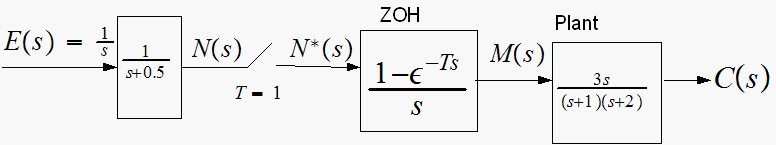
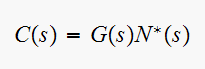
Where
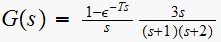
Hence
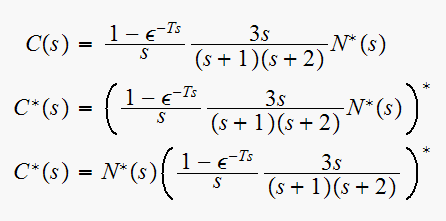
Hence, since all are in star format, we can switch to Z domain
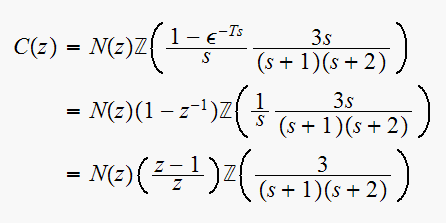
But
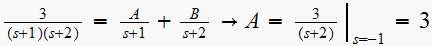 and
and
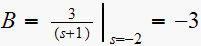
Hence
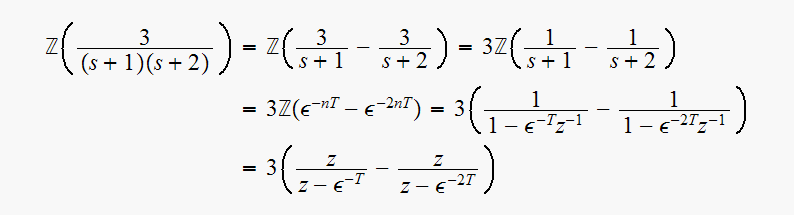
Hence (1) can be written as
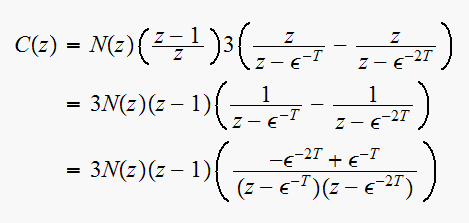
Now need to find
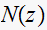 .
But
.
But
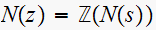
Where
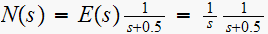
But
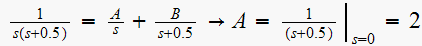 and
and
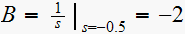
Hence
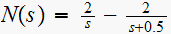
Hence
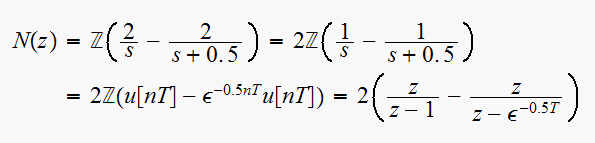
Substitute above into (2) we get
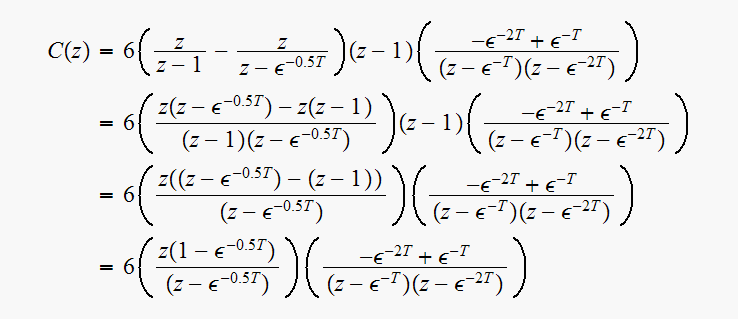
Now Let
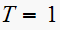 we get
we get
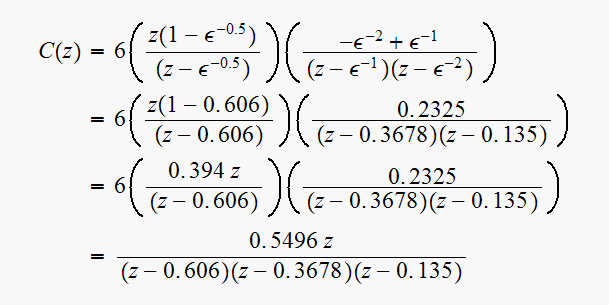
Note that the poles of
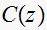 are inside the unit circuit, hence this is a a stable discrete system.
are inside the unit circuit, hence this is a a stable discrete system.
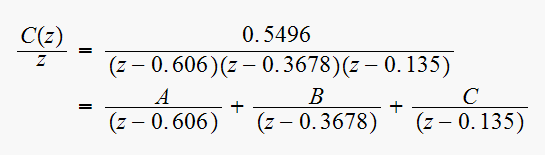
Hence
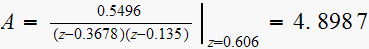
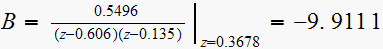
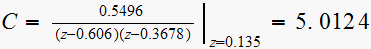
Hence
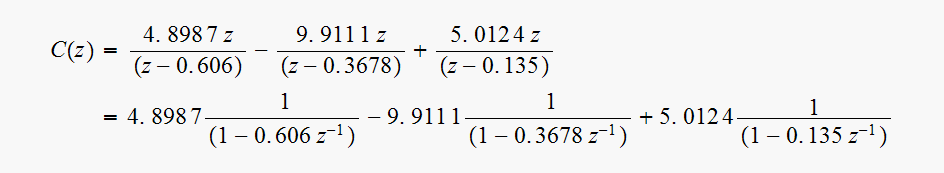
Hence
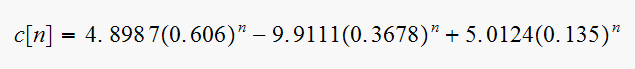
The following is a plot of the response for few values of
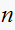
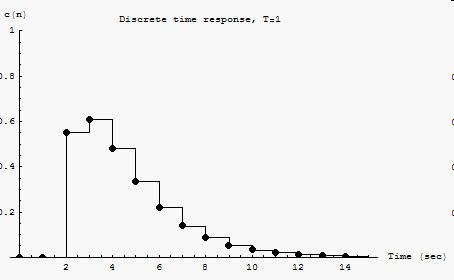
Now I will find
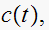 since
since
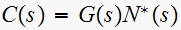 then
then
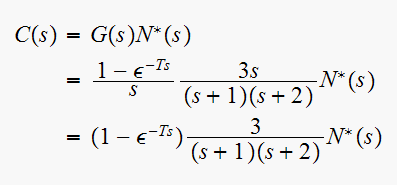
But since
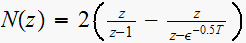 ,
which we found earlier
,
which we found earlier
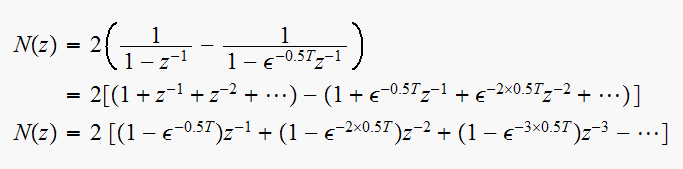
Since a delay
 in Z maps to
in Z maps to
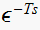 in S, then the above coverts to S domain as
in S, then the above coverts to S domain as
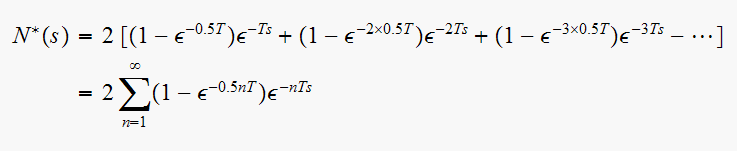
Now (3) can be written as
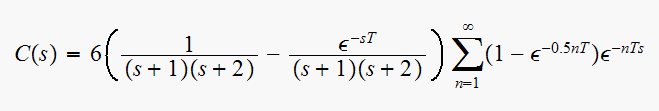
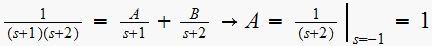 ,
,
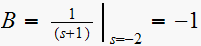
Hence
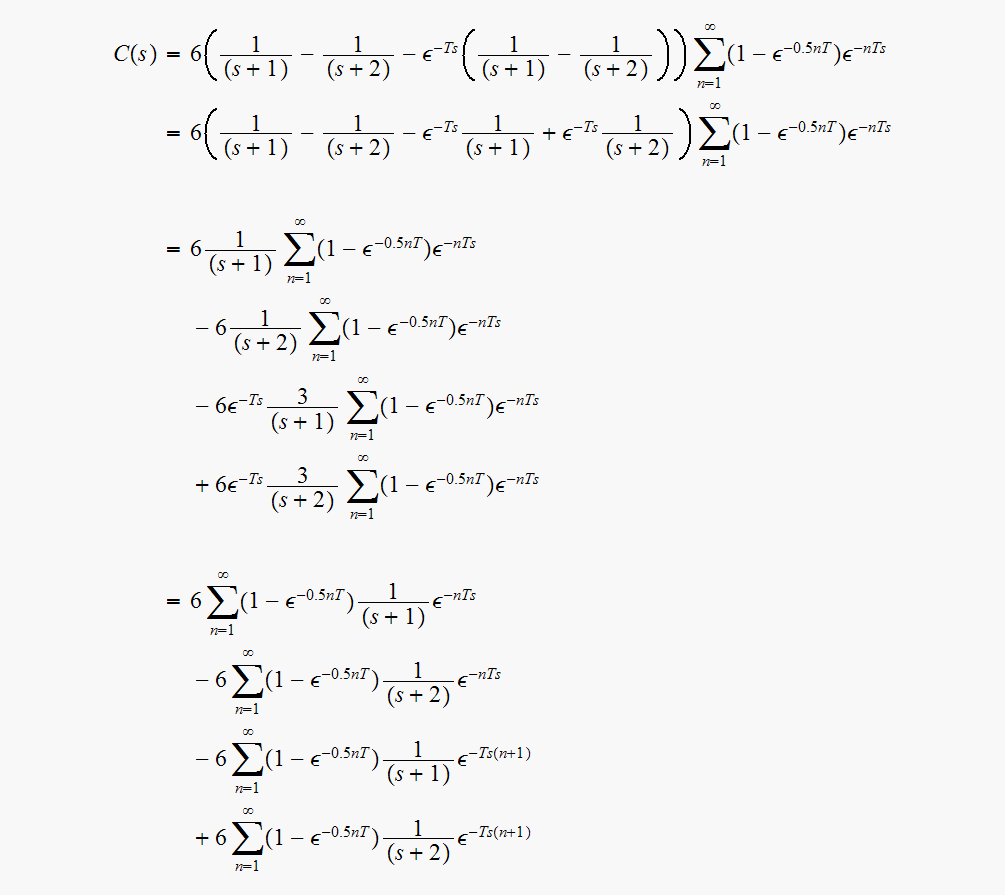
Since
 where
where
Now
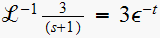 and
and
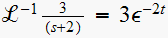
Hence
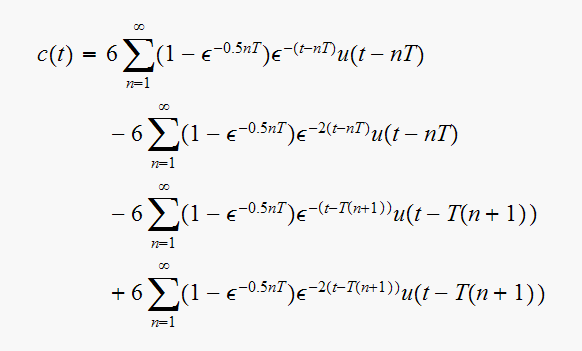
In particular, when
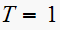 we get
we get
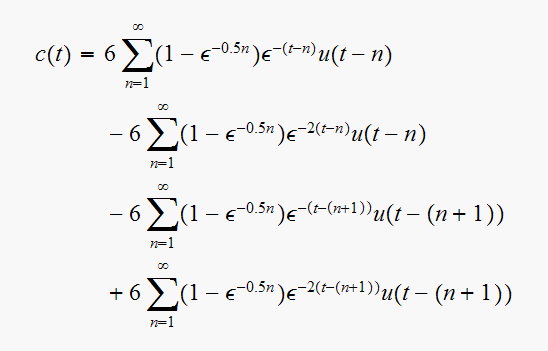
To verify, I plot the above result for
 up to 1000 and for
up to 1000 and for
 up to 15 seconds.
up to 15 seconds.
This is a plot of
 and
and
![$c[n]$](graphics/hw4__181.gif) on the same plot to compare.
on the same plot to compare.
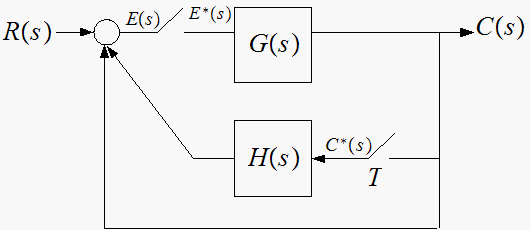
for each system express
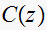 in terms of the input and the transfer functions shown
in terms of the input and the transfer functions shown
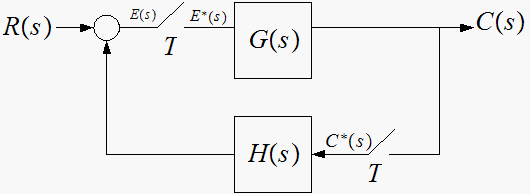
To simplify things, I'll write the symbols without the argument
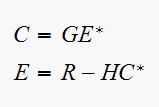
Solve for
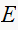 noting that
noting that
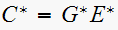
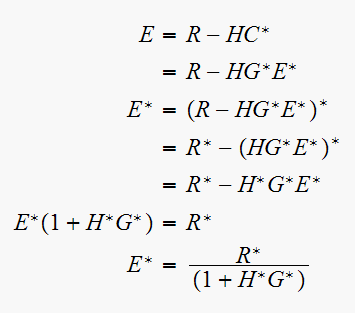
Hence since
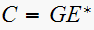 then
then
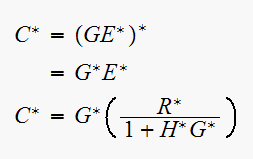
Since now all are starred, then we can convert to
 domain easily
domain easily
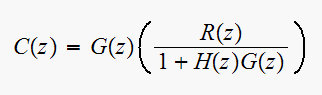
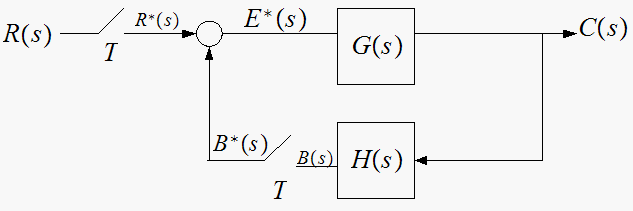
Note that since the error signal Laplace transform is the difference of 2 starred transform, then it is already starred.
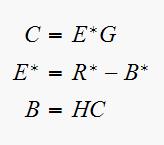
Solve for
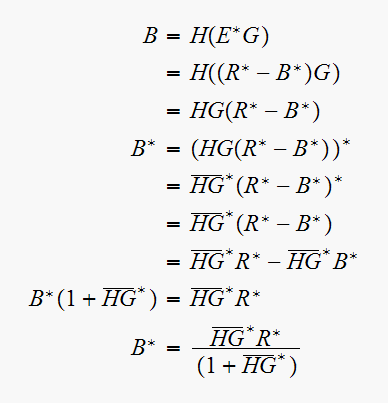
Hence now
since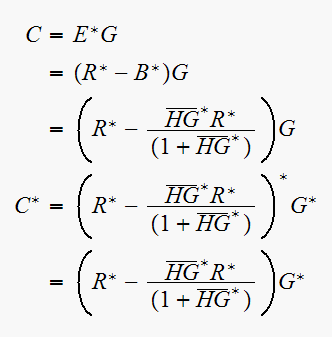
Since all starred, we convert to
 domain
domain
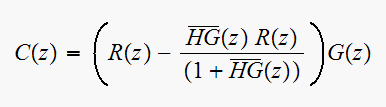
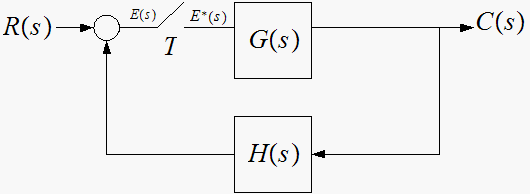
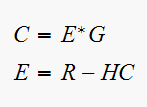
solve for
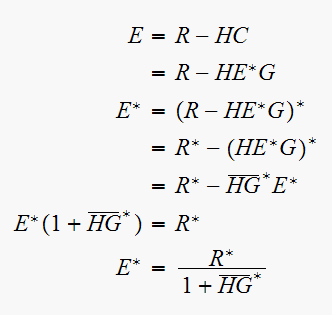
Hence from
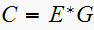 we get
we get
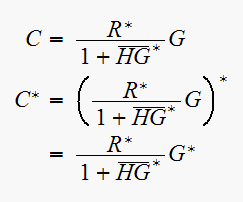
Hence
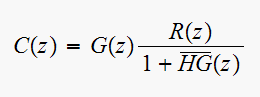
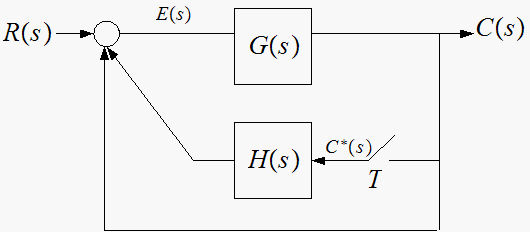
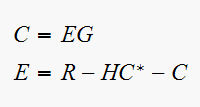
Solve for
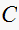
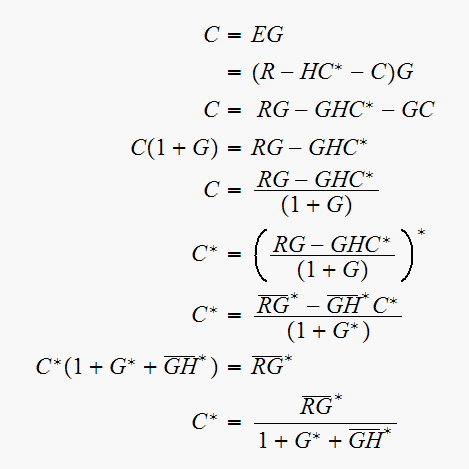
Hence
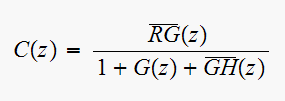
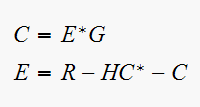
Solve for
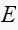
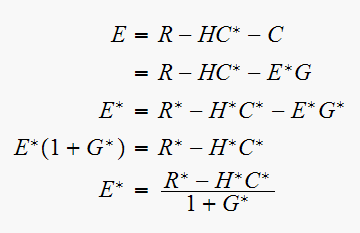
Hence since
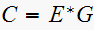 we get
we get
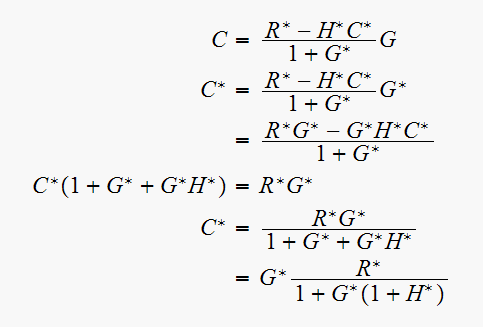
Hence