Physics 229& 100 Homework #9
Name: Nasser Abbasi

1. Use dimensional reasoning and the tools described in Dimensional Analysis  to determine the order of magnitude of several physical quantities.
a) determine the pressure at the center of the earth.

Remove["Global`*"]

<<"MMHTools`DimTools`"

Needs["Miscellaneous`PhysicalConstants`"]

The symbols {c, kB, ℏ, g, G, me, amu, Me, Ms, Na, ε0, μ0, e, σ, Rgas} <br />have been assigned SI unit specifiers

TableForm[Thread[{constantsymbols, symboldefs, symbUnits/constantsymbols}]]

c speed of light Meter/Second
kB Boltzmann's constant Joule/Kelvin
h Planck's constant/2π Joule Second
g acceleration due to gravity Meter/Second^2
G Gravitational constant (Meter^2 Newton)/Kilogram^2
me mass of electron Kilogram
amu mass of proton Kilogram
Me mass of Earth Kilogram
Ms mass of Sun Kilogram
Na Avogadro's number 1/Mole
ε0 permittivity of vacuum (Ampere Second)/(Meter Volt)
μ0 permeability of vacuum (π Second Volt)/(Ampere Meter)
e electron charge Coulomb
σ radiation constant Watt/(Kelvin^4 Meter^2)
Rgas molar gas constant Joule/(Kelvin Mole)

Let d=Radius of earth, ρ denity of earth body, and G is the gravitional constant

dimanal[{ρ   (( Kilogram)/Meter^3), d (Meter), ReduceUnits[ToSymbolsUnits[G]]}, {Kilogram, Meter, Second}, Newton/Meter^2 //ReduceUnits]

{d^2 G ρ^2, {}}

Hence the order of magnitude of pressure at center of earth is

First[%]

d^2 G ρ^2

b) Cooking times for meat are typically given in units such as minutes/pound. This is a fiction devised for the numerically challenged. Using dimensional reasoning, how do you expect the cooking time of a turkey to scale with the mass?

Cooking time should depend on specific heat of turkey c_v (amount of heat to raise its temp by one degree), thermal conductivity of turkey k (how easily heat can flow within the turkey from one spot to another) and size of turkey L

params = {cv (Joule/(Meter^3 Kelvin)), k (Watt/(Meter Kelvin)), L Meter}//ReduceUnits

{(cv Kilogram)/(Kelvin Meter Second^2), (k Kilogram Meter)/(Kelvin Second^3), L Meter}

dimanal[params, {Kilogram, Meter, Second}, Second]

{(cv L^2)/k, {}}

So cooking time depends on the square of the charaterstic length of the turkey. But we are asked to find how cooking time depend on the mass.
Since mass = Volume * density. Taking the density to be uniform and the same among all turkies, we see that the mass is propertional to the volume of the turkey

Hence mass ~ ρ L^3  where ρ is the density

i.e. (mass/ρ)^1/3~ L

But cooking time ~ cv /kL^2

therefore cooking time is ~ (k/C_vmass/ρ)^2/3

In otherwords, cooking time is ~ M^2/3

c) What is the speed of sound in a monotomic gas ?

monatomic gas is one in which atoms are not bound to each other.
Ask the question: What does the speed of sound in such a gas depend on? Answer: Density of gas, Temp. of gas, Pressure P

params = {T (Kelvin), ρ (Kilogram/Meter^3), P (Newton/Meter^2)}//ReduceUnits

{Kelvin T, (Kilogram ρ)/Meter^3, (Kilogram P)/(Meter Second^2)}

dimanal[params, {Kilogram, Meter, Second}, Meter/Second]

{P^(1/2)/ρ^(1/2), {Kelvin T}}

So sound speed ~ P^(1/2)/ρ^(1/2)* f[T]  where f[T] is some function of the temprature of the gass. It is a scalar function, so a f[T] should have some non-dimensional value as a result. I did some research on this and found that for monotomic gas this value is about 1.3 and f[t]=C_p/C_v^(1/2). where C_p is the specific heat of the gas at constant pressure, and C_v is the specific heat of the gas at constant volume

d) Determine the relation between the speed of waves in deep water ( like the ocean) and the wavelength of the waves. (Hint: what is the restoring force for big waves in the ocean?)

Speed of a wave  C = Wave Length (λ) * frequency (f)

i.e. C = λ f

But 2πf=ω

And if we model the wave going up and down as a mass/spring system, with stiffness K, then this leads to the standard formula that ω=K/m^(1/2) where K is the stiffness of the wave as it goes up and down, and M is the mass of each wave.

and we know that  from the mass/spring model that

                      restoring Force = K * displacement
                      
Here the displacement is the average wave hight.

For deep water waves, it is gravity that causes a wave to fall down again after it goes up. Hence the restoring Force is the weight of the wave

                     M g = K * wave height

K= (M g)/h    hence  ω=k/M^(1/2)=g/h^(1/2)
So f=ω/(2π)=g/h^(1/2)1/(2π)

so C = λ f
     C= λ g/h^(1/2)1/(2π)
     
But 2πh = λ  (since one full cycle over the circle of radius h gives the length of the circumeference, which is the wave length).
So       C=  gλ/(2π)^(1/2)


[Graphics:HTMLFiles/index_48.gif]

e) Black holes have a characteristic scale known as the event horizon. Use dimensional reasoning to estimate its size.

What does event horizon depends on?  The event horizon is the distance from the black hole where light does not escape (escape velocity equals the speed of light). Mass of the black hole must be involved, and the universal gravtional constant as well. Therefore, I expect that the size must involve G, Mass, and c

params = {m (Kilogram), G ((Meter^2 Newton)/Kilogram^2), c (Meter/Second)}//ReduceUnits

{Kilogram m, (G Meter^3)/(Kilogram Second^2), (c Meter)/Second}

dimanal[params, {Kilogram, Meter, Second}, Meter]

{(G m)/c^2, {}}

Therefore event horizon ~ (G m)/c^2

2. Boundary value problem : bound states of a quantum particle of mass m in a gravitational field on a hard surface. The Schrodinger equation is  -ℏ^2/(2 m)ψ''[x] + m g x ψ[x] == E ψ[x] . Because the particle is on a hard, impenetrable surface, the boundary condition at x=0 is ψ[0]=0. The other boundary condition is that ψ[x] is square integrable, i.e. ∫_0^∞ψ ψ^*dx=1.  The boundary value problem has solutions only for special values of the energy E. Find the 4 lowest values of E and the associated wave function ψ[x].
a) Use dimanal from MMHTools`DimTools` to determine the natural units of length and energy for this problem. Perform a change of variables ( using Change Variables from MMHTools`DETools`) to express the Schrödinger equation in terms of dimensionless variables.  

Remove["Global`*"] ;

<<"MMHTools`DimTools`"

<<"MMHTools`DETools`"

<<Miscellaneous`PhysicalConstants`

The symbols {c, kB, ℏ, g, G, me, amu, Me, Ms, Na, ε0, μ0, e, σ, Rgas} <br />have been assigned SI unit specifiers

Make symbols for the dimensionless quantities for ease of reading

Needs["Utilities`Notation`"] ;

DynamicSymbolize[f_, k_] := Symbolize[NotationBoxTag[SubscriptBox[f, k]]]

DynamicSymbolize["x", "r"] ;

DynamicSymbolize["ψ", "r"] ;

Now defined the ODE

ode = -( ℏ^2)/(2 m) ψ''[x] + m g x ψ[x] == En ψ[x]

g m x ψ[x] - (ℏ^2 ψ^′′[x])/(2 m) == En ψ[x]

The parameters involved in the ODE are m,g,  h and E

condp = {m Kilogram, g ,   ℏ}//ToSymbolsUnits//ReduceUnits

{Kilogram m, (g Meter)/Second^2, (Kilogram Meter^2 ℏ)/Second}

Find what is the length x is propertional to (this is the independent variable)

dimanal[condp, {Kilogram, Meter, Second, Coulomb}, Meter]

{ℏ^(2/3)/(g^(1/3) m^(2/3)), {}}

mainTerm = First[%]

ℏ^(2/3)/(g^(1/3) m^(2/3))

Hence Δx= xr(ℏ^(2/3)/(g^(1/3) m^(2/3)))  where xr is the constant of propertionality
Do a change of variable to change x in the ODE to the above

ode1 = ChangeVariable[ode, x→x_r (mainTerm), ψ, ψ, x, x_r]

1/2 g^(2/3) m^(1/3) ℏ^(2/3) (2 x_r ψ[x_r] - ψ^′′[x_r]) == En ψ[x_r]

Now change the energy E  to be dimensionless

dimanal[condp, {Kilogram, Meter, Second, Coulomb}, ReduceUnits[Joule]]

{g^(2/3) m^(1/3) ℏ^(2/3), {}}

mainTerm = First[%]

g^(2/3) m^(1/3) ℏ^(2/3)

So E~ er * g^(2/3) m^(1/3) ℏ^(2/3)  

ode2 = ChangeVariable[ode1, En→λ (mainTerm) , ψ, ψ_r, x_r, x_r]

g^(2/3) m^(1/3) ℏ^(2/3) (-2 (x_r - λ) ψ_r[x_r] + ψ_r^′′[x_r]) == 0

We see from the above that we get g^(2/3) m^(1/3) ℏ^(2/3)  Times expression of the reduced ODE ==0. Hence we can divide both sides by g^(2/3) m^(1/3) ℏ^(2/3) to remove it, we get

ode2 = ode2/.mainTerm→1

-2 (x_r - λ) ψ_r[x_r] + ψ_r^′′[x_r] == 0

ode2 = Simplify[ode2]

2 (x_r - λ) ψ_r[x_r] == ψ_r^′′[x_r]

The above represents the ODE in its dimensionless form. λ is now the eigenvalue of the ODE

b) Use finite differences to estimate  the first few eigenvalues, and plot the first 4 eigenfunctions.  ( use finitedifEVP from the Boundary Value Problems notebook; either copy and paste into this notebook, or execute the relevant lines in the browser. ) Explain how you deal with the boundary condition at ∞.

Needs["LinearAlgebra`MatrixManipulation`"] ;

General :: spell1 : Possible spelling error: new symbol name \"evals\" is similar to existing symbol \"bvals\". More…

General :: spell1 : Possible spelling error: new symbol name \"offset\" is similar to existing symbol \"Offset\". More…

I used ψ[xFarWay]==0 as the upper boundary condition. Becuase that should be far enough to approximate infinity for this problem. The square integrable B.C. tells us that the solution should be zero far away.

xFarEnough = 100 ;

{evc, evcs} = finitedifEVP[ode2, {ψ_r[0] == 0, ψ_r[xFarEnough] == 0}, {0, xFarEnough}, λ, ψ_r, x_r, 4, False]

General :: spell : Possible spelling error: new symbol name \"evcs\" is similar to existing symbols {evc, evecs} . More…

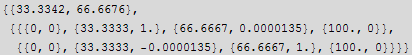
{{33.3342, 66.6676}, {{{0, 0}, {33.3333, 1.}, {66.6667, 0.0000135}, {100., 0}}, {{0, 0}, {33.3333, -0.0000135}, {66.6667, 1.}, {100., 0}}}}

evcs//TableForm

0
0
33.3333
1.
66.6667
0.0000135
100.
0
0
0
33.3333
-0.0000135
66.6667
1.
100.
0

evc//TableForm

33.3342
66.6676

c) Solve the same equation using the shooting method. The shooting method also requires a finite interval.  Recall that the shooting method can be unstable for large values of xr, so you may need to experiment with the appropriate form of the boundary conditon at the right hand boundary.

ψp0 = 1 ;

ode2

2 (x_r - λ) ψ_r[x_r] == ψ_r^′′[x_r]

Solve using shooting method by looking for solution that makes ψ goes to zero far away. I used x=100 value to represent far away or infinity.

[Graphics:HTMLFiles/index_110.gif]

The above shows where ψ(x) will be zero as a function of the eigenvalue λ. Now use FindRoot to find the smallest 4 eigenvalues

FindRoot[ψAtFar[ψp0, λ], {λ, 5}]

{λ→5.43261}

FindRoot[ψAtFar[ψp0, λ], {λ, 20}]

{λ→20.2399}

FindRoot[ψAtFar[ψp0, λ], {λ, 45}]

{λ→44.9136}

FindRoot[ψAtFar[ψp0, λ], {λ, 80}]

{λ→79.4571}

d) This problem is somewhat unusual because an exact analytical solution can be found. Use DSolve to find analytic expressions for the eigenfucntions, and use FindRoot to numerically estimate the eigenvalues. Hint: solve the problem without imposing the boundary conditions. The solution will be a linear combination of two functions. Argue that one of them diverges at x-> ∞, so cannot be part of the solution. Then find the values of er which satisfy the boundary condition at xr=0.

sol = ψ_r[x_r]/.Flatten[DSolve[ode2, ψ_r[x_r], x_r]]

AiryAi[(2 x_r - 2 λ)/2^(2/3)] C[1] + AiryBi[(2 x_r - 2 λ)/2^(2/3)] C[2]

Now I have 2 solutions being added togother to give a general solution. From the boundary condition that tells us ∫_0^∞ψ ψ^*dx=1 it implies that solution is zero at zero, and also zero at far away. So I plot each of the above solutions, then see which solution blow up as x gets large. Then I discard this solution since it would not lead to the boundary condition given.

Plot[AiryAi[x], {x, 0, 10}, PlotRange→All] ;

[Graphics:HTMLFiles/index_124.gif]

So the above tells me that I need to keep the solution associated with AiryAi, which is the solution that is associated with C[1]. Now look the second solution

Plot[AiryBi[x], {x, 0, 10}, PlotRange→All] ;

[Graphics:HTMLFiles/index_126.gif]

We see that AiryBi blows up, hence C[2] must be zero to avoid this solution. Hence solution is

sol = sol/.first_ + second_→first

General :: spell1 : Possible spelling error: new symbol name \"first\" is similar to existing symbol \"First\". More…

AiryAi[(2 x_r - 2 λ)/2^(2/3)] C[1]

Since C[1] is a constant, I can set it to 1

sol = sol/.C[1] →1

AiryAi[(2 x_r - 2 λ)/2^(2/3)]

So the above now is the solution for ψ. there is an eigenvalue λ that the solution depends on. Now find λ which makes this solution go to zero at x_r=0

sol = sol/.x_r→0

AiryAi[-2^(1/3) λ]

Plot[sol, {λ, 0, 10}] ;

[Graphics:HTMLFiles/index_136.gif]

We now can find few λ's which will make the solution ψ be zero at zero bu using FindRoot

FindRoot[sol, {λ, 2}]

{λ→1.85576}

FindRoot[sol, {λ, 5}]

{λ→5.38661}

FindRoot[sol, {λ, 6.5}]

{λ→6.30526}

Ok, problem completed.

3. Find a representation in terms of Fourier series for the periodic function with period 1 which is generated by semicircles as shown in the Figure below. Make a plot which compares the function and the series approximation.

[Graphics:HTMLFiles/index_143.gif]

Since the function is periodic, it can be expanded by Fourier series, since a fourier series approximates periodic functions only.

Plot the above function

Remove["Global`*"]

Needs["Graphics`Colors`"] ;

<<Graphics`Animation`

r = .5 ;   y0 = .5 ; x0 = 0.5 ;

fMain[x_] := If[x<=0., 0, base = Floor[x] ; newX = x - base ; N[-(r^2 - (newX - x0)^2)^(1/2) + y0]] ;

fOnePeriod[x_] := Piecewise[{   {0, x≤ 0}, {N[-(r^2 - (x - x0)^2)^(1/2) + y0 ], 0≤x< 1}, {0 , 1≤x}}]

Plot[fMain[x], {x, 0, 3}, AxesOrigin→ {0, 0}, AspectRatio→Automatic, PlotLabel->"f[x] over many periods", ImageSize→500] ;

[Graphics:HTMLFiles/index_151.gif]

Plot[fOnePeriod[x], {x, 0, 3}, AxesOrigin→ {0, 0}, AspectRatio→Automatic, PlotLabel->"f[x] over one period", ImageSize→500] ;

[Graphics:HTMLFiles/index_153.gif]

generate a list of the a[n] and b[n].

maxN = 10 ; (*10 terms is more than enough to get very good approximation*)from = 0 ;

to = 1 ;

period = 1 ; (*Always use the period of the function we want to approximate*)a0 = 1/period/2NIntegrate[fOnePeriod[x], {x, from, to}] ;

a = Chop[N[Table[1/period/2∫_from^toCos[(n π x)/period/2] fOnePeriod[x] x, {n, 1, maxN}]]] ;

b = Chop[N[Table[1/period/2∫_from^toSin[(n π x)/period/2] fOnePeriod[x] x, {n, 1, maxN}]]] ;

xseries[x_, maxN_] := 1/2a0 + Underoverscript[∑, n = 1, arg3] (  a[[n]] Cos[(n π x)/period/2] + b[[n]] Sin[(n π x)/period/2] ) ;

Now plot the approximation over one period of the function

[Graphics:HTMLFiles/index_161.gif]

[Graphics:HTMLFiles/index_162.gif]

[Graphics:HTMLFiles/index_163.gif]

[Graphics:HTMLFiles/index_164.gif]

[Graphics:HTMLFiles/index_165.gif]

[Graphics:HTMLFiles/index_166.gif]

[Graphics:HTMLFiles/index_167.gif]

[Graphics:HTMLFiles/index_168.gif]

[Graphics:HTMLFiles/index_169.gif]

[Graphics:HTMLFiles/index_170.gif]

Now plot the approximation over many periods

[Graphics:HTMLFiles/index_172.gif]

[Graphics:HTMLFiles/index_173.gif]

[Graphics:HTMLFiles/index_174.gif]

[Graphics:HTMLFiles/index_175.gif]

[Graphics:HTMLFiles/index_176.gif]

[Graphics:HTMLFiles/index_177.gif]

[Graphics:HTMLFiles/index_178.gif]

[Graphics:HTMLFiles/index_179.gif]

[Graphics:HTMLFiles/index_180.gif]

[Graphics:HTMLFiles/index_181.gif]

Function for animation

these below are animations.

AnimateToClosedGroup[plotlist, .5]

[Graphics:HTMLFiles/index_195.gif]

Below is animation of the whole function

AnimateToClosedGroup[plotlist, .5]

[Graphics:HTMLFiles/index_208.gif]

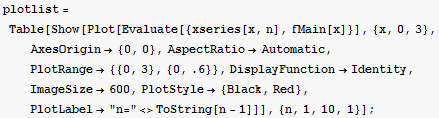
4.  A triangle function is zero for  |x|>a, and has magnitude L at x=0 as shown in the figure.

[Graphics:HTMLFiles/index_209.gif]

Calculate the Fourier transform of this function.

Since the function is not periodic, it can not be approximated by Fourier series since a fourier series approximates periodic functions only. We need to use fourier transform.

Remove["Global`*"] ;

Do a sketch to make sure I got the function definition ok first. Pick some values for 'a' and 'L'

a = 3 ;

L = 1 ;

f[x_] := Piecewise[{   {0, x< -a}, {0, x>a}, {L + (L/a) x, -a≤ x<0}, {L - L/ax, 0≤ x<a}}]

Plot[f[x], {x, -4, 4}, AxesOrigin→ {0, 0}] ;

[Graphics:HTMLFiles/index_215.gif]

It looks Ok, now write the fourier transform

g[ω_] := 1/(2π) ∫_ (-a)^af[x] ^(- ω x) x

Plot[Evaluate[g[ω]], {ω, -10, 10}, PlotRange→All, AxesLabel→ {"ω", "F[ω]"}] ;

[Graphics:HTMLFiles/index_218.gif]

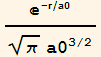5(grads). The wave function for the electron in the ground state of hydrogen is ψ_1(r)=^(-r/a0)/(π^(1/2) a0^(3/2)), where a0 is a unit of length (Bohr radius) and r is the spherical position coordinate.
a) Verify that this wave function is normalized.

b)  ψ_1(r) lives in 3 dimensional space. The Fourier transform ψ_1(k)=1/(2π)^(3/2)∫ ^( Overscript[k, →] ·Overscript[x, →]) ψ_1(r) d^3x lives in 3 dimensional k space; ψ_1(k) represents the amplitude to have a momentum p=h k.   Choose a coordinate system with the z axis aligned along Overscript[k, →], and perform the integration.

c) verify that ψ_1(k) is normalized. ψ_1(k)ψ_1^*(k) is the probability density of k. What is the most probable value of the magnitude of k?

6. Make a plot of the prime interest rate as a function of time from 1949  to the present. The data can be found at http://www.federalreserve.gov/releases/h15/data.htm  ( go to Bank prime loan and click on Monthly). Use your browser , and "save as" to save a copy of the file on your local hard drive. Use Drop to remove the header information. You will have to convert data records such as 01/1949 , which are strings, into numbers. Use decimal years , so the string 01/1949 should be represented as 1949.08.  Process the data using pattern matching,  Take, Drop, and StringTake. ToExpression will convert strings into numbers.

Remove["Global`*"]

localdata = "E:\\nabbasi\\data\\nabbasi_web_Page\\my_courses\\UCI_COURSES\\CREDIT_COURSES\\fall_2006\\PHYS_100_comp_physics\\HWs\\HW9" ;

data = Import[localdata<>"\\H15_PRIME_NA.txt", "Lines"] ;

Dimensions[data]

{703}

Find which line number the header goes to, by trial and error

data[[8]]

DATE      , PRIMENA

data[[9]]

01/1949, 2.00

So I need to remove the first 8 lines

data = Drop[data, 8] ;

data[[1]]

01/1949, 2.00

Ok, now data has only rows of actual data to use. Now convert date such as 01/1949 to 1949.08

cleanData = {} ;

This function below parses ONE line. It is called by the main loop. It takes one line and returns a list of 2 entries. One for the date in correct decimal format, and the second entry is the interest rate. all converted to numbers.

This is the main program below. It called the above function in a loop to process all lines

Do[AppendTo[cleanData, processLine[data[[n]]]], {n, 1, Length[data]}] ;

Now plot it

[Graphics:HTMLFiles/index_248.gif]

Created by Mathematica  (January 30, 2007) Valid XHTML 1.1!