Physics 229& 100 Homework #7
Name: Nasser Abbasi

1. Consider the problem of a mass m on a spring of spring constant k subject to a force which is zero until t=0 and is equal to Sin[ωt] for t>0. We want to consider cases where ω=ω_0=(k/m)^(1/2), and cases where ω is slightly different from ω_0. This is a simple mechanical model for an atom illuminated by near-resonant laser light.

a) To exercise your intuition, first sketch what you think the two solutions will look like; use PowerPoint or some other drawing package ( Paint if you have to) , and include the sketch of your expectations here.

For the case when the forcing frequency marches the natural frequency, resonance will occure. The mass will obtain maximum amplitude. When the forcing frequnecy is different from the natural frequency, then the mass will vibrate in sinuosidel manner (harmonic motion). This is sketch using paint (sorry about the bad quality, hard to write/draw using a mouse).
the y-axis is the displacement y(t). We see that when w=x_n, then the displacement will continue to grow.

[Graphics:HTMLFiles/index_4.gif]

b) Then use the greens function derived in class to make a plot of the position as a function of time for the case  ω=ω_0=2, m=1. Contrast this with the case in which the force is Sin[0.9*ω_0t] for t>0, i.e. off resonance illumination.

Due to the divide by zero problem when w=2 exactly (resonance), will plot value very near resonance first.
Since w_n=k^(1/2)/m^(1/2) then k=m w_n^2m , hence for w=2, m=1, we get k=4

p1 = Plot[Evaluate[y[t]/.{m→1, ω→1.99999, k→4}], {t, 0, 60}, AxesLabel→ {"t", "y(t)"}, PlotStyle→Red, DisplayFunction→Identity] ;

Show[p1, DisplayFunction→$DisplayFunction]

[Graphics:HTMLFiles/index_13.gif]

-Graphics -

Notice also there is what is called 'beats' within the exponentional increasing motion. We see this by plotting for large t

Plot[Evaluate[y[t]/.{m→1, ω→1.99999, k→4}], {t, 0, 400}, AxesLabel→ {"t", "y(t)"}]

[Graphics:HTMLFiles/index_16.gif]

-Graphics -

Now plot for 0.9 w

p2 = Plot[Evaluate[y[t]/.{m→1, ω→0.9 * 2, k→4}], {t, 0, 65}, AxesLabel→ {"t", "y(t)"}, DisplayFunction→Identity] ;

Show[p2, DisplayFunction→$DisplayFunction]

[Graphics:HTMLFiles/index_20.gif]

-Graphics -

Put both plots together

Show[{p1, p2}, PlotLabel->"Comparing y(t) for resonance (RED) to non-resonance", DisplayFunction→$DisplayFunction]

[Graphics:HTMLFiles/index_23.gif]

-Graphics -

2. Consider a linear  molecule as shown above  ( like acetylene). Write the Lagrangian for motions along the line in terms of the masses and spring constants. There are two different kinds of bonds, so there are two different spring constants. To make this very clear, copy the graphic into PowerPoint and add text to denote spring constants kHC and kCC , and masses mC and mH, and then re-import the graphic by copying and pasting.

[Graphics:HTMLFiles/index_25.gif]

a) Use EulerEquations to generate the equations of motion.

Remove["Global`*"]

v1 = x[1] '[t] ;

v2 = x[2] '[t] ;

v3 = x[3] '[t] ;

v4 = x[4] '[t] ;

KE = 1/2mH v1^2 + 1/2mC v2^2 + 1/2mC v3^2 + 1/2mH v4^2

1/2 mH x[1]^′[t]^2 + 1/2 mC x[2]^′[t]^2 + 1/2 mC x[3]^′[t]^2 + 1/2 mH x[4]^′[t]^2

PE = 1/2kHC (x[1][t] - x[2][t])^2 + 1/2kCC (x[2][t] - x[3][t])^2 + 1/2kHC (x[3][t] - x[4][t])^2

1/2 kHC (x[1][t] - x[2][t])^2 + 1/2 kCC (x[2][t] - x[3][t])^2 + 1/2 kHC (x[3][t] - x[4][t])^2

L = KE - PE//Simplify

1/2 (-kHC (x[1][t] - x[2][t])^2 - kCC (x[2][t] - x[3][t])^2 - kHC (x[3][t] - x[4][t])^2 + mH x[1]^′[t]^2 + mC x[2]^′[t]^2 + mC x[3]^′[t]^2 + mH x[4]^′[t]^2)

Needs["Calculus`VariationalMethods`"]

deps = {x[1][t], x[2][t], x[3][t], x[4][t]} ;

(eqs = EulerEquations[L, deps, t])//MatrixForm

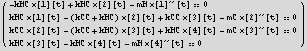
I can also display the above EQM is a more standard format as follows (even though this is not needed to procceed)

Needs["LinearAlgebra`MatrixManipulation`"]

vars = {x[1] ''[t], x[2] ''[t], x[3] ''[t], x[4] ''[t]} ;

{massMatrix, b} = LinearEquationsToMatrices[eqs, vars] ;

{stiffnessMatrix, doNotCare} = LinearEquationsToMatrices[b, deps] ;

Print[MatrixForm[massMatrix], MatrixForm[Transpose[List[vars]]], "+", MatrixForm[stiffnessMatrix], MatrixForm[Transpose[List[deps]]], "== 0"]

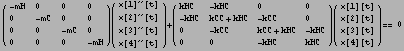
b) Try to use DSolve to solve the resulting system of equations.

(sol = Flatten[DSolve[eqs, deps, t]])//MatrixForm

$Aborted

c) Depending on which version of Mathematica you are running, you will either paralyze the machine or generate quite a lot of gibberish. Now convert the systems of equations to an eigenvalue problem and determine the eigenfrequencies and normal modes of the molecule. This problem is slightly different from the previous ones we discussed because the masses are not all identical, so be careful about the relationship between the eigenvalues and the eigenfrequencies.

Substitute trial solution x(t)= a exp(i w t) into the system of equations

(trialsol = Thread[Table[x[i], {i, 1, 4}] ->Table[Function[t, Evaluate[a[i] E^(I ω t)]], {i, 1, 4}]])//TableForm

x[1] →Function[t, ^( t ω) a[1]]
x[2] →Function[t, ^( t ω) a[2]]
x[3] →Function[t, ^( t ω) a[3]]
x[4] →Function[t, ^( t ω) a[4]]

(eqOfMotionAfterSub = eqs/.trialsol)//TableForm

-^( t ω) kHC a[1] + ^( t ω) mH ω^2 a[1] + ^( t ω) kHC a[2] == 0
^( t ω) kHC a[1] - ^( t ω) (kCC + kHC) a[2] + ^( t ω) mC ω^2 a[2] + ^( t ω) kCC a[3] == 0
^( t ω) kCC a[2] - ^( t ω) (kCC + kHC) a[3] + ^( t ω) mC ω^2 a[3] + ^( t ω) kHC a[4] == 0
^( t ω) kHC a[3] - ^( t ω) kHC a[4] + ^( t ω) mH ω^2 a[4] == 0

Eliminate common factor e^iwt

(eqOfMotionAfterSub = eqOfMotionAfterSub/.qx_ == 0:→Simplify[qx * E^(-I ω t)] == 0)//TableForm

mH ω^2 a[1] + kHC (-a[1] + a[2]) == 0
kHC (a[1] - a[2]) + mC ω^2 a[2] + kCC (-a[2] + a[3]) == 0
kCC (a[2] - a[3]) + mC ω^2 a[3] + kHC (-a[3] + a[4]) == 0
kHC (a[3] - a[4]) + mH ω^2 a[4] == 0

eigVectorComponents = {a[1], a[2], a[3], a[4]} ;

{massStiffnessMatrix, doNotCare} = LinearEquationsToMatrices[eqOfMotionAfterSub, eigVectorComponents] ;

Print[MatrixForm[massStiffnessMatrix], MatrixForm[Transpose[List[eigVectorComponents]]], "== 0"]

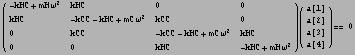
Now Solve Det[K-w^2 M]==0 to find eigen frequencies. Then for each eigenFrequency, solve for eigenMode V from equation (K-w^2M)*V=0
The matrix I called massStiffnessMatrix above is the same as   [ k-w^2 M ]
But first replace w^2 by λ

charEquation = massStiffnessMatrix/.ω^2→λ ;

charEquation = Det[charEquation] == 0

eigFreq = Flatten[Solve[charEquation, λ]] ;

eigFreq = eigFreq[[All, 2]]

eigFreq = eigFreq^(1/2)

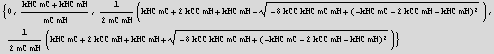
For each eigenfrequency, sub back into m2 and find eigen vectors. Use NullSpace for this

eigVector = Table[0, {4}] ;

Do[Print["Normal Mode for freq ", eigFreq[[i]], " is ", eigVector[[i]] = Simplify[NullSpace[massStiffnessMatrix/.ω→eigFreq[[i]]]]], {i, 1, 4}]

Normal Mode for freq 0 is {{1, 1, 1, 1}}

Normal Mode for freq (kHC mC + kHC mH)/(mC mH)^(1/2) is {{1, -mH/mC, -mH/mC, 1}}

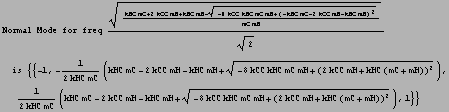
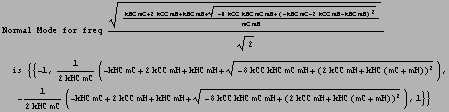
To see the eigenmodes better, I use some numerical values for mass and stiffness and then do an animation

(*pick some values *)kHC = 5 ; kCC = 2 ; mC = 50 ; mH = 20 ; N[eigVector]//MatrixForm

( {{( {{1.}, {1.}, {1.}, {1.}} )}, {( {{1.}, {-0.4}, {-0.4}, {1.}} )}, {( {{-1.}, {-0.787765}, {0.787765}, {1.}} )}, {( {{-1.}, {0.507765}, {-0.507765}, {1.}} )}} )

This below is extra. It is animation of each eigen mode.

Needs["Calculus`VariationalMethods`"]

Needs["Graphics`Animation`"]

Needs["Graphics`Graphics`"] (*This function is from the Prof . book, from the Case studies notebook*)

(*pick some values *)kHC = 5 ; kCC = 2 ; mC = 100 ; mH = 20 ; chain = {eigFreq, 2 * Flatten[eigVector, 1]} ; (*I mutiply the eigVector by 2 to make it bigger to see better*)

Now animate each mode. The first one is not interesting as nothing will move

animate[chain, 1]

[Graphics:HTMLFiles/index_296.gif]

animate[chain, 2]

[Graphics:HTMLFiles/index_468.gif]

animate[chain, 3]

[Graphics:HTMLFiles/index_766.gif]

animate[chain, 4]

[Graphics:HTMLFiles/index_937.gif]

3.  "Shoot the monkey" is a popular physics demonstration in which a projectile is shot from a gun which is aimed directly at a monkey which is in a nearby tree. The monkey tries to avoid being shot by dropping from the tree the moment the projectile is fired. Both the projectile and the monkey are subject to gravity so the poor monkey gets nailed anyway, much to the delight of the freshmen. Make an animation that shows this. Use the projectile example in Plotting&GraphicsExamples.nb as a guide. Model both the projectile and the monkey as a circle or disk.

The equation of motion for the projectile:
Assume the projectile starts from position coordinates (0,h). Assume the initial speed is v_x in the x-direction and v_y in the y-direction. Hence the position of the project at time t will be given by x=v_xt and y=h+v_yt-1/2gt^2
For the falling monkey. Let its initial position be given by (a,h), hence at any time t afterwords, its position is given by x=a  and y=h-1/2gt^2

Remove["Global`*"]

Needs["Graphics`Animation`"] h = 40 ; (*m*)a = 70 ; (*m*)v_x = 30 ; (*m/sec*)v_y = 0 ; (*m/sec*)g = 9.8 ; (*m/sec^2*)

Now generate the (x,y) coordinates for the projectile

xyProjectile = Table[{v_x t, h + v_y t - 1/2g t^2}, {t, 0, 2.5, 0.02}] ;

xyMonkey = Table[{a, h - 1/2g t^2}, {t, 0, 5, 0.02}] ;

r = 0.5 ;

ShowAnimation[t] ;

SelectionMove[EvaluationNotebook[], All, GeneratedCell] ;

    FrontEndTokenExecute["CellGroup"] ;

      FrontEndTokenExecute["OpenCloseGroup"]

[Graphics:HTMLFiles/index_1082.gif]

4. Practice in understanding power series solutions:  The differential equation y''[x] +y'[x] Sin[x] +y[x]==0 has analytic coefficients and therefor has two independent solutions which can be expressed as a power series. First note that DSolve can not solve the equation. Then construct a solution "by hand" , by explicitly substituting a power series trial solution, expanding the resulting expression as a power series, equating the coefficient of each power of x to zero, and solving the resulting equations. Find the first 15 terms in the series. Remember that the equation must have two constants of integration, which can be taken to be y[0] and y'[0].

Remove["Global`*"] ;

ode = y''[x] + y '[x] Sin[x] + y[x] ;

DSolve[{ode == 0, y '[0] == 0, y[0] == 0}, y[x], x]

DSolve[{y[x] + Sin[x] y^′[x] + y^′′[x] == 0, y^′[0] == 0, y[0] == 0}, y[x], x]

Now use a power series as a trial solution and plug in the ode as well

trialSeriesSolution = Underoverscript[∑, i = 0, arg3] a[i] x^i

a[0] + x a[1] + x^2 a[2] + x^3 a[3] + x^4 a[4] + x^5 a[5] + x^6 a[6] + x^7 a[7] + x^8 a[8] + x^9 a[9] + x^10 a[10] + x^11 a[11] + x^12 a[12] + x^13 a[13] + x^14 a[14] + x^15 a[15]

seriesODE = ode/.y→Function[x, Evaluate[trialSeriesSolution]]

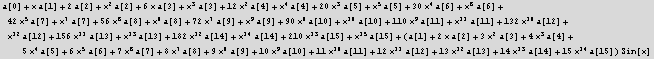
Now apply Series command again on the above to expand the Sin[x] term

seriesODE = Series[seriesODE, {x, 0, 15}]

Collect[%, x]

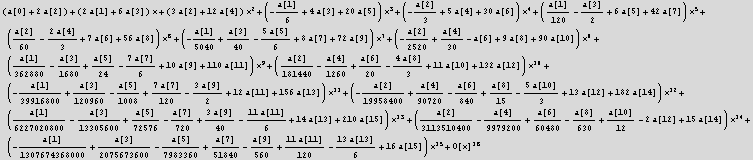
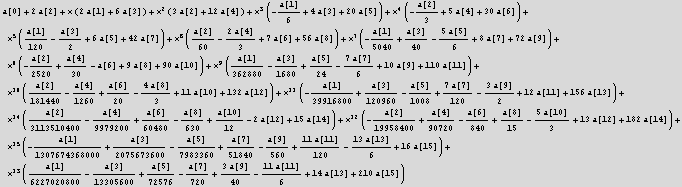
Now generate set of algebraic equations to solve for the a[i] coeff.  

(seriesEqs = Table[Coefficient[seriesODE, x, i] == 0, {i, 0, 15}])//TableForm

a[0]+2 a[2]==0
2 a[1]+6 a[3]==0
3 a[2]+12 a[4]==0
-a[1]/6 + 4 a[3] + 20 a[5] == 0
-a[2]/3 + 5 a[4] + 30 a[6] == 0
a[1]/120 - a[3]/2 + 6 a[5] + 42 a[7] == 0
a[2]/60 - (2 a[4])/3 + 7 a[6] + 56 a[8] == 0
-a[1]/5040 + a[3]/40 - (5 a[5])/6 + 8 a[7] + 72 a[9] == 0
-a[2]/2520 + a[4]/30 - a[6] + 9 a[8] + 90 a[10] == 0
a[1]/362880 - a[3]/1680 + a[5]/24 - (7 a[7])/6 + 10 a[9] + 110 a[11] == 0
a[2]/181440 - a[4]/1260 + a[6]/20 - (4 a[8])/3 + 11 a[10] + 132 a[12] == 0
-a[1]/39916800 + a[3]/120960 - a[5]/1008 + (7 a[7])/120 - (3 a[9])/2 + 12 a[11] + 156 a[13] == 0
-a[2]/19958400 + a[4]/90720 - a[6]/840 + a[8]/15 - (5 a[10])/3 + 13 a[12] + 182 a[14] == 0
a[1]/6227020800 - a[3]/13305600 + a[5]/72576 - a[7]/720 + (3 a[9])/40 - (11 a[11])/6 + 14 a[13] + 210 a[15] == 0
a[2]/3113510400 - a[4]/9979200 + a[6]/60480 - a[8]/630 + a[10]/12 - 2 a[12] + 15 a[14] == 0
-a[1]/1307674368000 + a[3]/2075673600 - a[5]/7983360 + a[7]/51840 - a[9]/560 + (11 a[11])/120 - (13 a[13])/6 + 16 a[15] == 0

Since we need 2 free parameters (since the ODE needs to free parameters to solve,and these are found from the 2 initial conditions),we generate 2 equations less than the number of coeff.It is better to drop equations from the end than from the beginning.

(seriesEqs = seriesEqs[[Range[1, Length[seriesEqs] - 2]]])//TableForm

a[0]+2 a[2]==0
2 a[1]+6 a[3]==0
3 a[2]+12 a[4]==0
-a[1]/6 + 4 a[3] + 20 a[5] == 0
-a[2]/3 + 5 a[4] + 30 a[6] == 0
a[1]/120 - a[3]/2 + 6 a[5] + 42 a[7] == 0
a[2]/60 - (2 a[4])/3 + 7 a[6] + 56 a[8] == 0
-a[1]/5040 + a[3]/40 - (5 a[5])/6 + 8 a[7] + 72 a[9] == 0
-a[2]/2520 + a[4]/30 - a[6] + 9 a[8] + 90 a[10] == 0
a[1]/362880 - a[3]/1680 + a[5]/24 - (7 a[7])/6 + 10 a[9] + 110 a[11] == 0
a[2]/181440 - a[4]/1260 + a[6]/20 - (4 a[8])/3 + 11 a[10] + 132 a[12] == 0
-a[1]/39916800 + a[3]/120960 - a[5]/1008 + (7 a[7])/120 - (3 a[9])/2 + 12 a[11] + 156 a[13] == 0
-a[2]/19958400 + a[4]/90720 - a[6]/840 + a[8]/15 - (5 a[10])/3 + 13 a[12] + 182 a[14] == 0
a[1]/6227020800 - a[3]/13305600 + a[5]/72576 - a[7]/720 + (3 a[9])/40 - (11 a[11])/6 + 14 a[13] + 210 a[15] == 0

Now solve for coeff a[2],a[3],...,a[15]  in terms of a[0] and a[1]

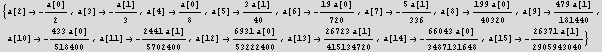
coeff = Flatten[Solve[seriesEqs, Table[a[i], {i, 2, 15}]]]

Now plug these coeff. back into the trial series solution

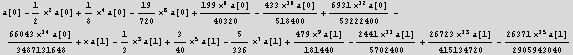
trialSeriesSolution = trialSeriesSolution/.coeff

Collect[trialSeriesSolution, {a[0], a[1]}]

5. Consider the differential equation   x y''[x]+2 y'[x] +4 y[x]= 0
a) find the solution using DSolve

Remove["Global`*"]

odeEquation = x y''[x] + 2 y '[x] + 4 y[x] ;

exactSolution = Flatten[DSolve[odeEquation == 0, y[x], x]]

{y[x] → (BesselJ[1, 4 x^(1/2)] C[1])/(2 x^(1/2)) - ( BesselY[1, 4 x^(1/2)] C[2])/x^(1/2)}

b) Construct power series solutions " by hand" by substituting a trial solution of a generalized power series of the form x^b Underoverscript[∑ , i = 0, arg3]a[i]x^i . Find the indicial equation and find the possible values for the exponent b.

powerSeries = x^bUnderoverscript[∑, i = 0, arg3] a[i] x^i ;

eq = odeEquation/.y→Function[x, Evaluate[powerSeries]]

Divide by x^b and expand in series

tmp = Series[Expand[eq/x^b], {x, 0, 4}]

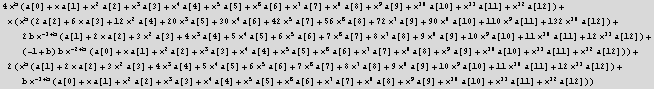
We need to choos value for 'b' to make the coeff. of the lowest powers of x vanish.

indicialEq = tmp[[3, 1]]

b a[0] + b^2 a[0]

Flatten[Solve[indicialEq == 0, b]]

{b→ -1, b→0}

c) Construct the power series solution corresponding to the largest value of b. Carefully consider the number of equations and the number of unknowns you generate. If there are atypical equations at the end , use Drop to get rid of them. You will probably want a free parameter to start the recursion relation.  If you use a free parameter, set it ==1 to get a unique solution.

From part (b) we see that b=0 is the larger of the two solutions of the indicial equation

firstSolutionSeries = powerSeries/.b→0

a[0] + x a[1] + x^2 a[2] + x^3 a[3] + x^4 a[4] + x^5 a[5] + x^6 a[6] + x^7 a[7] + x^8 a[8] + x^9 a[9] + x^10 a[10] + x^11 a[11] + x^12 a[12]

Now plug the above series into the original DE

odeEquation/.y→Function[x, Evaluate[firstSolutionSeries]]//Expand

Generate the equations to solve for the a's

(firstSolutionSeriesEqs = Table[Coefficient[%, x, i] == 0, {i, 0, 12}])//TableForm

4 a[0]+2 a[1]==0
4 a[1]+6 a[2]==0
4 a[2]+12 a[3]==0
4 a[3]+20 a[4]==0
4 a[4]+30 a[5]==0
4 a[5]+42 a[6]==0
4 a[6]+56 a[7]==0
4 a[7]+72 a[8]==0
4 a[8]+90 a[9]==0
4 a[9]+110 a[10]==0
4 a[10]+132 a[11]==0
4 a[11]+156 a[12]==0
4 a[12]==0

we have 13 equations but 12 unknowns. If a[12]==0 this will cause all other coeff to become zero due to chain reaction. So  drop last equation

(firstSolutionSeriesEqs = Drop[firstSolutionSeriesEqs, -1])//TableForm

4 a[0]+2 a[1]==0
4 a[1]+6 a[2]==0
4 a[2]+12 a[3]==0
4 a[3]+20 a[4]==0
4 a[4]+30 a[5]==0
4 a[5]+42 a[6]==0
4 a[6]+56 a[7]==0
4 a[7]+72 a[8]==0
4 a[8]+90 a[9]==0
4 a[9]+110 a[10]==0
4 a[10]+132 a[11]==0
4 a[11]+156 a[12]==0

make a[0] as free parameter. Set it to 1 to solve the equations

(firstSolutionSeriesEqs = firstSolutionSeriesEqs/.a[0] →1)//TableForm

4+2 a[1]==0
4 a[1]+6 a[2]==0
4 a[2]+12 a[3]==0
4 a[3]+20 a[4]==0
4 a[4]+30 a[5]==0
4 a[5]+42 a[6]==0
4 a[6]+56 a[7]==0
4 a[7]+72 a[8]==0
4 a[8]+90 a[9]==0
4 a[9]+110 a[10]==0
4 a[10]+132 a[11]==0
4 a[11]+156 a[12]==0

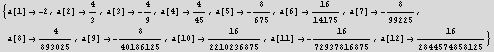
firstSolutionSeriesCoeff = Flatten[Solve[firstSolutionSeriesEqs, Table[a[i], {i, 1, 12}]]]

firstSolutionSeries = firstSolutionSeries/.firstSolutionSeriesCoeff

replace a[0] by 1 since that is what we used as free parameter, and now we obtain sol1 finally

firstSolutionSeries = firstSolutionSeries/.a[0] →1

d) Now construct another another power series solution using a trial solution of the form
sol1 Log[x] +x^b Underoverscript[∑ , i = 0, arg3]a[i]x^i , where sol1 is the solution from part b), and "b" is the indicial exponent you did not use in part b). As in part b), drop anomalous equations at the end of the list. Be particularly careful about choosing which of the a[i] should be considered as variables and which should be considered as free parameters. When you are done, set the free parameter to 1.

b = -1 ;   (*this is the second indicial exponent we did not use*)

secondSolutionSeries = firstSolutionSeries  Log[x] + x^bUnderoverscript[∑, i = 0, arg3] a[i] x^i

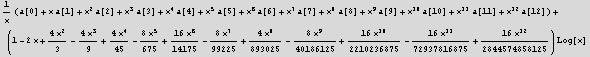
plug into the DE

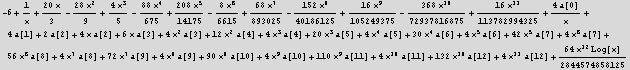
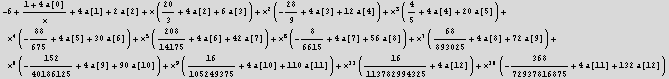
odeEquation/.y→Function[x, Evaluate[secondSolutionSeries]]//Expand

eqs = Series[%, {x, 0, 11}]//Normal

Now set the coeff. of each power of x to zero

(secondSolutionSeriesEqs = Table[Coefficient[%, x, i] == 0, {i, -1, 11}])//TableForm

1+4 a[0]==0
-6+4 a[1]+2 a[2]==0
20/3 + 4 a[2] + 6 a[3] == 0
-28/9 + 4 a[3] + 12 a[4] == 0
4/5 + 4 a[4] + 20 a[5] == 0
-88/675 + 4 a[5] + 30 a[6] == 0
208/14175 + 4 a[6] + 42 a[7] == 0
-8/6615 + 4 a[7] + 56 a[8] == 0
68/893025 + 4 a[8] + 72 a[9] == 0
-152/40186125 + 4 a[9] + 90 a[10] == 0
16/105249375 + 4 a[10] + 110 a[11] == 0
-368/72937816875 + 4 a[11] + 132 a[12] == 0
16/113782994325 + 4 a[12] == 0

Eliminate the last equation

(secondSolutionSeriesEqs = Drop[secondSolutionSeriesEqs, -1])//TableForm

1+4 a[0]==0
-6+4 a[1]+2 a[2]==0
20/3 + 4 a[2] + 6 a[3] == 0
-28/9 + 4 a[3] + 12 a[4] == 0
4/5 + 4 a[4] + 20 a[5] == 0
-88/675 + 4 a[5] + 30 a[6] == 0
208/14175 + 4 a[6] + 42 a[7] == 0
-8/6615 + 4 a[7] + 56 a[8] == 0
68/893025 + 4 a[8] + 72 a[9] == 0
-152/40186125 + 4 a[9] + 90 a[10] == 0
16/105249375 + 4 a[10] + 110 a[11] == 0
-368/72937816875 + 4 a[11] + 132 a[12] == 0

secondSolutionSeriesCoeff = Flatten[Solve[secondSolutionSeriesEqs, Table[a[i], {i, 0, 11}]]]

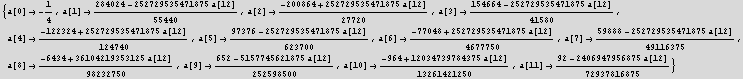
Now set the free parameter to 1 as requested by the problem. From above we see that the free parameter is a[12]

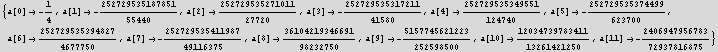
secondSolutionSeriesCoeff = secondSolutionSeriesCoeff/.a[12] →1

and now use these coeff's back in the series itself

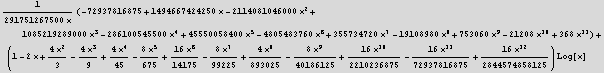
secondSolutionSeries = secondSolutionSeries/.secondSolutionSeriesCoeff ;

secondSolutionSeries = secondSolutionSeries/.a[12] →1//Simplify

Now print solutions. append to the first solution the second solution

firstSolutionSeries

secondSolutionSeries

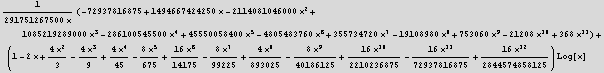
e) Check your results by computing the series using the MathematicaHandbook function frobenius.

<<"MMHTools`DETools`"

{bookSolutionFirstSeries, bookSolutionSecondSeries} = frobenius[odeEquation, y, x, 0, 12, False] ;

bookSolutionFirstSeries

bookSolutionSecondSeries//Simplify

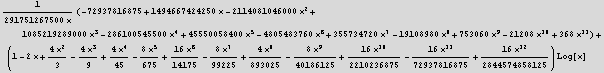
We see they are the same. Verified

f) Now make sure the series solutions you have found are equivalent to some combination of the exact solutions you found in part a). Do this by finding values of C[1] and C[2]  in the exact solution which yield a power series that matches your first and second power series solution. Note: EulerGamma is a constant that is approximately 0.57. Collect is a useful tool to collect the terms proportional to Log[x].

Start by just printing again the solutions I found in part (d)

firstSolutionSeries

secondSolutionSeries//Expand

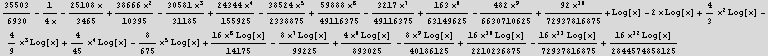
print the exact solution from part (a)

exactSolution = y[x]/.exactSolution

(BesselJ[1, 4 x^(1/2)] C[1])/(2 x^(1/2)) - ( BesselY[1, 4 x^(1/2)] C[2])/x^(1/2)

seriesSolutionFromExactSolution = Series[exactSolution, {x, 0, 12}]

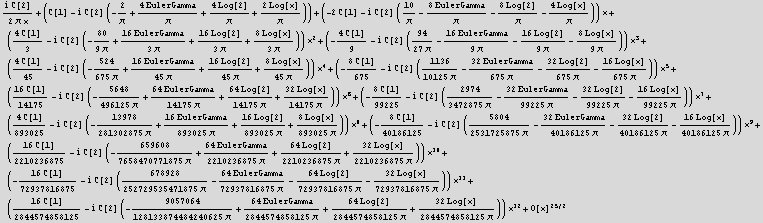
replace EulerGamma by .57

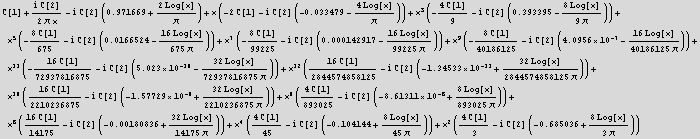
seriesSolutionFromExactSolution = seriesSolutionFromExactSolution/.EulerGamma→.57//Normal

get the terms that are being multiplied by log[x]

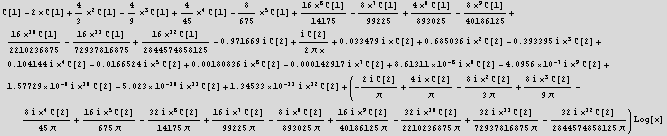
Collect[seriesSolutionFromExactSolution, Log[x]]

CORRECTION:

I solved finding C[1] and C[2] now by inspection.

I Compare the above series solutiuon generated from the exact solution to my series solutions, and looking at the terms that are being multipled by Log[x], I see that (- 2 C[2])/π=1 hence
                             
                                                                                              C[2]=π/(-2)=(π )/2
And by comparing the coeff. with no 'x' in them, I see that

                                                                                              C[1]=1+35503/6930=6.12309
Hence these are the C[1] and C[2] that needs to be used in the exact solution generated by Mathematica DSolve result.

6.  Make a table to show that Bessel functions of half integer order reduce to trigonometric ( or exponential) functions. These are related to the spherical bessel functions which arise from separating the wave equation in 3 dimensions.

First make some plots to show Bessel functions.

Remove["Global`*"] ;

Needs["Graphics`Colors`"]

Plot[Evaluate[Table[BesselJ[n, x], {n, 0, 5}]], {x, 0, 10}, PlotRange->All, AxesLabel→TraditionalForm/@{x, BesselJ[n, x]}, PlotStyle→ {Black, Red, Yellow, Green, Blue, Orange}] ;

[Graphics:HTMLFiles/index_1226.gif]

[Graphics:HTMLFiles/index_1228.gif]

Make table of Bessel functions for half integers side-by-side. We must use odd values of 'n' to get the half part

t = Table[{n, BesselJ[n/2, x], BesselK[n/2, x]}, {n, 1, 10, 2}] ;

TableForm[t, TableHeadings→ {None, {"n", TraditionalForm[BesselJ[n, x]], TraditionalForm[BesselK[n/2, x]]}}]

n J_n(x) K_n/2(x)
1 (2/π^(1/2) Sin[x])/x^(1/2) (^(-x) π/2^(1/2))/x^(1/2)
3 (2/π^(1/2) (-Cos[x] + Sin[x]/x))/x^(1/2) (^(-x) π/2^(1/2) (1 + 1/x))/x^(1/2)
5 (2/π^(1/2) (-(3 Cos[x])/x - Sin[x] + (3 Sin[x])/x^2))/x^(1/2) (^(-x) π/2^(1/2) (1 + 3/x^2 + 3/x))/x^(1/2)
7 (2/π^(1/2) (Cos[x] - (15 Cos[x])/x^2 + (15 Sin[x])/x^3 - (6 Sin[x])/x))/x^(1/2) (^(-x) π/2^(1/2) (1 + 15/x^3 + 15/x^2 + 6/x))/x^(1/2)
9 (2/π^(1/2) (-(105 Cos[x])/x^3 + (10 Cos[x])/x + Sin[x] + (105 Sin[x])/x^4 - (45 Sin[x])/x^2))/x^(1/2) (^(-x) π/2^(1/2) (1 + 105/x^4 + 105/x^3 + 45/x^2 + 10/x))/x^(1/2)

From the above table I see that the J_n function generate trig functions . Also, the BesselK function generate exponential functions for half integers .

7. Relations between special functions and hypergeometric functions.
a)  Make a table for n=1,6 to show that the Legendre functions P_n(1-2x) can be expressed in terms of 2F1[-n,n+1,1,x]. See Mathematical Functions-> Hypergeometric Related in the Help browser for more information on Mathematica's  commands for these functions

Remove["Global`*"] ;

tb = Table[{n, LegendreP[n, 1 - 2 x], Hypergeometric2F1[-n, n + 1, 1, x]}, {n, 1, 6}] ;

TableForm[tb, TableHeadings→ {None, {"n", P (1-2x), "2F1[-n,n+1,1,x]"}}] n

n P (1-2x) n 2F1[-n,n+1,1,x]
1 1-2 x 1-2 x
2 1 - 6 x + 6 x^2 1 - 6 x + 6 x^2
3 1 - 12 x + 30 x^2 - 20 x^3 1 - 12 x + 30 x^2 - 20 x^3
4 1 - 20 x + 90 x^2 - 140 x^3 + 70 x^4 1 - 20 x + 90 x^2 - 140 x^3 + 70 x^4
5 1 - 30 x + 210 x^2 - 560 x^3 + 630 x^4 - 252 x^5 1 - 30 x + 210 x^2 - 560 x^3 + 630 x^4 - 252 x^5
6 1 - 42 x + 420 x^2 - 1680 x^3 + 3150 x^4 - 2772 x^5 + 924 x^6 1 - 42 x + 420 x^2 - 1680 x^3 + 3150 x^4 - 2772 x^5 + 924 x^6

b) Show that the Laguerre polynomials ( important for radial wave functions, often denoted by L_n^m)  can be expressed in terms of the confluent hypergeometric function U[-n, m+1, x]. Find the constant of proportionality.

Compare both functions. First select m=1

m = 1 ;

tb = Table[{n, LaguerreL [n, m, x], HypergeometricU[-n, m + 1, x]}, {n, 1, 6}] ;

TableForm[tb, TableHeadings→ {None, {"n", LaguerreL [n, m, x], "HypergeometricU[-n,m+1,x]"}}]

n LaguerreL [n, m, x] HypergeometricU[-n,m+1,x]
1 2-x -2+x
2 1/2 (6 - 6 x + x^2) 6 - 6 x + x^2
3 1/6 (24 - 36 x + 12 x^2 - x^3) -24 + 36 x - 12 x^2 + x^3
4 1/24 (120 - 240 x + 120 x^2 - 20 x^3 + x^4) 120 - 240 x + 120 x^2 - 20 x^3 + x^4
5 1/120 (720 - 1800 x + 1200 x^2 - 300 x^3 + 30 x^4 - x^5) -720 + 1800 x - 1200 x^2 + 300 x^3 - 30 x^4 + x^5
6 1/720 (5040 - 15120 x + 12600 x^2 - 4200 x^3 + 630 x^4 - 42 x^5 + x^6) 5040 - 15120 x + 12600 x^2 - 4200 x^3 + 630 x^4 - 42 x^5 + x^6

Looking at the above I see that LaguerreL is the same as HyperU but with a factor1/n ! involved .

There is a sign that changes as well . When n is odd, the sign is negative .

When n is even, the sign is positive . So it looks from this one trial that the propertionality is (-1)^n/n !

Lets try for m = 2 to see if this remains the case

m = 2 ;

tb = Table[{n, LaguerreL [n, m, x], HypergeometricU[-n, m + 1, x]}, {n, 1, 6}] ;

TableForm[tb, TableHeadings→ {None, {"n", LaguerreL [n, m, x], "HypergeometricU[-n,m+1,x]"}}]

n LaguerreL [n, m, x] HypergeometricU[-n,m+1,x]
1 3-x -3+x
2 1/2 (12 - 8 x + x^2) 12 - 8 x + x^2
3 1/6 (60 - 60 x + 15 x^2 - x^3) -60 + 60 x - 15 x^2 + x^3
4 1/24 (360 - 480 x + 180 x^2 - 24 x^3 + x^4) 360 - 480 x + 180 x^2 - 24 x^3 + x^4
5 1/120 (2520 - 4200 x + 2100 x^2 - 420 x^3 + 35 x^4 - x^5) -2520 + 4200 x - 2100 x^2 + 420 x^3 - 35 x^4 + x^5
6 1/720 (20160 - 40320 x + 25200 x^2 - 6720 x^3 + 840 x^4 - 48 x^5 + x^6) 20160 - 40320 x + 25200 x^2 - 6720 x^3 + 840 x^4 - 48 x^5 + x^6

It looks so ! Although this is not an exact mathematical proof,   so I conclude that LaguerreL[n, m, x] = (-1)^n/n ! HypergeometricU[-n, m + 1, x]

c) Show that the Hermite polynomials can be expressed as  U[-n/2, 1/2, x^2].

First print few Hermite polynomials to see the form

Table[{n, HermiteH[n, x]}, {n, 0, 10}] ;

TableForm[%, TableHeadings→ {None, {"n", "HermiteH[n,x]"}}]

n HermiteH[n,x]
0 1
1 2 x
2 -2 + 4 x^2
3 -12 x + 8 x^3
4 12 - 48 x^2 + 16 x^4
5 120 x - 160 x^3 + 32 x^5
6 -120 + 720 x^2 - 480 x^4 + 64 x^6
7 -1680 x + 3360 x^3 - 1344 x^5 + 128 x^7
8 1680 - 13440 x^2 + 13440 x^4 - 3584 x^6 + 256 x^8
9 30240 x - 80640 x^3 + 48384 x^5 - 9216 x^7 + 512 x^9
10 -30240 + 302400 x^2 - 403200 x^4 + 161280 x^6 - 23040 x^8 + 1024 x^10

Now show HermiteH side-by-side with U function to see the mapping

t = Table[{n, HermiteH[n, x], HypergeometricU[-n/2, 1/2, x^2]}, {n, 0, 10}] ;

n HermiteH[n,x] -n 1 2 HypergeometricU[ --, -, x ] 2 2
0 1 1
1 2 x x
2 -2 + 4 x^2 -1/2 + x^2
3 4 x (-3 + 2 x^2) -(3 x)/2 + x^3
4 4 (3 - 12 x^2 + 4 x^4) 3/4 - 3 x^2 + x^4
5 8 x (15 - 20 x^2 + 4 x^4) (15 x)/4 - 5 x^3 + x^5
6 8 (-15 + 90 x^2 - 60 x^4 + 8 x^6) 1/8 (-15 + 90 x^2 - 60 x^4 + 8 x^6)
7 16 x (-105 + 210 x^2 - 84 x^4 + 8 x^6) 1/8 x (-105 + 210 x^2 - 84 x^4 + 8 x^6)
8 16 (105 - 840 x^2 + 840 x^4 - 224 x^6 + 16 x^8) 105/16 - (105 x^2)/2 + (105 x^4)/2 - 14 x^6 + x^8
9 32 x (945 - 2520 x^2 + 1512 x^4 - 288 x^6 + 16 x^8) (945 x)/16 - (315 x^3)/2 + (189 x^5)/2 - 18 x^7 + x^9
10 32 (-945 + 9450 x^2 - 12600 x^4 + 5040 x^6 - 720 x^8 + 32 x^10) 1/32 (-945 + 9450 x^2 - 12600 x^4 + 5040 x^6 - 720 x^8 + 32 x^10)

We see that HermiteH[n,x] is just the above HyperU with a constant factor difference.  To find the ratio, divide each HermiteH polynomial by the corresponding Hyper polynomial and look at the pattern. Pull out the polynomials from the above table and divide them

hermite = t[[All, 2]]

hyper = t[[All, 3]]

Simplify[hermite/hyper]

{1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024}

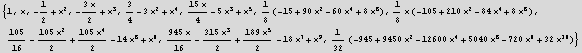
We see from above that HermiteH[n,x] is 2^n times HypergeometricU[-n/2,1/2,x^2]

Lets verify this by regenrate the above table with this factor now added

t = Table[{n, HermiteH[n, x], 2^n  HypergeometricU[-n/2, 1/2, x^2]}, {n, 0, 10}] ;

n HermiteH[n,x] n -n 1 2 2 HypergeometricU[ --, -, x ] 2 2
0 1 1
1 2 x 2 x
2 -2 + 4 x^2 -2 + 4 x^2
3 4 x (-3 + 2 x^2) 4 x (-3 + 2 x^2)
4 4 (3 - 12 x^2 + 4 x^4) 4 (3 - 12 x^2 + 4 x^4)
5 8 x (15 - 20 x^2 + 4 x^4) 8 x (15 - 20 x^2 + 4 x^4)
6 8 (-15 + 90 x^2 - 60 x^4 + 8 x^6) 8 (-15 + 90 x^2 - 60 x^4 + 8 x^6)
7 16 x (-105 + 210 x^2 - 84 x^4 + 8 x^6) 16 x (-105 + 210 x^2 - 84 x^4 + 8 x^6)
8 16 (105 - 840 x^2 + 840 x^4 - 224 x^6 + 16 x^8) 16 (105 - 840 x^2 + 840 x^4 - 224 x^6 + 16 x^8)
9 32 x (945 - 2520 x^2 + 1512 x^4 - 288 x^6 + 16 x^8) 32 x (945 - 2520 x^2 + 1512 x^4 - 288 x^6 + 16 x^8)
10 32 (-945 + 9450 x^2 - 12600 x^4 + 5040 x^6 - 720 x^8 + 32 x^10) 32 (-945 + 9450 x^2 - 12600 x^4 + 5040 x^6 - 720 x^8 + 32 x^10)

We see they are the same.
    

8.  In addition to separation of variables problems in cylindrical coordinates, Bessel functions also show up in a number of Fourier-type integrals.  Show that ∫_ ( 0)^( π)^(  x Cos[t])dt=π J_0[x], first by simply using Integrate, and then by expanding in a series of powers of x  and integrating term by term and comparing to the series for J_0

Remove["Global`*"] ;

integrand = ^( x Cos[t])

^( x Cos[t])

Simplify[∫_0^πintegrand t, Assumptions→Element[x, Reals]]

π BesselJ[0, x]

seriesFirstAnswer = Series[%, {x, 0, 10}]//Normal//Simplify

π (1 - x^2/4 + x^4/64 - x^6/2304 + x^8/147456 - x^10/14745600)

intgrandInSeries = Series[integrand, {x, 0, 10}]//Normal

seriesSecondAnswer = ∫_0^πintgrandInSeries t//Simplify

π (1 - (x^2 (3686400 - 230400 x^2 + 6400 x^4 - 100 x^6 + x^8))/14745600)

seriesFirstAnswer - seriesSecondAnswer//Simplify

0

Created by Mathematica  (January 30, 2007) Valid XHTML 1.1!