Physics 229& 100 Homework #6
Name: Nasser Abbasi
1. Propagation of waves through a thin film in 1 dimension. Waves propagating to the right are represented by ![]() terms and waves propagating to the left are represented by
terms and waves propagating to the left are represented by ![]() terms. k is the magnitude of the wave vector which is
terms. k is the magnitude of the wave vector which is ![]() =
= ![]() , where ω is the angular frequency , and c is the speed of the wave in the external media. Inside the film, the wave speed is slower by a factor of n ( in optics, this is the index of refraction) , so the k vector kf=
, where ω is the angular frequency , and c is the speed of the wave in the external media. Inside the film, the wave speed is slower by a factor of n ( in optics, this is the index of refraction) , so the k vector kf=![]() . ω is determined by the source of the waves and is the same inside and outside the film.
. ω is determined by the source of the waves and is the same inside and outside the film.
![[Graphics:HTMLFiles/index_6.gif]](HTMLFiles/index_6.gif)
a) On the left hand side, the incident wave has unit amplitude, and the reflected wave has amplitude R , so the total field is ![]() + R
+ R ![]() . On the right hand side, there is only the transmitted wave with amplitude T. Inside the film, waves can go both directions so the field is some combination of left and right going waves, as indicated in the figure. The film has thickness d.
. On the right hand side, there is only the transmitted wave with amplitude T. Inside the film, waves can go both directions so the field is some combination of left and right going waves, as indicated in the figure. The film has thickness d.
The reflection and transmission coefficients are determined by the boundary conditions at the interfaces of the film, which are that the field amplitude is continuous and the derivative of the field is continuous; the same type of logic holds for acoustic waves, light waves, and quantum waves. Calculate the amplitude transmission coefficient T in terms of k, kf and d.
![]()
![]()
![]()
![]()
Now set the 4 equations using the boundary conditions given
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
So we have now 4 equations, here they are
![]()
| 1+R==A+B |
Now I need to solve the above to find T
![]()
![]()
![]()
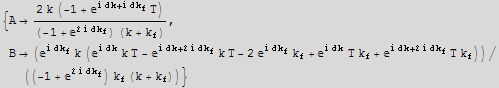
![]()
![]()
![]()
![]()
![]()
b) T is the amplitude transmission coefficient; the intensity of the transmitted wave or the probability of transmission is measured by the energy transmission coefficient TE= T T*. Find a compact expression for this quantity in terms of k, kf and d.
![]()
![]()
c) The k vector inside the film kf is related to the k vector in the external media by kf=n k, where n is the optical index, or the ratio of the wave speeds. Express TE in terms of k , d and n.
![]()
![]()
c) TE and n are dimensionless ratios. The only terms in the above expression that have dimensions are k and d, but they appear in the dimensionless combination k d = ![]() . Let d→dr λ , where dr is a "reduced" film thickness measured in units of the wavelength, and express TE in terms of n and dr
. Let d→dr λ , where dr is a "reduced" film thickness measured in units of the wavelength, and express TE in terms of n and dr
![]()
![]()
![]()
d) Let n→1.5 ( typical for glass) and make a plot as a function of dr. Where do the maxima and minima occur? Comment on the physical significance of the plot.
![]()
![]()
![]()
![[Graphics:HTMLFiles/index_45.gif]](HTMLFiles/index_45.gif)
![]()
2. Using the discussion of polar coordinates as a guide, compute the expression for the laplacian in spherical coordinates. This will require expressing , for example, ![]() =
= ![]()
![]() +
+![]()
![]() +
+![]()
![]() . Use makeop to make a ddx operator . Compare your answer with the expression obtained from the VectorAnalysis package using Laplacian.
. Use makeop to make a ddx operator . Compare your answer with the expression obtained from the VectorAnalysis package using Laplacian.
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()

Now each row in the inverse of the transpose of the jacobian matrix represent partial derivative of x or y or z w.r.t. to the spherical coordinates. Use makeop to make partial operators as follows
![]()
![]()
![]()
Now that we have have constructued the first partial derivatives operators, we apply the operator again to obtain the second partial derivatives, and then add them to make the Laplacian
![myAnswer = ddxop[ddxop[g[r, θ, φ]]] + ddyop[ddyop[g[r, θ, φ]]] + ddzop[ddzop[g[r, θ, φ]]]//Simplify ;](HTMLFiles/index_67.gif)
![]()
![]()
Now find the Laplacian in spherical using Mathematica and then compare the answers
![]()
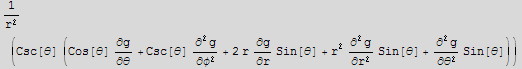
![]()
![]()
The above verifies the answer is the same.
3. Construct the matrix which maps the components of a Cartesian vector into the components of a vector in Spherical coordinates. Use JacobianMatrix and ScaleFactors from the VectorAnalysis package. Use the mapping to convert the Cartesian vector ![]() = {0,0,1} into spherical coordinates.
= {0,0,1} into spherical coordinates.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Now Verify above answer using Mathematica
![]()
![]()
4 a) In Spherical coordinates, calculate ![]() (
( ![]() ), and
), and ![]() (
( ![]()
![]() (θ,φ)) (see SphericalHarmonicY in Help).
(θ,φ)) (see SphericalHarmonicY in Help).
![]()
![]()
![]()
![]()
![]()
![]()
![]()
b) In Spherical coordinates, calculate ∇·(![]()
![]() ) , where
) , where ![]() is the unit vector in the r direction.
is the unit vector in the r direction.
![]()
![]()
![]()
![]()
![]()
![]()
c) In Cylindrical coordinates, calculate ∇×![]() , where
, where ![]() is the unit vector in the φ direction.
is the unit vector in the φ direction.
![]()
![]()
![]()
![]()
5. Prove that the shortest path between 2 points in the plane is a straight line. The length of a curve defined by y[x] is ∫ ![]() dx . Find the (2nd order) differential equation that determines the minimum value of the integral. Solve it and show that it represents a line. Also set each of the conserved quantities to a constant, and show that the solution of the resulting (1st order) differential equation also gives a straight line.
dx . Find the (2nd order) differential equation that determines the minimum value of the integral. Solve it and show that it represents a line. Also set each of the conserved quantities to a constant, and show that the solution of the resulting (1st order) differential equation also gives a straight line.
![]()
![]()
Write Euler equation which is ![]() (
(![]() )-
)-![]()
![]()
![]()
![]()
![]()
We see from the above that the solution is a stright line.
![]()
![]()
![]()
Since ![]() =0, then this means
=0, then this means ![]() (
(![]() )=0 or in otherwords,
)=0 or in otherwords, ![]() is constant, say k. hence conserved.
is constant, say k. hence conserved.
We solve this first order ODE
![]()
![]()
![]()
![]()
Hence we see from the above that the solution y(x) also gives straight line

![]()
![]()
![]()
![]()
We see the the solution also gives a stright line.
Hence we have 2 conserved quantities, and each generate first order ODE and each give solution as constant line.
6. A mechanics problem that is found in most text books is the double pendulum, i.e. 2 massless rods of lengths L1 and L2 with masses m1 and m2 at the lower ends arranged so that L1 is attached from the ceiling and L2 is attached at the end of L1. Their positions are described in terms of angular deviation from the vertical of each rod, θ1[t] and θ2[t].
a) Draw a picture of this situation, including the relevant variables, and insert the drawing into this notebook. PowerPoint is probably the easiest to use; PowerPoint drawings can be simply copied and pasted into Mathematica. Any other drawing program can be used, but you will have to convert vector graphics to bitmaps. Alt PrintScreen will make a bitmap image of the monitor which can be edited and cropped in Paint. ![[Graphics:HTMLFiles/index_143.gif]](HTMLFiles/index_143.gif)
b) Assume the double pendulum moves in a plane. Explicitly write the 2D position vectors p1 and p2 of the two masses. Find the velocity vectors v1 and v2. Find expressions for the kinetic energy KE and the gravitational potential energy PE.
![]()
First write the coordinates of each bob
![]()
![]()
![]()
![]()
Now write the vectors for each mass position
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![1/2 (L1^2 (m1 + m2) θ1^′[t]^2 + 2 L1 L2 m2 Cos[θ1[t] - θ2[t]] θ1^′[t] θ2^′[t] + L2^2 m2 θ2^′[t]^2)](HTMLFiles/index_158.gif)
![]()
![]()
PE is not right
![]()
![]()
c) Write the Lagrangian and construct the equations of motion.
![]()
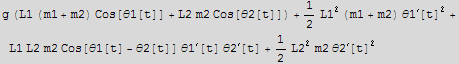
To find equation of motion, I can use Mathematica EulerEquations function
![]()
![]()
![]()
![]()
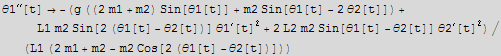 |
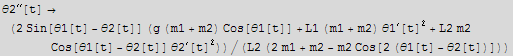 |
7. Symmetric and antisymmetric matrices can be diagonalized, i.e. if M is a symmetric matrix, there exists a matrix C such that for M= RandomSymMat[n_], C M ![]() =diagonal.
=diagonal.![]() is the transpose of C. The rows of C are the normalized eigenvectors of M. This transformation amounts to a change in basis. The fact that diagonal matrices are easy to exponentiate provides another way to exponentiate symmetric matrices. Exp[M t]=
is the transpose of C. The rows of C are the normalized eigenvectors of M. This transformation amounts to a change in basis. The fact that diagonal matrices are easy to exponentiate provides another way to exponentiate symmetric matrices. Exp[M t]=![]() [diag] C, where the diagonal elements of diag are {
[diag] C, where the diagonal elements of diag are { ![]() ,
,![]() ,..}, where
,..}, where ![]() are the eigenvalues of M.
are the eigenvalues of M.
a) Write a function RandomSymmetricMatrix[n_] which returns a random symmetric n x n matrix.
![]()
![]()
![randomSymMat[n_] := Module[{m}, m = UpperDiagonalMatrix[Random[] &, n] ; m = m + Transpose[m] ] ;](HTMLFiles/index_179.gif)
Test the above on small matrix
![]()
![]()
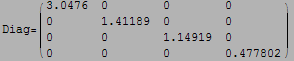
b) Write a function Diag[mat_] that computes C and prints it in MatrixForm and returns the diagonal matrix C M ![]() . Use Dimensions if you need to know how big mat is. Remember that the Mathematica Eigensystems command does not return normalized eigenvectors. You also may want to use N to get your results in decimal form and Chop to get rid of round off trash. Test your function on several matrices generated by RandomSymmetricMatrix.
. Use Dimensions if you need to know how big mat is. Remember that the Mathematica Eigensystems command does not return normalized eigenvectors. You also may want to use N to get your results in decimal form and Chop to get rid of round off trash. Test your function on several matrices generated by RandomSymmetricMatrix.
Notice: Mathematica eigenvectors returned seem to be normalized allready.

Test the function few times
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
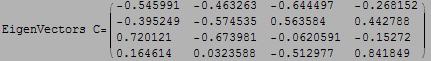
c) Write a function that computes Exp[M t]=![]() [diag] C. Show that it gives the same result as the MatrixExp command for a random symmetric matrix. Make sure your answer contains the variable t.
[diag] C. Show that it gives the same result as the MatrixExp command for a random symmetric matrix. Make sure your answer contains the variable t.
![myMatrixExp[mat_, var_] := Module[{c, diag, λ}, {λ, c} = Eigensystem[mat] ; diag = DiagonalMatrix[^(λ var)] ; Transpose[c] . diag . c]](HTMLFiles/index_195.gif)
![]()
![]()
![]()

![]()

The result is the same.
8. Chemical mixing problem ( from Robertson). Tank A and tank B are connected by a series of pipes. At time t=0, the flow rates shown in the figure are established. The volume of each tank is as shown. Each tank also contains an initial mass of salt, mA0, and mB0. Note that the flow rates into and out of each tank are the same, so the volume of liquid in each tank is fixed, but the salt concentration varies with time.
concentration varies with time. ![[Graphics:HTMLFiles/index_202.gif]](HTMLFiles/index_202.gif)
a) Denote the mass of salt in each tank as mA[t], mB[t], respectively. Write the system of differential equations which describe the rates of change of these quantities.
![]()
![]()
![]()
![]()
![]()
Now for each tank, write the rate of the salt concentration in and out
![(*tank A*)rateIn = r3 mB[t]/Vb ; (*notice, pure water has zero salt concentration, so not part of equation*)rateOut = r4 mA[t]/Va + r2 mA[t]/Va ; eq1 = mA '[t] == rateIn - rateOut](HTMLFiles/index_208.gif)
![]()
![(*tank B*)rateIn = r4 mA[t]/Va ; rateOut = r3 mB[t]/Vb + r1 mB[t]/Vb ; eq2 = mB '[t] == rateIn - rateOut](HTMLFiles/index_210.gif)
![]()
b)Find the general solution using MatrixExp.
![]()
![]()
![]()
![]()
![]()
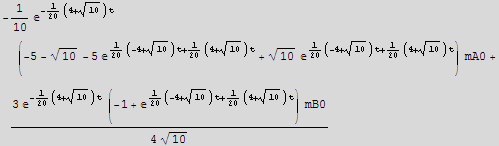
![]()
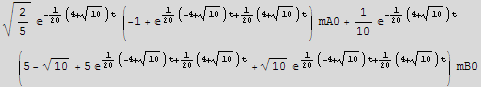
c) use the solution obtained above to find the specific solution for the case mA0=1000, mB0=0. Plot mA[t] and mB[t] on the same plot.
![]()

![[Graphics:HTMLFiles/index_222.gif]](HTMLFiles/index_222.gif)
d) One of the useful features of the MatrixExp approach is that the same solution can be used for different initial conditions. Repeat the above for mA0=0, mB0=1000
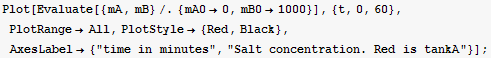
![[Graphics:HTMLFiles/index_224.gif]](HTMLFiles/index_224.gif)
9. A standard representation for the delta function is
δ(x-a)=![]()
![]()
![]()
![]() dt
dt
Evaluate the integral for L=3, 10, 30. Convince yourself that the answer is real, and that the area under all the curves is 1. Plot all three results on a single plot. Set a->1 and plot from {-1,2}. Conclude that the formula is in fact reasonable.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
We see that for real 'a' and 'x', the answer is real and not complex. To show that the area under the curves is 1, we integrate.
![]()
![]()
![]()
![]()

![[Graphics:HTMLFiles/index_242.gif]](HTMLFiles/index_242.gif)
10. (grads) Consider a string whose displacement y[x,t] is a function of x and t. The density of the string is ρ[x]. Let T be the tension in the string, which is constant and provided by a mass .
![[Graphics:HTMLFiles/index_243.gif]](HTMLFiles/index_243.gif)
a) What is the density of kinetic energy, i.e. what function would you integrate over the length of the string to get its total kinetic energy?
b) What is the density of potential energy? A good way to think of this is to consider the constant tension supplied by a mass m hanging over a pulley. Assume that the mass of the string is negligible compared to m.
c) What is the Lagrangian density, and the equations of motion. Show that if the slope of the string is small, the equation is a wave equation. Use DForm to make it look like conventional mathematics.
| Created by Mathematica (January 30, 2007) |