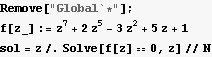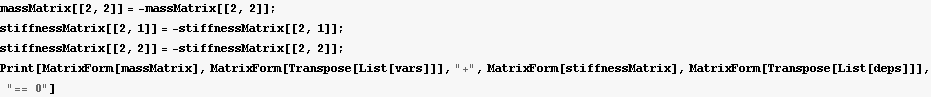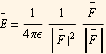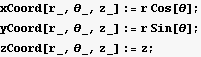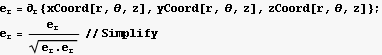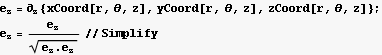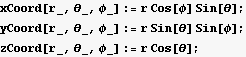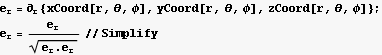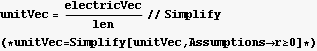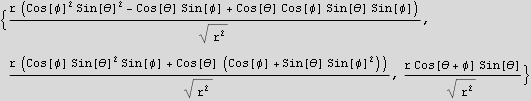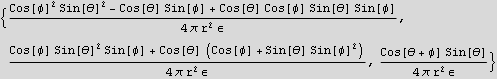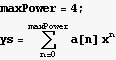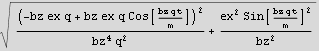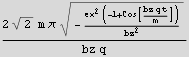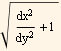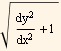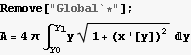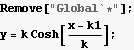Physics 229& 100 Final Exam 2006
Due Tuesday, Dec 12 at noon
Open book, but no discussion with anyone except me. You may use any packages that seem helpful. Provide clear commentary so that I can follow your reasoning.
grads do all problems
undergrads do 1-13 ( 14&15 are extra credit if you do them )
Name: Nasser Abbasi
1. Find a set of vectors that span the hyperplane w - 2.3 x- 2 y- 3.4z==6
Solution outline:
First find a normal to the hyperplane.
Use the fact that given a general equation of a hyperplane when written in the form
Then a normal is just the vector 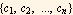 . For example, given the equation of a line, written in the above form, it is a x+b y=c Hence a normal to this line is the vector {a,b}.
. For example, given the equation of a line, written in the above form, it is a x+b y=c Hence a normal to this line is the vector {a,b}.
Once the normal is found, then we can obtain basis for the null space of this normal. The nullspace of this normal gives us the basis vectors which span the space that this normal can not reach.
But the space that this normal vector can not reach is the hyperplane itself.
Hence all what we need to do is to use NullSpace on a Matrix which contains one row, which is the normal vector.
step 1. Find the normal vector:
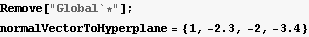
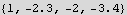
Step 2. Find the NullSpace:
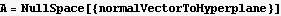
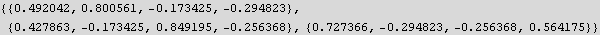
2. Find the solution to the equations
2x+3y+2z=10
5x-2y+7z=0
which has minimum length.
Solution outline:
Write the system as Ax=b and use PseudoInverse to find the minimum solution

Convert equations to matrix form

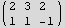
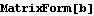
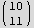
And now use PseudoInverse to find the minimum solution

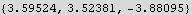
The above is the solution which gives the minimum length which is
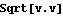
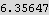
3. Calculate 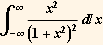 using residues. Show that it is the real part of a complex integral . Specify the contour you are using by drawing a sketch. Explain your reasoning. Check your answer using Integrate.
using residues. Show that it is the real part of a complex integral . Specify the contour you are using by drawing a sketch. Explain your reasoning. Check your answer using Integrate.
Solution outline:
Find the poles of the function that we are integrating. (the integrand in the above). Then Find a laurent series expanded around this pole, and find the coeff. of the term 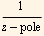 . This is the residue. The solution is then, by the residue theorem, is the sum of all the residues * 2πi. In this problem there is one pole, hence one residue is found.
. This is the residue. The solution is then, by the residue theorem, is the sum of all the residues * 2πi. In this problem there is one pole, hence one residue is found.
Step 1. Start by finding the pole of the integrand

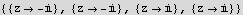
Step 2. I need to consider only poles that are inside the contour, which will be in the upper half plan. Hence there are pole are z=I of order 2. Find Laurent series around the pole, and pick up the coefficient of the term 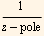
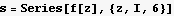
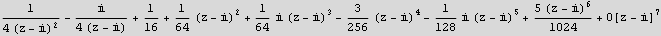
step3 . Now find the correct coeff.

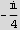
Step 4. Now use the residue theorem to find the value of the integral
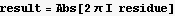
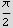
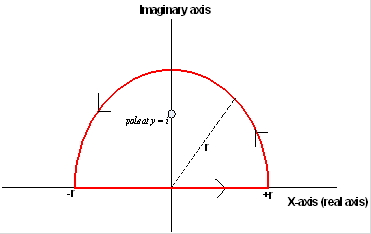
Now I need to show it is the real part of a complex integral. To do this I consider an integral of 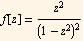 and write the integral as a contour integral that extends over the real x axis from -r to +r and then goes anticlock wise in a circle of radius r from θ=0 to θ=π as shown in this diagram
and write the integral as a contour integral that extends over the real x axis from -r to +r and then goes anticlock wise in a circle of radius r from θ=0 to θ=π as shown in this diagram
Now since  then
then 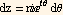 and so the contour integral can be written as
and so the contour integral can be written as
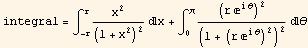
Now since we want to integrate from x=-∞ to x=∞, then we start by making r larger and larger.
Then we can take r to go to infinity. But notice in the second integral above, in the denominator, r is to the power of 4, while in the numerator r is to the power of 2.
Hence the second integral above (the integral over the circular part) will vanish as r becomes larger and larger.
Hence the integral becomes the real part only which is what we are asked to evaluate which is
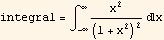
Hence we showed that 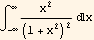 is the real part of contour complex integral
is the real part of contour complex integral 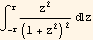 where z is a complex variable
where z is a complex variable 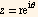
Now I check my answer using Integrate
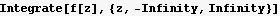
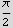
The above matches the result using residue method as shown above.
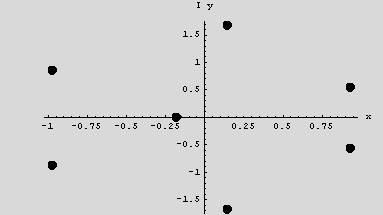
4. Find all solutions to 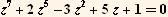 Make a plot which shows the location of the roots in the complex plane.
Make a plot which shows the location of the roots in the complex plane.
Solution outline:
Since this is a polynomial, we can use Solve. Since this is a polynomial of degree 7, this by the fundamental theory of algebra, we will have 7 roots. Use the command ListPlot to make a plot of the roots in the complex plane.
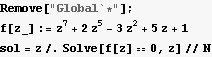
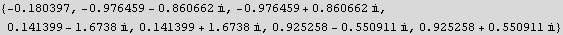
5. Find the 4 smallest positive real roots of 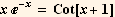
Solution outline:
Make a plot (try different ranges until you see one which contains at least 4 real roots). Then use FindRoot to locate exact roots.
Find make a plot to see the shape
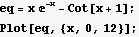
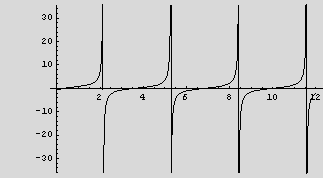
Now by looking at the above plot, I see the smallest 4 positive real roots around 0,4,6,10. So I can use FindRoot with an initial guess at these values. Since my starting guess values are all real, then FindRoot will only find real roots. I also supply a max/min brackets for the range of search by FindRoot for each call.

Hence the 4 smallest positive roots are
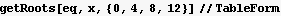
| 0.335409 |
| 3.61542 |
| 6.8467 |
| 13.1371 |
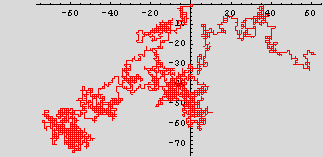
6. A drunken sailor (or a molecule adsorbed on a surface, or a polymer chain) takes a step of unit length in either the +x,-x,+y, or -y directions every unit of time. Write a procedure which will draw a typical trajectory of nstep steps. Use a Do loop, AppendTo, Random[Integer] and ListPlot with the PlotJoined and AspectRatio-> Automatic option. Draw a trajectory of 2000 steps.
Solution outline:
Make an empty list. Generate random integer from 1 to 4. depending on the value make the appropriate step which will be an new entry, add it to the list. At the end use ListPlot to display it.
Declare data and do initialization
Start the main loop.

7. Two identical masses are attached to three springs between two fixed walls, as shown in the figure below. The spring constant of the middle spring is different from the outside springs. Neglect gravity.
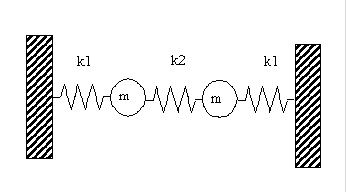
Solution Outline:
Generate the lagrangian, then the equation of motion, from this we find the mass matrix and the stiffness matrix. Solve Det([k]-w^2 [M])=0 to find the eigenfrequencies.
First Update the above diagram as shown below to make it clear where displacement are
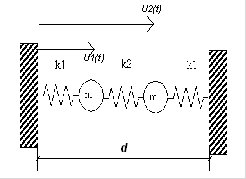
a) Construct the Lagrangian , and set up the equations of motion for this system
Set up symbols using notation for ease of reading.

Now define the kinetic energy KE and the potential energy PE
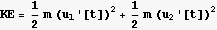
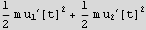
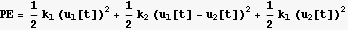
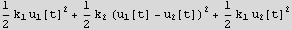
Find the lagrangian L
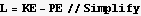
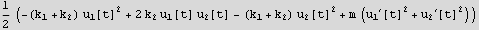
Here I can use EulerEquations[] in ["Calculus`VariationalMethods`"] to get the equations, or do it by hand. This is easy enough so I just write it down from the definition (this way I also do not forget it)
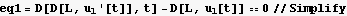
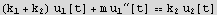
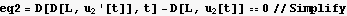
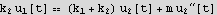
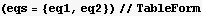
I can also display the above EQM is a more standard format as follows (even though this is not needed to proceed)

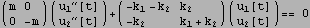
Multiply the LHS and RHS of the second equation above by minus sign to make the mass matrix all positive. Mathematica does not do it automatically. Notice there is a "-m" in the mass matrix above, so the code below just rewrite the above so that the mass matrix is all positive.
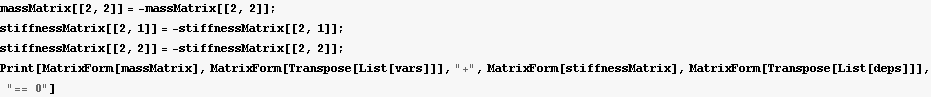
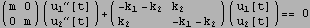
b) Calculate the normal mode frequencies for the vibrations of this system.
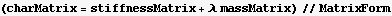
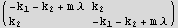

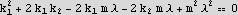
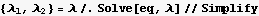
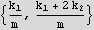
Finally find the harmonic frequencies. Take the positive square root of the above solutions
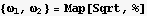

8. a) The unit sphere and a cylinder defined by 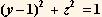 intersect. The region which is inside both the cylinder and the sphere is a peculiar shape. Use ContourPlot3D and RealTime3D to draw a picture of the region which can be rotated so that the region can be examined.
intersect. The region which is inside both the cylinder and the sphere is a peculiar shape. Use ContourPlot3D and RealTime3D to draw a picture of the region which can be rotated so that the region can be examined.
Solution outline:
Divide the volume that is common between the cylinder and the sphere into 2 parts. One is a standard volume shape (dome type shape) with a standard formula for its volume. The second volume, use volume integration to find.



b) What is the volume of this region?
IMPORTRANT:
Since I am not sure if my analytical solution is correct below, I just thought that I could have solved this problem much more easily numerically.
I am not sure if we have to use analytical solution only. But I give this solution below, I get 40% as the covered volume which looks more closer to what I see in the plot. With the analytical solution I get 45%, and I think I over integrated there. So please accept this numerical solution below unless an analytical solution is needed in which case please accept my analytical solution below it. Thank you.
Use MonteCarlo method.
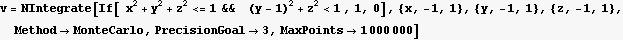
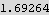
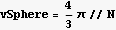
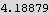
Hence the percentage of the volume found to that of the sphere is
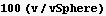
Analytical solution (In case the above is not acceptable)
First find the curve where the cylinder and the sphere meet
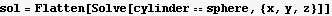
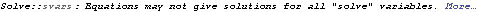
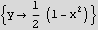
Now find y for x=0
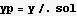
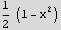
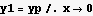
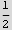
Now the above says y=.5 where the cylinder meets the sphere. Find the z coordinates where this happens

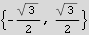
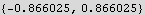
Hence y=0.5 is where the intersection started. That is, if I draw a flat surface at y=.5 that is perpendicular to the y-axis, it will meet the cylinder just as it entered the sphere, like this
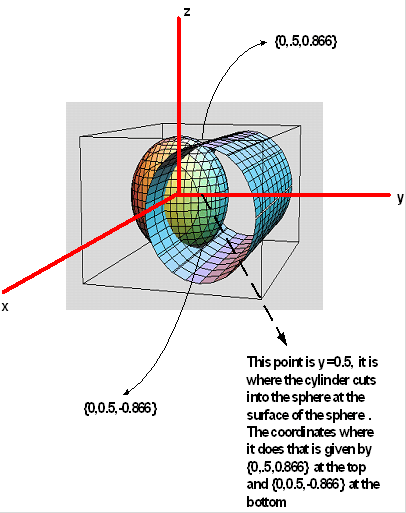
Now imagine a flat surface y=.5 that cuts the sphere, then I have 2 volumes to calculate, one above this surface and one below it as shown. The top surface has a known formula for it which I show below. The bottom surface I calculate using integration as will be done below
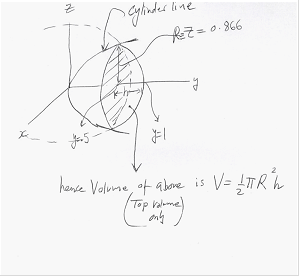
Now I need to find the volume of the segment below the cut-off plane.
A section of the area is given by 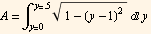 Hence the volume is
Hence the volume is 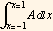 , next multiply this by 2 since it goes around all the way
, next multiply this by 2 since it goes around all the way
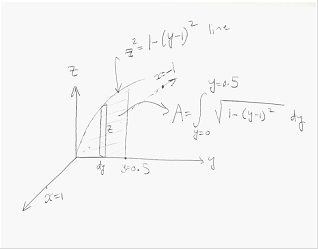

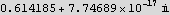
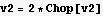
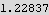

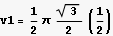
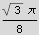
Hence total volume is
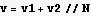
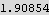
Note the volume of the unit sphere is
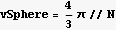
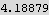
Hence the percentage of the volume found to that of the sphere is
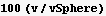
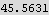
The above is just a little less than half the sphere volume.
9. Express the electric field of a point charge at the origin using cartesian , cylindrical and spherical coordinates and basis vectors. The JacobianMatrix, Scalefactors, and CoordinatesToCartesian functions from the VectorAnalysis package may be useful.
Solution outline:
The electric field is the electric field force per unit charge
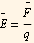
where
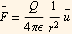
where 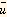 is a unit vector along the direction of the electric force vector
is a unit vector along the direction of the electric force vector 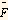
Since we are using a unit charge, and use a unit test charge as well, then
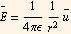
But 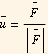 and r is the length of
and r is the length of 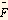 hence
hence
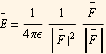
So the problem is 2 parts: Express a vector  in different coordinates systems, and express the length of this vector in different coordinates systems.
in different coordinates systems, and express the length of this vector in different coordinates systems.
step1. Start by creating some symbols
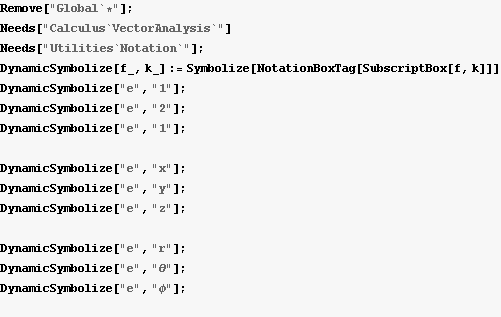
Define a function which takes general vector of the form 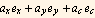 where the a's are coordinates and the e's are the base vectors associates with these coordinates. For example in Cartesians, the vector is
where the a's are coordinates and the e's are the base vectors associates with these coordinates. For example in Cartesians, the vector is 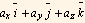 then this function will return its length
then this function will return its length

In Cartesian

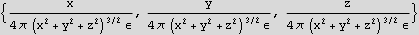

Now in cylindrical
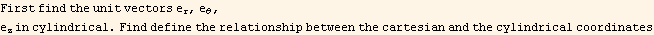
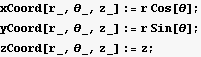
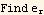
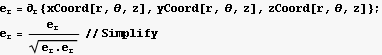
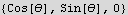
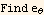

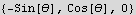
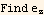
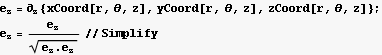
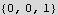
Hence the electric field vector in cylindrical is
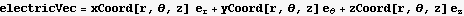
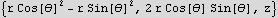
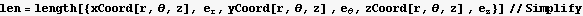
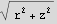

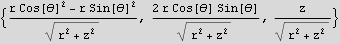
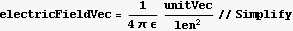
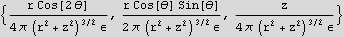
Now do the same for the spherical coordinates. First define the relationship between the cartesian and the spherical coordinates
Now find the unit vectors in spherical coordinates
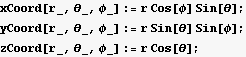
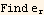
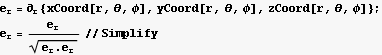
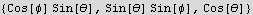
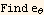
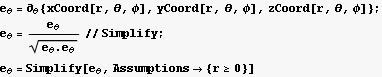
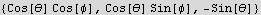
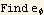

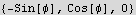
Hence the electric field vector in spherical is
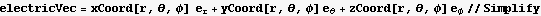
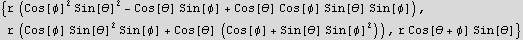
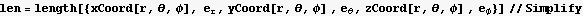
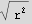
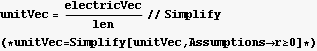
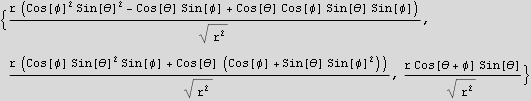

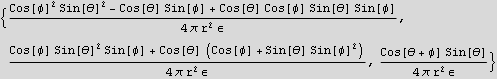
10. Data for the counts recorded in a radioactive decay experiment, in the form {time, counts/min} can be found in a file called decay.dat, which is in the localdata directory defined by

Import the data into a list. The counter registers a background count rate even if there are no decays in the sample. The isotope has a decay constant of -0.3 , so a model for the count rate at time t is A +B 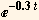 , where A is the background count rate. Find A and B using Fit. Plot the data and the best fit function on the same plot using two different colors.
, where A is the background count rate. Find A and B using Fit. Plot the data and the best fit function on the same plot using two different colors.


Fit the data
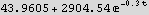
Find A and B
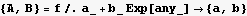
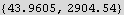
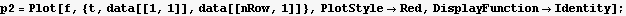
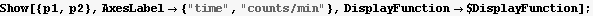
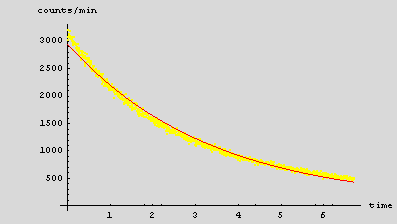
11. Consider the eigenvalue boundary value problem
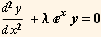 y[0]=0, y[1]=0
y[0]=0, y[1]=0
Find the first 3 eigenvalues and plot the corresponding solutions.
Solution outline: Since this is both an eigenvalue problem and a boundary value problem, DSolve nor NDSolve can solve it as is. Start by converting the problem to an initial value problem. Use y'[0]==1 since it does not matter which initial value for the "speed" we select, we might as well select y'[0]=1.
Next, try a range of eigenvalues, for each use NDSolve to find the solution and evaluate the solution at y[1]. Plot y[1] as a function of λ. Now use FindRoot to find where y[1] is zero on this plot. This gives us the values of λ which when used in the original ODE will result in the correct boundary condition met.

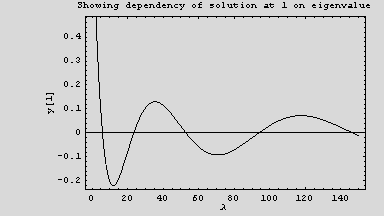
Now by inspection and using FindRoot we find the 4 smallest eigenvalues
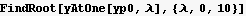
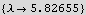

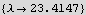

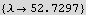
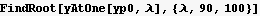
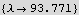
12. For what values of λ does the DE x y''[x] +(1-x) y'[x] +λ y[x]=0 have polynomial solutions?
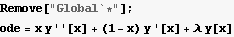
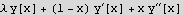
Solution outline:
Assume the solution is a power series. Substitute this solution in the ODE. We find that we get one possible solution with one free parameter, say a[0].
Now look at the series in x which goes with this free parameter a[0].
This series will have λ in it as well.
We want to look at the conditions on λ which makes this series TERMINATE.
This indicates a convergent solution. Using this condition, we can see for what values λ must have to terminate the a[0] series. Hence these will be the λ values which gives a polynomial solution in x.
step 1: Assume a power series solution
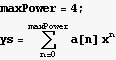
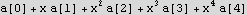
Plug in the ODE

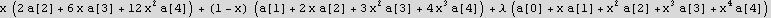
Now since the ODE=0, then each power of x must be zero as well for this to happen. Use this to generate a set of equations
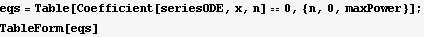
| λ a[0]+a[1]==0 |
| -a[1]+λ a[1]+4 a[2]==0 |
| -2 a[2]+λ a[2]+9 a[3]==0 |
| -3 a[3]+λ a[3]+16 a[4]==0 |
| -4 a[4]+λ a[4]==0 |
Drop the last equation since incomplete due to the side-effect of using series
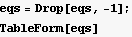
| λ a[0]+a[1]==0 |
| -a[1]+λ a[1]+4 a[2]==0 |
| -2 a[2]+λ a[2]+9 a[3]==0 |
| -3 a[3]+λ a[3]+16 a[4]==0 |
We see from the above that if we solve for a[1] in terms of a[0], then we can solve for a[2] in terms of a[1], and then solve for a[3] in terms of a[2], etc... Hence we use a[0] as a free parameter.
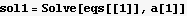
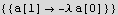
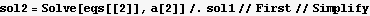
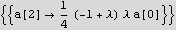
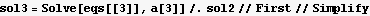
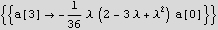
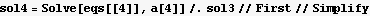
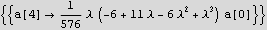
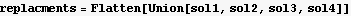
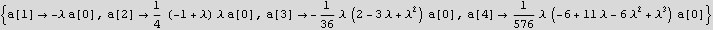
Now plug in all the above into the power series trial solution
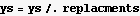
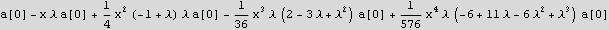
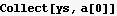
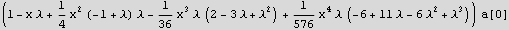
To make it a little easier, let me just remove the a[0] term out of the way for now
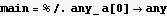
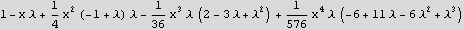
So now, the above is my main object to examine. I need the above series in x to TERMINATE. Here I am only looking at 4 terms because that is what I tried, but more terms can be added. But these are enough to see the pattern.The point is that we want to find the conditions which causes this series to terminate. Use collect to see it better

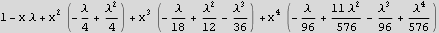
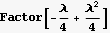
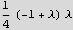
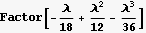
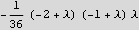
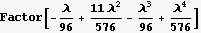
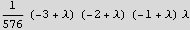
Ok, the pattern is clear now.
From the above we see the following. If λ=1, then that will remove the 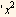 ' term due to the (-1+λ) factor , and it will also remove all the terms in higher power of x after that, since we see that there is a factor (-1+λ) in each term after that. Hence λ=1 is a good eigenvalue in that it gives us a terminating series in x.
' term due to the (-1+λ) factor , and it will also remove all the terms in higher power of x after that, since we see that there is a factor (-1+λ) in each term after that. Hence λ=1 is a good eigenvalue in that it gives us a terminating series in x.
For λ=2, see the same pattern results. It will make the 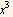 term vanish due it having a (-2+λ) in it. And all higher terms will all vanish as well since each of them has a (-2+λ) factor.
term vanish due it having a (-2+λ) in it. And all higher terms will all vanish as well since each of them has a (-2+λ) factor.
Hence we see that only for λ an integer will the series terminate, giving a polynomial solution. We continue this way.
So for λ=0, the solution is 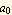 (1)
(1)
So for λ=1, the solution is 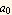 (1-x)
(1-x)
For λ=2, the solution is 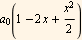
For λ=3, the solution is
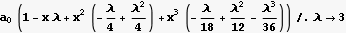
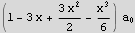
Etc.....
Let 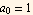 (since free parameter), I get
(since free parameter), I get
So for λ=0, the solution is 1
So for λ=1, the solution is (1-x)
For λ=2, the solution is 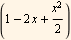
For λ=3, the solution is 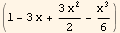
This completes the solution. Hence only for
λ=0,1,2,....
will we get a polynomial solution in x. (for λ=0 it is a constant solution=1).
Note that we rejected non-integer λ values since these will not terminate the series. Also negative λ will not terminate the series.
Btw, it is possible to first see what type of power series solution for this ODE one can expect. The above ODE can be written in the form
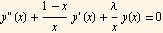
Now look at the functions that go with each coef. above. We see the coefficients functions are: 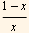 ,
, and these are clearly not analytic at x=0, they blow up. Hence a series solution around x=0 can not be ordinary. It can be only regular singular or irregular singular.
and these are clearly not analytic at x=0, they blow up. Hence a series solution around x=0 can not be ordinary. It can be only regular singular or irregular singular.
If we multiply each coeff. function by (x-x0) or by x since we are expanding around x0=0, then we can remove all of the poles.
Hence all of the coeff. functions become analytic.
Hence the series solution is considered a regular singular.
By Frobenius theorem, for a regular singular point, it guarantees the existence of a least one (or possible two) solutions of the form  where
where 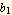 not necessarily integer. This is the solution found above.
not necessarily integer. This is the solution found above.
In addition it says, if there is only one solution of this form, the second solution must be of the form  where
where 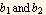 are roots to a quadratic equation called the indicial equation. I do not need to consider this second case, since the first solution
are roots to a quadratic equation called the indicial equation. I do not need to consider this second case, since the first solution 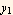 gives us the conditions on λ we are asked to find.
gives us the conditions on λ we are asked to find.
13. The force on a particle with charge q and mass m is given by the familiar formula F=q(E+v×B). Consider the case of a particle of mass m and charge q starting from rest at the origin in a region of space with a constant B field in the z direction and a constant E field in the x direction.
a) Use dimensional analysis to determine the characteristic length, time and energy in this problem.

Now start doing dimensional analysis to find the length scale of the problem (distance from the origin at some future time t). i.e. we are asking the question:
What does the distance away from the origin that the particle will be some time t depends on?
This distance must depend on how strong the magnetic field B is, and on how strong E is, and on the mass of the particle, and on the amount of electric charge on the particle, and on the velocity of the particle. Hence we write
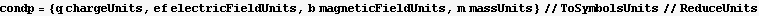
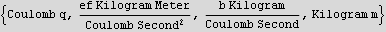
What possible combination can give us a length variable out of the above parameters? use dimanal[]

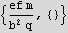
Verify the above answer
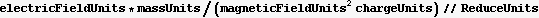
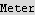
Hence the length scale is given by
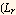 )
)
where 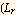 ) is a constant (non-dimensional factor) i.e
) is a constant (non-dimensional factor) i.e
length ~ 
To find what is the length is proportional to, I need to use some physical values. Assume the particle is an electron, we know the mass m and the charge q. For E and B,
Now find a characteristic time
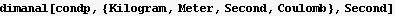
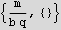
Find characteristic energy
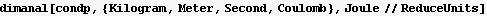
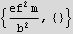
b) Find the analytic solution to the equations of motion. What is the period of the motion? What is the maximum and minimum values of the kinetic energy of the particle as a function of time? Comment on how these quantities are related to the characteristic values found in part a.

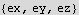
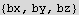
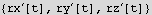
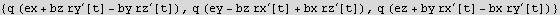
Now since we are told that E is constant and along the x direction only, we set the electric field vector coordinates that way. Also since we are told that the magnetic field B is constant and along the z direction, we set its coordinates to point that way as well.
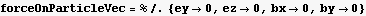
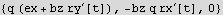
Declare a position vector
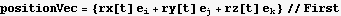
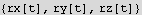
Declare the ODE using F=ma
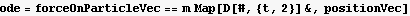
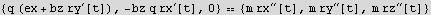
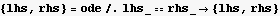
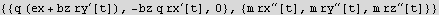
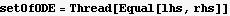
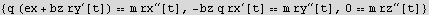

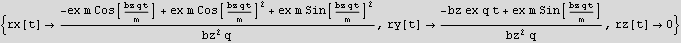
Find the period.
From above we see that the x component of the position contains a frequency ω = bz q/m. Hence the period is 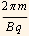
Verify the units
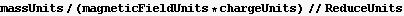
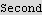
For the motion along the y axis, the period is also given by the same value above
Find K.E.
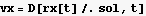
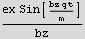
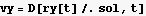
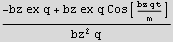
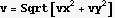
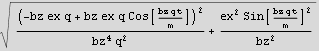
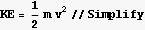
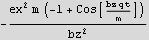
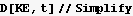
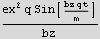
The above is zero when 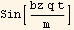 =0, which means
=0, which means 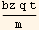 =nπ for n=0,1,2,3,...
=nπ for n=0,1,2,3,...
n=0 means t=0, then K.E. is minimum because then KE=0 (initial condition, particle is still at rest)
look at the next value. When n=1 then 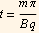 then KE is
then KE is
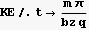
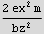
When n=2 then 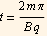 find what is KE now
find what is KE now
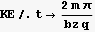
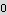
Hence we see that for n=1,3,5,7,....KE is max, and when n=0,2,4,6,... KE is min.
hence MAX KE is 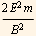 which occurs at times t= n
which occurs at times t= n  for ODD n
for ODD n
and MIN KE is 0 which occurs at times t=n  for EVEN n
for EVEN n
Now I Comment on how these quantities are related to the characteristic values found in part a.
From part (a) we found that the energy is proportional to 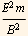 and here we just found the maximum KE is
and here we just found the maximum KE is 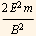 , Hence this agree with the finding for the KE energy part with a proportionality constant of 2.
, Hence this agree with the finding for the KE energy part with a proportionality constant of 2.
In part(a) we found the time scale to be proportional to 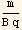 and here we found the period to be
and here we found the period to be 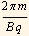 which agree with part (a), and the proportionality constant is 2 π
which agree with part (a), and the proportionality constant is 2 π
In part(a) we found the length scale to be  , and here we found the period to be
, and here we found the period to be 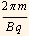 , and since the velocity is as shown above, I can find the distance travelled during one period, and this is taken as the length scale. Let me find this distance now:
, and since the velocity is as shown above, I can find the distance travelled during one period, and this is taken as the length scale. Let me find this distance now:

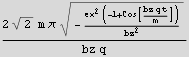
The stuff under the square root above can be written as K 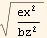 for some constant K, hence the distance above can be written as
for some constant K, hence the distance above can be written as
 which is
which is
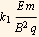
Where 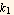 is a new constant which consumed (k
is a new constant which consumed (k 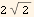 π)
π)
Comparing the above expression for the distance, we see it agrees which part (a), where the proportionality constant is 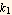
c) For the special case of a proton in an E field of 1000 Volts/meter and a B field of 0.1 Tesla, draw a graph of the trajectory of the particle.
First check what the period is now that we have some numbers to work with
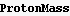
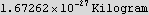
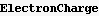
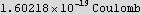
Hence period is (in seconds):
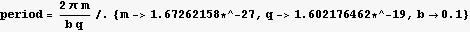
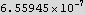
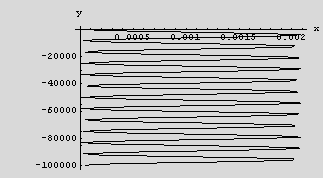
Now generate plot points to make a plot of the trajectory of the particle
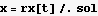
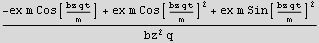
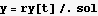
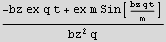

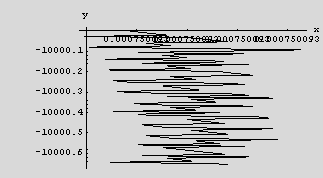
This plot is tricky, I make another plot with longer time intervals, it shows the periods better
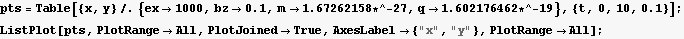
14. (grads) Let y[x] be a curve with endpoints symmetrically positioned about the y axis. Consider the surface area of the surface generated by rotating y[x] about the x axis to make a surface of revolution. Find the y[x] which yields the surface of minimum area. This is the shape adopted by a soap film supported by two circular hoops; the soap film minimizes its surface area because there is an energetic cost per unit of area of film.

a) Write an expression for the surface area in terms of an integral.
Imagine a thin strip all the way around. This strip will have differential width of
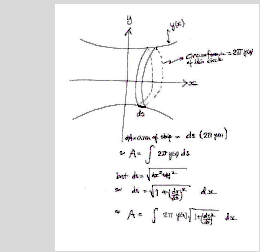
ds = 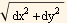
Hence the strip will have an differential area of
dA= circumference * ds = 2π*y[x] * 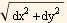
Now assume x goes from -1 to +1. (or we can write -L to +L, it does not matter). Now, due to symmetry, we integrate from x=0 to 1 and multiply by 2.
Hence the area A= 2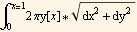
But 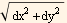 =
=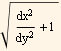 dy
dy
OR
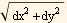 =
=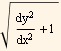 dx
dx
I will pick the First form above.
Hence substitute the above into the area integral A we get
A= 4π dy
dy
b) Find the Euler equation for the extremal curves.
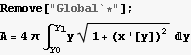
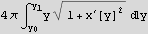
Minimizing A leads to the Euler equation (which comes from writing the function we want to minimize as F(y,x,x'[y]), and it leads to the euler equation which is
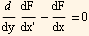
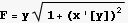
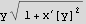
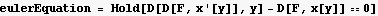
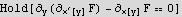
Look at the last term above
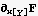
Hence eulerEquation becomes now just the first term, which is
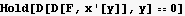
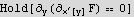
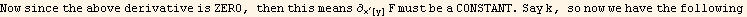
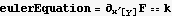
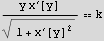
c)Solve the resulting DE and look for solutions which are symmetric about the y axis. Show that the solutions are of the form A Cosh[b x] .
Square both sides above, we get
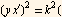
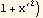
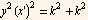
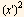
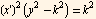
Hence
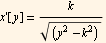
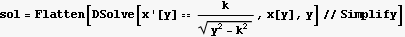

I need to convert the above to Cosh. I do not know how to make Mathematica do it, so searching the Tables reference Handbooks I found the following trig. Relationship
ArcCosh(Z) = Log( Z + 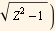
Hence in the solution I have above, I can rewrite it as follows to convert things to Cosh as needed by this problem
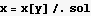
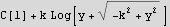
Rewrite as follows
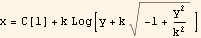
or
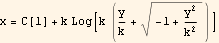
But Log[A*B] = some constant * Log[B] so above becomes
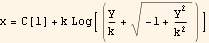
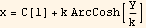
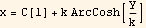
Hence, let C[1]=K1, we write the above as
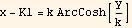
Hence
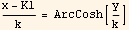
or
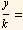 Cosh
Cosh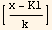
hence
y[x] = K 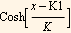
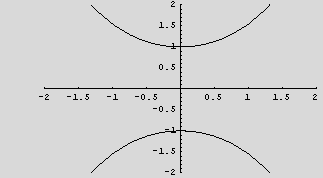
Now Plot it, assume some constants
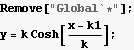
by trial and error, for {k→1,k1→0} I get the symmeterial picture I needed. For different constants, the plots are shifted to left or right.
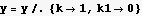
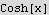
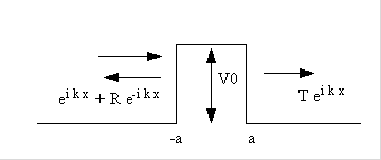
15.(grads) Quantum tunneling is one of the characteristic non-intuitive phenomena of quantum mechanics. Consider a beam of particles of unit density traveling to the right, represented by 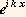 , as shown in the figure below. The beam encounters a region of space where the potential energy is V0. For a classical particle, if the incident kinetic energy Ein=
, as shown in the figure below. The beam encounters a region of space where the potential energy is V0. For a classical particle, if the incident kinetic energy Ein=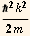 <V0 the particle would reflect off the barrier, while if
<V0 the particle would reflect off the barrier, while if 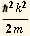 >V0 , the particle would pass through. For a quantum particle, some fraction of the beam is reflected, as represented by the R
>V0 , the particle would pass through. For a quantum particle, some fraction of the beam is reflected, as represented by the R 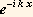 term, and some fraction is transmitted, as represented by the T
term, and some fraction is transmitted, as represented by the T 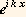 term.
term.
I wish I have time to attempt this problem as it looks interesting but I have not yet started on HW9 which is due in 2 days, I better start on that now.
The Schrodinger equation that governs this problem inside the barrier is
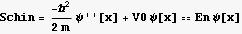
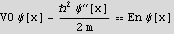
and outside:
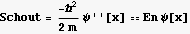
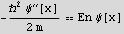
T is the transmission amplitude. The object of primary interest in this problem is the behavior of the transmission probability given by 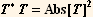 as a function of the initial energy Ein=
as a function of the initial energy Ein=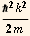 . Graphs of the transmission probability as a function of energy are shown in most quantum books, but the algebra required to construct the plot is not trivial.
. Graphs of the transmission probability as a function of energy are shown in most quantum books, but the algebra required to construct the plot is not trivial.
a) Using k as the primary variable as suggested in the Figure above, write down solutions in each of the three regions. The central region will involve 2 unknown parameters. Invoke the requirement that the solutions must be continuous and have continuous first derivative at the boundaries of the regions. Use this to solve for all of the unknown parameters.
b) What are the natural units of length and energy for this problem? Also identify any dimensionless parameters.
c) Express T as found in part a) in terms of Ein rather than k.
d) Using the characteristic energy found in b) , express T in terms of a reduced dimensionless energy Er
e) T(Er) still contains a and V0. Eliminate these using the dimensionless parameter found in b) . When this is done, you should have the transmission amplitude as a function of strictly dimensionless quantities. Note that this implies that the transmission amplitude is not a function of a and V0 separately, but only a special dimensionless combination of them.
d) Make a plot of Abs[T]^2 as a function of the reduced energy for values of the dimensionless parameter=4, 1, 1/4 .
e) extra credit. Find a compact expression for 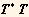 . Simply computing this using ComplexExpand and Conjugate yields a rather complicated expression containing Arg or ArcTan which are necessary to specify the signs of various parameters. Judicious rules to deal with these terms will yield a pleasant expression. Compare plots of this expression with those you made d).
. Simply computing this using ComplexExpand and Conjugate yields a rather complicated expression containing Arg or ArcTan which are necessary to specify the signs of various parameters. Judicious rules to deal with these terms will yield a pleasant expression. Compare plots of this expression with those you made d).