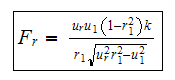HW2. CEE 247. Structural Dynamics. UCI. Fall 2006
Nasser Abbasi
Solution
The rotating mass generates a force of
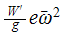 where
where
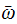 is the angular speed of the rotating weight and
is the angular speed of the rotating weight and
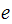 is the distance of the mass from the center of the motor.
is the distance of the mass from the center of the motor.
Hence the vertical load is
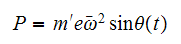 But
But
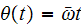 ,
hence the vertical force is
,
hence the vertical force is
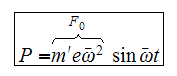
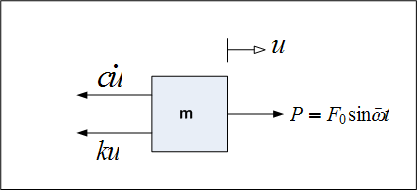
The physical idealized model is
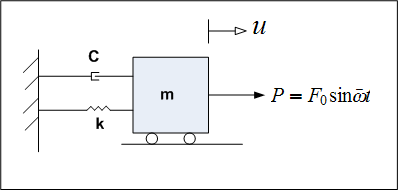
Hence the equation of motion can now be written from the free body diagram as
(where
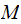 is the mass of the electric motor) and assuming the mass is moving to the
right, and taking
is the mass of the electric motor) and assuming the mass is moving to the
right, and taking
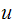 relative to the static equilibrium position.
relative to the static equilibrium position.
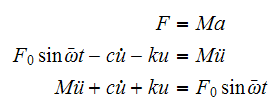
The above ODE has the solution
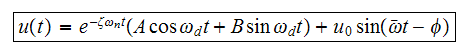
Where
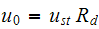 ,
where
,
where
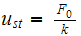 and
and
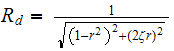 and
and
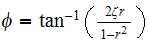 and
and
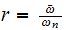 and
and

At steady state, the transient solution decays to zero thanks to the negative exponential term in it, and the solution becomes
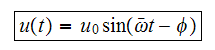
Which has amplitude of
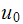 .
Hence we need to evaluate
.
Hence we need to evaluate
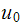
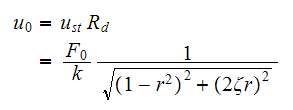
But motor runs at
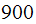 rpm, hence
rpm, hence
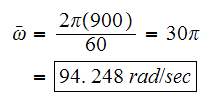 We are given that
We are given that
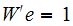 lb.in, Hence
lb.in, Hence
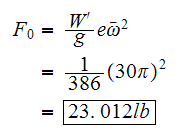
Now we need to find
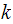 ,
the stiffness of the beam against bending. For this geometry,
,
the stiffness of the beam against bending. For this geometry,
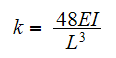
But
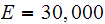 ksi for steel, and for
ksi for steel, and for
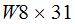 from tables we find
from tables we find
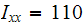 in
in ,
hence
,
hence
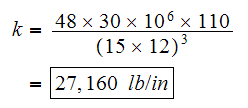
Now to find
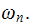 Recall
that that
Recall
that that
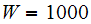 lb, hence
lb, hence
 Hence
Hence
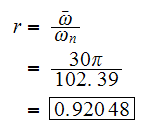
Putting all these together we obtain
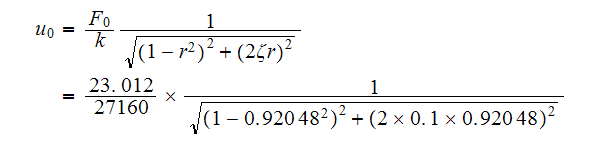
Hence
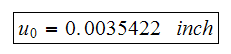
(Note: The back of the book gives
 ,
I think the book used a slightly different steel table to obtain
,
I think the book used a slightly different steel table to obtain
 which could have been slightly different than the one I used.)
which could have been slightly different than the one I used.)
solution
From the free body diagram:
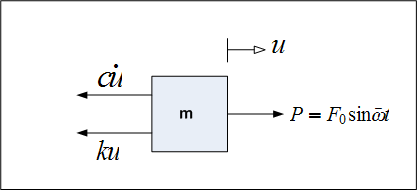
We see that the forces transmitted to the support are
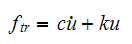
Where
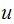 here is taken as the steady state solution from problem 3.2, which is
here is taken as the steady state solution from problem 3.2, which is
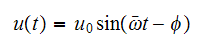
Where
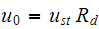 ,
and
,
and
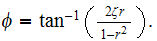 Differentiate the above equation and substitute the results back into the
Differentiate the above equation and substitute the results back into the
 equation we obtain
equation we obtain
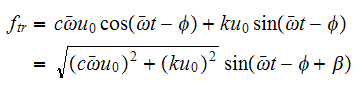
Where
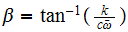
Hence we see that the maximum force transmitted to the supports are given by
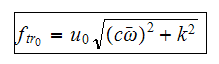
We now plug into the above equation the results we obtain from problem 3.2 to
determine
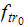 .
All the variables in the above expression are known, which are repeated here
.
All the variables in the above expression are known, which are repeated here
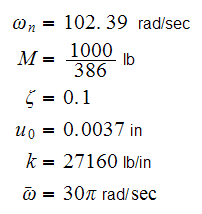
We just need to find the damping
 .
Since
.
Since
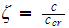 and
and
 ,
hence
,
hence

Hence
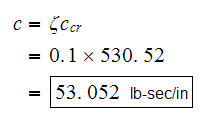
Now substitute all the above values into equation (1) we obtain
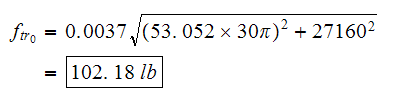
solution
The physical idealized system is the following
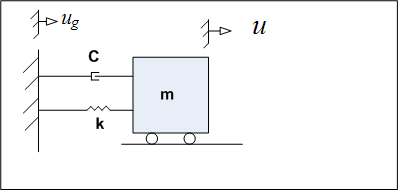
Where in the above,
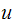 is
the absolute displacement of the tower, and
is
the absolute displacement of the tower, and
 is the absolute displacement of the ground. The free body diagram is
is the absolute displacement of the ground. The free body diagram is
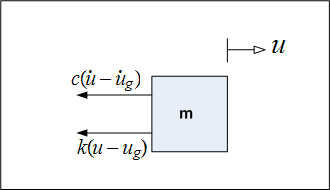
Applying newton's second law we obtain
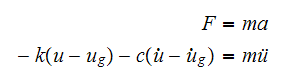
Expand and rearrange
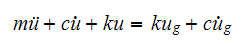
Let the relative motion between the mass and the ground be
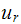 ,
hence
,
hence
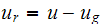 or
or
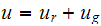 ,
similarly
,
similarly
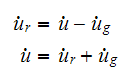
And
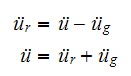
Using the above expressions for
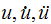 ,
we can now rewrite (1) as
,
we can now rewrite (1) as
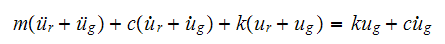
Expand (2) and cancel terms we obtain
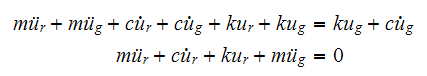
Or
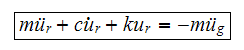
The above is the equation of motion of the tower using relative displacement.
Hence we can view the term
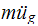 as the effective force acting on the tower due to the acceleration of the
ground.
as the effective force acting on the tower due to the acceleration of the
ground.
Now using the fact that the ground motion is harmonic, we can write
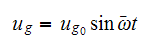
Where
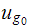 is the maximum amplitude of the ground displacement, and
is the maximum amplitude of the ground displacement, and
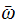 is the ground motion frequency. Hence from the above we obtain that
is the ground motion frequency. Hence from the above we obtain that

Plug the above into (3) we obtain
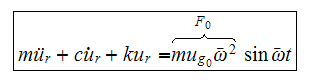
The above is now in standard 2nd order linear system, the steady state
solution for
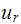 is
is
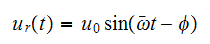
Where
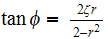 and
and
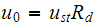 ,
where
,
where
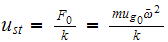 ,
and
,
and
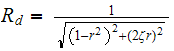
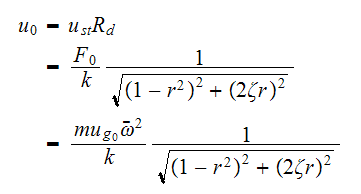
But we are told that
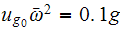 ,
Hence the above becomes
,
Hence the above becomes

We are given that
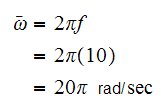
and
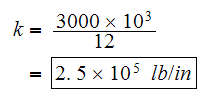
Then
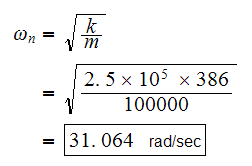
Then
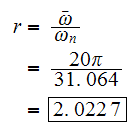
and since
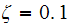 we obtain
we obtain
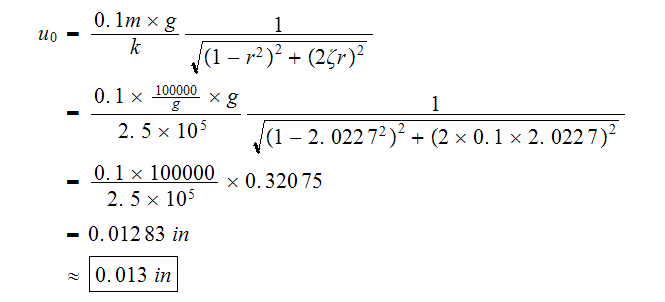
Determine the transmissibility of the above problem
Solution
We need to determine first the expression that represents the force that is transmitted to the ground. From the idealized system diagram
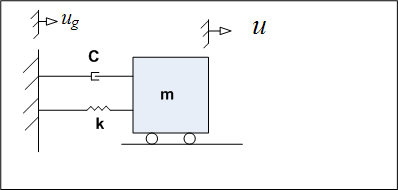
We see that the force transmitted to the support is
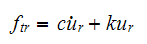
But
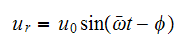
Where
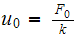 where
where
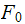 here is the effective force.
here is the effective force.
Hence
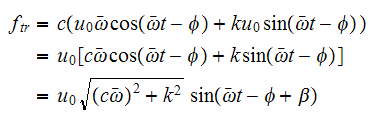
Where
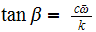
Hence Max force transmitted is
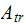
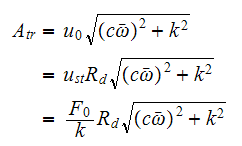
But
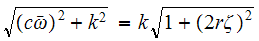 hence
hence
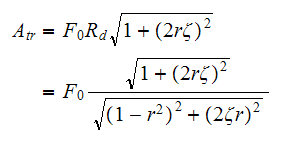
But
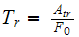 hence
hence
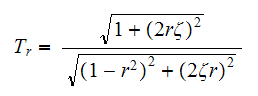
Now, since from the earlier problem we found that
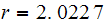 ,
and given that
,
and given that
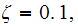 then
then
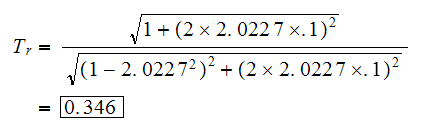

Solution
We start with the expression for the maximum amplitude steady state displacement given by
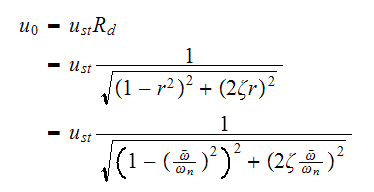
We have 2 cases, case 1 is when
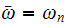 (resonance), and the second case is when
(resonance), and the second case is when
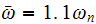 .
Hence we obtain the following equation
.
Hence we obtain the following equation
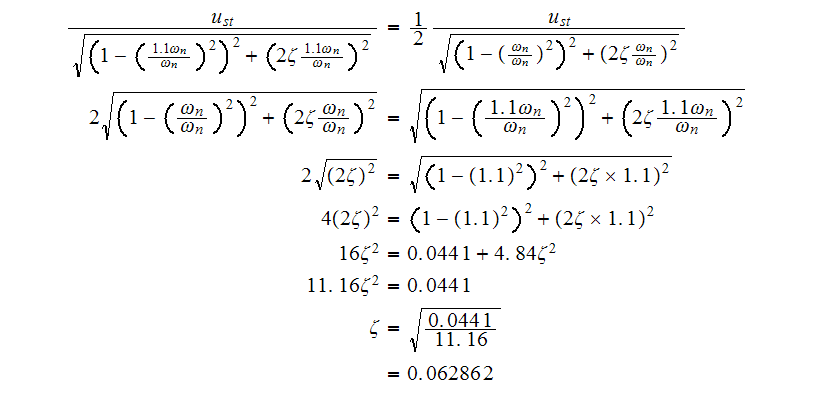
Hence
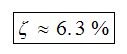
Solution
Considering maximum amplitude of steady state is given by
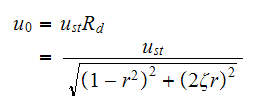
But

We are given one case where
 (resonance) and another case where
(resonance) and another case where
 .When
.When
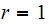 ,
we obtain
,
we obtain
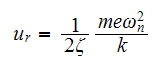
When
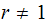 we write (where we call
we write (where we call
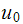 when
when
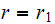 as
as

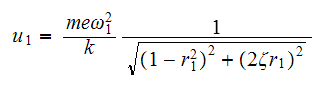
Square equation (1) and (2) and divide by each others we obtain
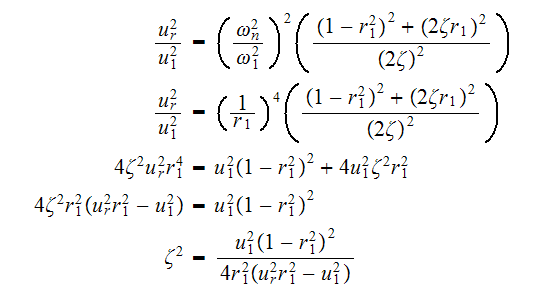
Hence
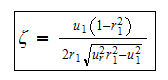
Since
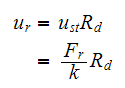
Hence
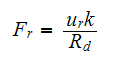
But
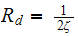 at resonance, hence
at resonance, hence
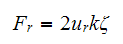
But from first part, we found expression for
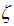 ,
which we plug into the above to obtain
,
which we plug into the above to obtain
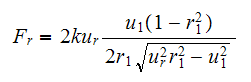
Hence