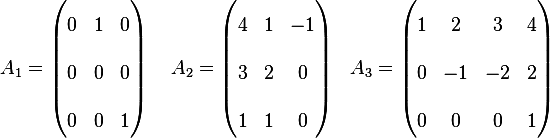
Find the rank and nullities of the following matrices
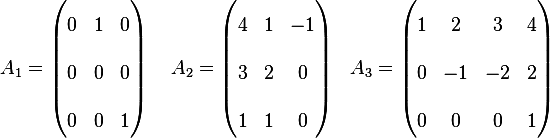
Solution
Solution method: First find the rank of the matrix, then to find the nullity, use the relation
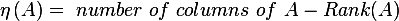
The rank of a matrix can be found using one of the following methods
 of the matrix. The number of unique
of the matrix. The number of unique 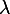 is the rank of the
matrix. This works only on square matrices.
is the rank of the
matrix. This works only on square matrices. Hence for 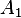 using the second method above, we see that the minor found by omitting the
first columns and the second row is
using the second method above, we see that the minor found by omitting the
first columns and the second row is 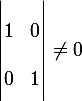 but the full determinant is clearly zero (since
but the full determinant is clearly zero (since 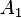 has one columns which is all zeros, since any square matrix which has all zero's in one of its rows or
columns must have zero determinant). Hence the largest size of a minor which is not zero is 2,
hence the rank is 2
has one columns which is all zeros, since any square matrix which has all zero's in one of its rows or
columns must have zero determinant). Hence the largest size of a minor which is not zero is 2,
hence the rank is 2
Since the rank is 2, then 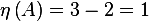
For 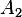 ,
, 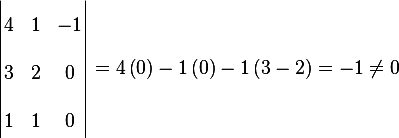 hence the rank is 3
hence the rank is 3
Therefor 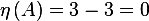
For 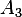 , the rank can not be more than 3, and since the last row contains zeros
in the first 3 elements, I will select the minor to test on as the last 3 columns, hence
, the rank can not be more than 3, and since the last row contains zeros
in the first 3 elements, I will select the minor to test on as the last 3 columns, hence
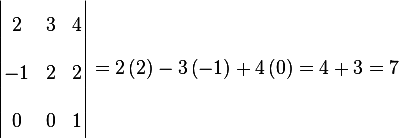
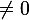 , hence the rank is 3
, hence the rank is 3
question: Find bases of the range spaces and the null spaces of the matrices in problem 3.5
solution method: To find the bases for the range space, all what we need to do is to find 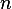 linearly independent vectors where
linearly independent vectors where 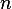 is the rank of A found above. To find bases for the null space
of A, since we know the rank of the null space, and the dimension of the rank space, we
need to find m linearly independent vectors where
is the rank of A found above. To find bases for the null space
of A, since we know the rank of the null space, and the dimension of the rank space, we
need to find m linearly independent vectors where 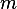 is the rank of the null space of
A.
is the rank of the null space of
A.
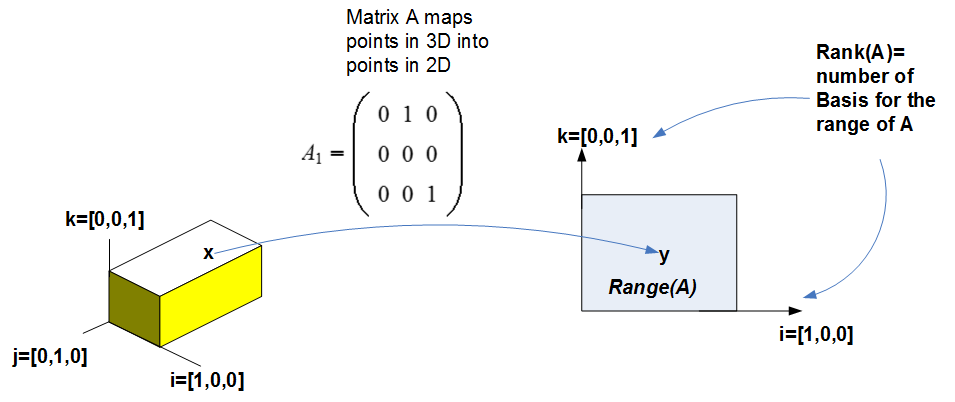
A1: Since 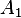 has rank of 2, this means that range(A) has dimension 2. In other words
A maps a 'point' in a 3D volume to a 'point' of in a 2D flat plane. Hence we can use either
has rank of 2, this means that range(A) has dimension 2. In other words
A maps a 'point' in a 3D volume to a 'point' of in a 2D flat plane. Hence we can use either 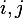 or
or
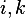 or
or 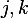 as the basis of the range of A. But since
as the basis of the range of A. But since 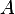 has zeros in its second row, this means
that there are no points in the range of A which has a component along the
has zeros in its second row, this means
that there are no points in the range of A which has a component along the 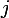 dimension. Hence
the only plane left is the one spanned by
dimension. Hence
the only plane left is the one spanned by 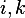 or
or 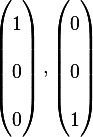 . This is illustrated by the following
diagram
. This is illustrated by the following
diagram
since the rank of the null space is 1, then we need to find one vector 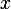 s.t.
s.t. 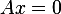
Hence 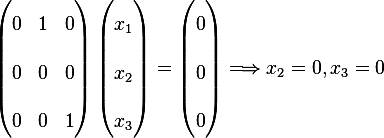 , hence a basic is
, hence a basic is  where 'any'
could be any number. select 1 to make it normalized, hence a basis is for the null space is
where 'any'
could be any number. select 1 to make it normalized, hence a basis is for the null space is

A2: Since 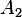 has rank of 3, and this is equal to the number of columns in A, then A maps a
point in 3D vector space
has rank of 3, and this is equal to the number of columns in A, then A maps a
point in 3D vector space  to a point in 3D vector space
to a point in 3D vector space 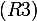 . Then we can use
. Then we can use 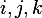 as its
bases. i.e.
as its
bases. i.e. 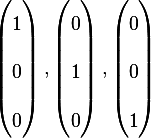
Since the rank of the null space of A is zero, then the null space of A is  , hence no basis
for the null space as it is empty.
, hence no basis
for the null space as it is empty.
A3: Since 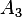 has rank of 3, then we need to find 3 linearly independent vectors to span the
range of A. Select
has rank of 3, then we need to find 3 linearly independent vectors to span the
range of A. Select 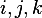 as its bases. i.e.
as its bases. i.e. 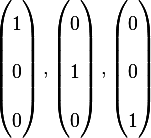
The null space of  is 1, then we need to find one vector such
is 1, then we need to find one vector such  and normalize it as
needed.
and normalize it as
needed.
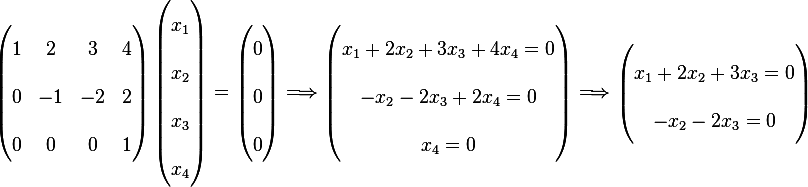
Hence 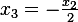 and so
and so 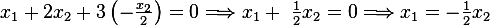
Hence if we take 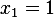 , then
, then 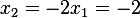 and then
and then 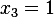
Consider the linear algebraic equation 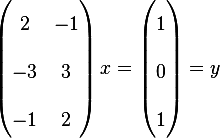 , it has 3 equations and 3
unknowns. Does a solution exist in the equation? Is this solution unique, Does a solution exist if
, it has 3 equations and 3
unknowns. Does a solution exist in the equation? Is this solution unique, Does a solution exist if
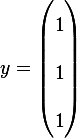
Solution
A solution exist if A spans a space which contains 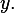 Since
Since 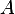 has 2 columns we see that it
takes points from 2D space and send these points to its range space. Since the rank of A is 2 (since
has 2 columns we see that it
takes points from 2D space and send these points to its range space. Since the rank of A is 2 (since
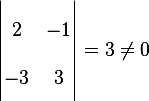 ) then the dimension of its range space is 2, i.e. it maps points from 2D space to
2D space. Solve this is by solving for
) then the dimension of its range space is 2, i.e. it maps points from 2D space to
2D space. Solve this is by solving for 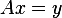 and to see if we can find a vector
and to see if we can find a vector 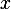 to satisfy this
equation as follows
to satisfy this
equation as follows
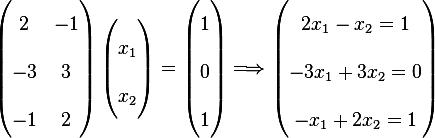
From second equation we see that 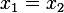 , substitute this in either equation 1, we get
that
, substitute this in either equation 1, we get
that 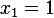 , hence
, hence 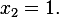 Sub this solution in equation 3 we see that is also satisfy
it.
Sub this solution in equation 3 we see that is also satisfy
it.
Hence we found a point 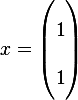 , which is mapped by A to point
, which is mapped by A to point  hence a solution
exist.
hence a solution
exist.
Since the null space is empty, then this solution is unique.
When 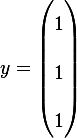 , we need to try to see if there is an
, we need to try to see if there is an  such that
such that 
From first equation,  sub into second equation we get
sub into second equation we get
Hence 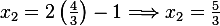
Now sub this solution into the third equation we get 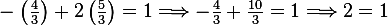 which is not valid. Hence no solution exist.
which is not valid. Hence no solution exist.
Problem: Consider 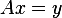 , where
, where 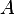 is an
is an 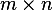 and has rank
and has rank 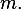 is
is 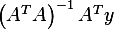 a
solution? if not, under what condition will it be a solution? is
a
solution? if not, under what condition will it be a solution? is 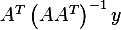 a solution?
a solution?
Solution
First we need to determine if 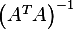 exist.
exist.
Since 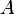 is an
is an 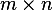 then
then 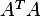 is
is 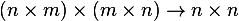 matrix.
matrix.
Hence 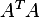 is a square matrix of dimension
is a square matrix of dimension 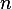 . Since we are told the rank is
. Since we are told the rank is 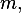 and the
rank of a matrix is the smaller of its dimensions (the smaller of its rows or columns if they are not
the same), hence there exist only
and the
rank of a matrix is the smaller of its dimensions (the smaller of its rows or columns if they are not
the same), hence there exist only 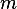 linearly independent rows, and not
linearly independent rows, and not 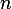 linearly independent
rows. hence
linearly independent
rows. hence 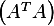 is NOT invertible
is NOT invertible 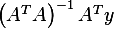 is not a solution.
is not a solution.
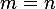
. Since in this case 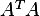 can be inverted.
can be inverted.
Second part:  is
is 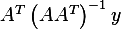 a solution?
a solution?
Since 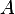 is an
is an 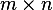 then
then 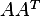 is
is  matrix.
matrix.
Hence, since we are told the rank is 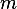 then there exist
then there exist 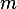 linearly
independent rows, hence
linearly
independent rows, hence 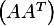 is invertible. Hence
is invertible. Hence 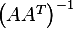 exist, and so
exist, and so
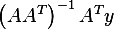 can be computed. And in addition, if we multiply this by
can be computed. And in addition, if we multiply this by 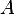 we get
we get
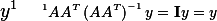 hence it is a solution.
hence it is a solution.