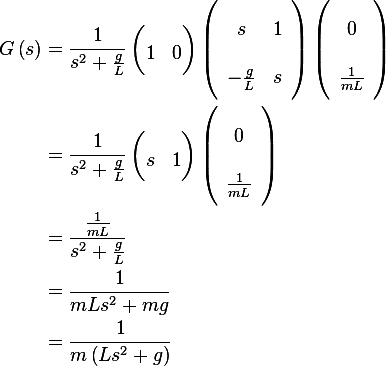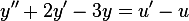
Consider the system described by
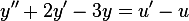
What are the transfer function and the impulse response of the system?
Answer
The transfer function is defined as the ratio of the Laplace transform of the output to the
laplace transform of the input assuming zero initial conditions. i.e. assume that 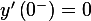 ,
,
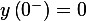 ,
, 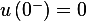
Taking the laplace transform of the above differential equation we obtain
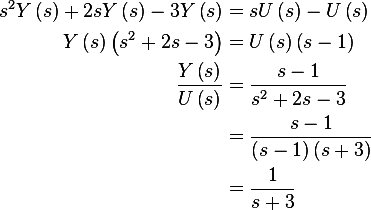
Hence
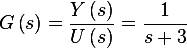
Hence the impulse response is the inverse laplace transform of 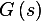 , which is for this simple
case can written directly
, which is for this simple
case can written directly
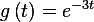
Note: the above solution is valid for 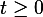 . For
. For 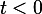 the impulse response is zero.
the impulse response is zero.
Find state space equations to describe the pendulum system in following figure. Write down the
linearized dynamic equations and the transfer function from 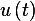 to
to 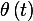
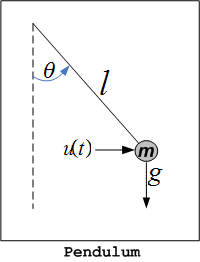
Answer
The general state space representation for this system is
To simplify notations, I will not list time as an independent variables since it is implicit in 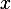 and
and 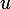 in this problem.
in this problem.
Now, assume we have a nominal solution 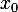 and a nominal input
and a nominal input 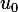 and let the perturbation
from these be
and let the perturbation
from these be 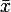 and
and 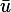 respectively. Hence (1) can be written as
respectively. Hence (1) can be written as
Now pick a nominal solution when the system is in its stable equilibrium position (when the pendulum is hanging down at rest).
Hence 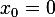 and
and 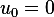 . For this state and input we obtain
. For this state and input we obtain 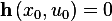 since
since 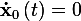 as there is no state change with time, also we obtain that
as there is no state change with time, also we obtain that 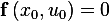 since
since 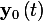 since the
mass is not moving. Hence (2) becomes
since the
mass is not moving. Hence (2) becomes
Now since 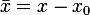 and
and 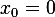 then
then 
Similarly, 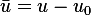 and
and 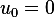 then
then 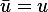 hence (3) can be written as
hence (3) can be written as
Hence we just need to evaluate 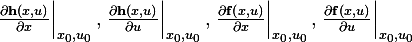 to obtain the
linearized solution.
to obtain the
linearized solution.
Since there are 2 states in this system and one input we obtain
Now we need to find 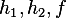 and substitute these into (5) and then into (4) to find the
solution.
and substitute these into (5) and then into (4) to find the
solution.
First find the dynamic equation for this system. The forces on the mass are
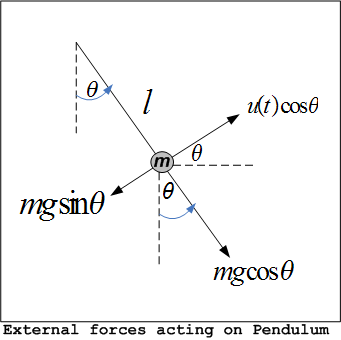
Applying Newton second law 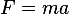 , along the direction tangent to the motion we
get
, along the direction tangent to the motion we
get
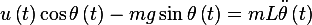
Hence
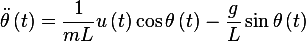
Now convert to state space. Let 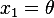 and
and 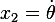 .
.
Hence
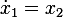
and
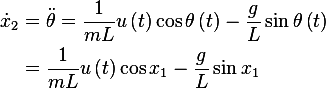
Hence we can write
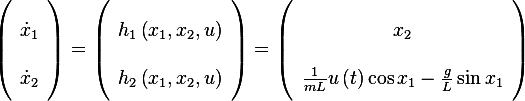 | (6) |
Now for the output equation:
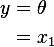
Hence
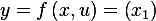
Now that we know 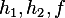 , we can go back to (5) and evaluate that, we obtain
, we can go back to (5) and evaluate that, we obtain
Now to obtain the solution (4) we need to evaluate (7) at the nominal solution 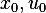 and these
are zero, i.e.
and these
are zero, i.e. 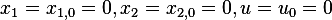 then (7) becomes
then (7) becomes
Hence, substitute (8) into (4) we obtain the final linearized solution
The above is the linearized solution. Where
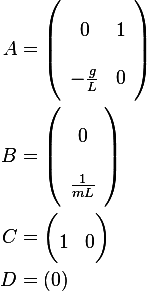
The transfer function is
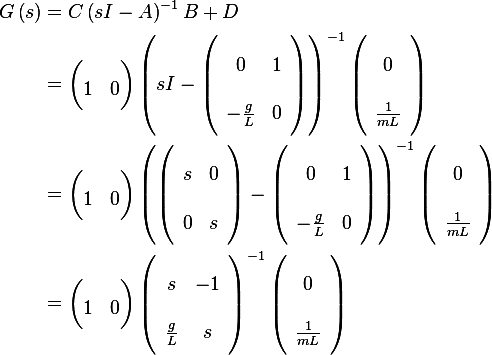
but
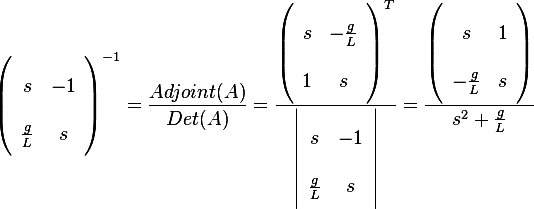
Hence