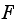 .
.
HW 4, EECS 203A
Problem 4.9
Nasser Abbasi, UCI. Fall 2004
Question
Solution
The operation that causes the image to flip is taking the complex conjugate of
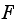 .
.
Explanation of each step:
Multiplying the original image by
 has the effect related to centering the spectrum in the center of the spectrum
image.
has the effect related to centering the spectrum in the center of the spectrum
image.
DFT generates the spectrum, with
 in the center due to step (1).
in the center due to step (1).
Computing IDFT gets back the image.
Multiplying image from step (3) by
 again is to reverse the effect on the image done by step (1).
again is to reverse the effect on the image done by step (1).
So, only step that can cause the image to flip as shown is taking the complex conjugate, which is a step done between steps (2) and (3) above.
To explain it mathematically. The IDFT is
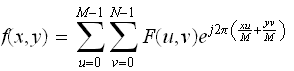
In the above
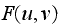 is complex in general, and is being multiplied by a complex number
is complex in general, and is being multiplied by a complex number
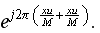
when we multiply two complex numbers together, We multiply the magnitudes, and add the phases.
Hence, when we obtained the complex conjugate of
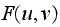 ,
(we negated the complex part of the number), we effectively flipped its phase
upside down, i.e. complex numbers
,
(we negated the complex part of the number), we effectively flipped its phase
upside down, i.e. complex numbers
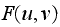 that used to be in the first quadrant, now reside in the 4th quadrant, and
those in the second quadrant, now in the 3rd quadrant, those in the 3rd
quadrant now move to the 2nd quadrant, and those in the 4th quadrant now move
to the first quadrant. i.e. complex numbers
that used to be in the first quadrant, now reside in the 4th quadrant, and
those in the second quadrant, now in the 3rd quadrant, those in the 3rd
quadrant now move to the 2nd quadrant, and those in the 4th quadrant now move
to the first quadrant. i.e. complex numbers
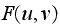 that used to be in the top half will now be in the bottom half of the complex
plane, and vise versa.
that used to be in the top half will now be in the bottom half of the complex
plane, and vise versa.
Now when we multiplied those new values
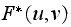 with
with
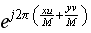 ,
each resulting complex number will be have new positions that are switched
upside down w.r.t. its phase as compared to not having taken the complex
conjugate.
,
each resulting complex number will be have new positions that are switched
upside down w.r.t. its phase as compared to not having taken the complex
conjugate.
The above only explains a mirror image flip across a horizontal line in the middle of the image of one complex number. This still does not explain the mirror image flipping across a vertical line in the middle of image shown.
This can be now explained due to the sum being done on each of these complex numbers.
Each multiplication
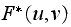
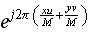 generates one complex number whose phase is flipped with respect to the
horizontal line as explained above. Consider this as a new vector in the
complex plane. As we sum more such vectors, as we evaluate the
generates one complex number whose phase is flipped with respect to the
horizontal line as explained above. Consider this as a new vector in the
complex plane. As we sum more such vectors, as we evaluate the
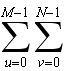 across all the
across all the
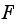 complex plane, and using vector additions, we see that the resulting sum
vector will drift slowly to the left plane (if it used to be in the right side
plane had we not taken the complex conjugate) or will drift to the right half
of the plane (if it used to be in the left half of the plane had we not taken
the complex conjugate).
complex plane, and using vector additions, we see that the resulting sum
vector will drift slowly to the left plane (if it used to be in the right side
plane had we not taken the complex conjugate) or will drift to the right half
of the plane (if it used to be in the left half of the plane had we not taken
the complex conjugate).
Then the result is that we have a flip of the image across the horizontal middle line of the image, and a flip across the vertical middle line of the image, resulting in the image shown.