HOME
HW 15 Mathematics 503, Mathematical Modeling, CSUF
, August 6, 2007
Nasser M. Abbasi
June 15, 2014
Contents
1 Problem 6 page 346 section 6.2 (PDE's)
problem:
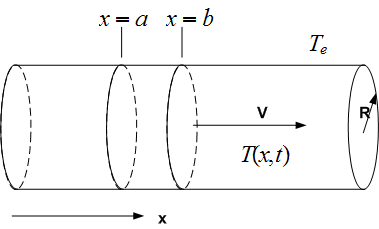
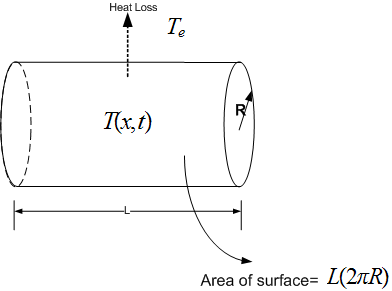
A fluid having density 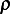 , specific heat
, specific heat  , and heat conductivity
, and heat conductivity 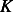 , flows at a constant velocity
, flows at a constant velocity 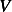 in a
cylindrical tube of length
in a
cylindrical tube of length 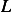 , and radius
, and radius 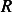 . The temperature at position
. The temperature at position 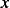 is
is 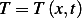 and diffusion of
heat is ignored. As it flows, heat is lost though the lateral side at a rate jointly proportional to
the area and to the difference between the temperature
and diffusion of
heat is ignored. As it flows, heat is lost though the lateral side at a rate jointly proportional to
the area and to the difference between the temperature 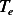 of the external environment and the
temperature
of the external environment and the
temperature 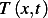 of the fluid (Newton's law of cooling). Derive a PDE model for the temperature
of the fluid (Newton's law of cooling). Derive a PDE model for the temperature
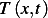
Find the general solution of the equation by transforming to a moving coordinates system
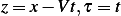
Answer:
|
|
|
| Term | Definition | Units (SI) |
|
|
|
| heat
conductivity
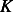 | The quantity of heat that passes in unit time through unit area
of a substance whose thickness is unity, when its opposite
faces differ in temperature by one degree | 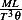
|
|
|
|
| Specific heat
 | the amount of heat needed to raise a unit mass by one degree. | 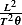
|
|
|
|
| Density 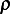 | density | 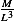
|
|
|
|
| |
First we need to decide on the quantity over which we are applying the balance equation over. We solve
this problem 2 times. The first by using the amount of heat as the quantity. Next we solve the problem by using
the density of heat as the quantity.
Using amount of heat as the quantity to apply
balance equation on
Apply the energy balance equation. Consider 2 cross sectional area at 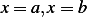 .
.
Total amount of heat inside this volume = mass of fluid inside this volume 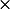 specific heat
specific heat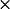 its
temperature
its
temperature 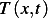
Hence amount of heat between 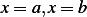 is
is
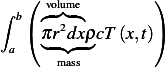
Now consider the rate that heat flows in/out the volume between  and
and 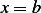 , this is given
by
, this is given
by
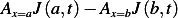
and since the area does not change, this is the same as
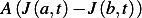
where 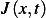 is the amount of heat that flows though a unit area per unit time. (the Flux)
is the amount of heat that flows though a unit area per unit time. (the Flux)
Now there is some heat loss due to cooling via the lateral side. Use Newton law of cooling which says that
the amount of heat a body loses per second is proportional to temperature difference between
it and its surrounding temperature, and proportional to the area of the body though which heat
is lost. The constant of proportionality is 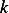 . The area of the body in this case is the surface of
the cylinder of strip of width
. The area of the body in this case is the surface of
the cylinder of strip of width 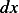 which is given by
which is given by 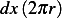 when considering a differential
length.
when considering a differential
length.
Hence lateral heat loss rate between  and
and 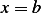 is
is ![[ ∫ b ]
− a k dx(2πr )(T (x,t)− Te)](ma36x.png) . The minus sign is
to say that this is considered to be a heat loss, not gain, into the volume under consideration. Now need to find
what the units of this
. The minus sign is
to say that this is considered to be a heat loss, not gain, into the volume under consideration. Now need to find
what the units of this 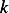 is (this is NOT the heat conductivity coefficient). Using dimensional analysis, we
write
is (this is NOT the heat conductivity coefficient). Using dimensional analysis, we
write
![[rate of heat]](ma38x.png) =
= ![[ML2]
[k][L2][𝜃]→ [k]= [rate-of-heat]= --[heat]- = ---T2- =
[L2][𝜃] [L2][𝜃][T] [L2][𝜃][T]](ma39x.png)
![-[M]--
[𝜃][T3]](ma40x.png)
So to obtain the energy balance we write
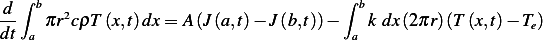
Move the differentiation inside and assuming constant density throughout
Now apply fundamental law of calculus to the flux term in the RHS we have
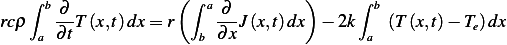
Changing the limits of integration on the RHS to make it match the LHS and canceling 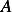 we
obtain
we
obtain
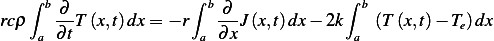
Because the above holds for all intervals of integration and the functions involved are continuous, then we
can remove the integrals and just write
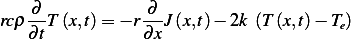
For flux, consider the advection model, hence 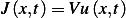 where
where 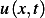 is amount of heat per unit
volume at
is amount of heat per unit
volume at 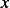 , but this is the same as
, but this is the same as 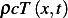 , hence
, hence 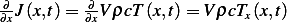 since
since 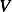 is
constant, then the above becomes
is
constant, then the above becomes
Hence the PDE is
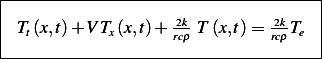
Let me check dimensionality. Each term above should have the same units.
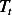 has units
has units ![[𝜃]
T](ma56x.png)
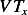 has units
has units ![[-L𝜃] [𝜃 ]
T L = T](ma58x.png)
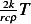 has units
has units ![[ M ]
-T32𝜃𝜃- = [-𝜃]
LTL2𝜃 ML3 T](ma60x.png)
Hence the PDE is dimensionality correct. Now I have more confidence it is correct. Now we solve the
same problem by using the density of heat.
Using density of amount of heat as the quantity to
apply balance equation on
density of heat is 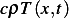 , hence rate of change of density of heat is
, hence rate of change of density of heat is 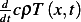
For the flux term, using the advection model, we obtain that
Hence
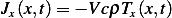
Now for heat loss,
Hence the balance equation now becomes
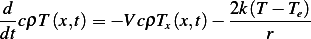
Hence
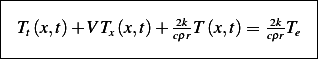
Which matches the results obtained earlier.
Now complete the problem. Find a general
solution.
Let 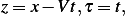 Hence
Hence
and
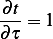
Let 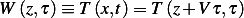 , therefore
, therefore
But from the PDE itself which we derived above, we see that 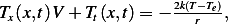 Hence
Hence
![|--------------------------------|
| W (z,τ)= − 2k[T (z+ V τ,τ )− T] |
| τ r e |
---------------------------------](ma74x.png)
Integrating over time we obtain
![∫
t 2k-
W (z,τ)= 0 − r [T (z+ V τ,τ )− Te] dτ+ g(z)](ma75x.png)
For an arbitrary function 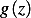 , Substituting back for
, Substituting back for 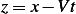 and
and 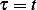 we obtain
we obtain
Hence general solution is
![|--------------------------------------------------|
| −2k∫t |
| T (x,t)= r 0[T (x+ V (τ− t),t)− Te]dτ + g(x− V t) |
----------------------------------------------------](ma80x.png)
The function 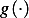 can be found from initial conditions that specific
can be found from initial conditions that specific 
2 Problem 6 page 372 section 6.3
problem:
Prove that if the Dirchlet problem
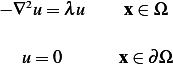
has nontrivial solution then the constant 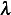 must be positive.
must be positive.
solution:
Using Green first identity,
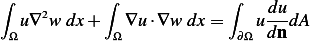
Let 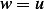 in the above
in the above
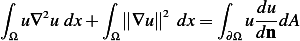
But 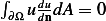 since
since 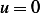 on
on 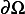 , hence
, hence
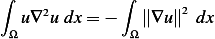
Now 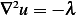 from the PDE itself, hence the above becomes
from the PDE itself, hence the above becomes
The integral in the RHS is 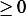
Consider the case if the integral in the RHS is zero. This implies that 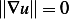 . But
. But 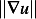 is a norm
of a vector. (this vector being the gradient of the scalar field function
is a norm
of a vector. (this vector being the gradient of the scalar field function 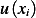 ). The only way for
a norm of a vector to be zero is for the vector itself to be zero. For example, look at
). The only way for
a norm of a vector to be zero is for the vector itself to be zero. For example, look at  ,
,
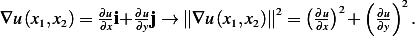 Since this sum is zero, and we are adding nonnegative
numbers, then this means
Since this sum is zero, and we are adding nonnegative
numbers, then this means 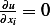 ,
, 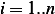 . This implies that
. This implies that  itself is either zero everywhere, or
itself is either zero everywhere, or  is not
zero, but
is not
zero, but 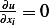 , i.e.
, i.e.  is a constant function w.r.t to each of its independent variables. But we can't use the
case when
is a constant function w.r.t to each of its independent variables. But we can't use the
case when 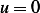 everywhere since we are looking for nontrivial solution, hence the other possibility is for
everywhere since we are looking for nontrivial solution, hence the other possibility is for  is a constant function w.r.t to each of its independent variables. But this case also fails, because we
are told
is a constant function w.r.t to each of its independent variables. But this case also fails, because we
are told 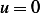 on
on 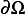 , and so if it is constant, this means it is zero also everywhere inside
, and so if it is constant, this means it is zero also everywhere inside  which means the trivial solution again, which we do not like. Hence we conclude that
which means the trivial solution again, which we do not like. Hence we conclude that 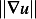 can
NOT be zero. Hence only other option is for it to be strictly positive, i.e.
can
NOT be zero. Hence only other option is for it to be strictly positive, i.e. 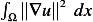 must be
must be
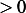
Hence 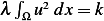 , where
, where 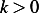 . But since
. But since  is not zero, then
is not zero, then 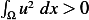 , hence
, hence
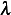 is strictly positive
is strictly positive
3 Problem 10 page 373 section 6.3
question:
solution:
Part(a)
Apply balance equation. Using the volume density of the material as the quantity to conserve. There is no
loss in this problem, hence 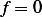
Hence
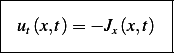
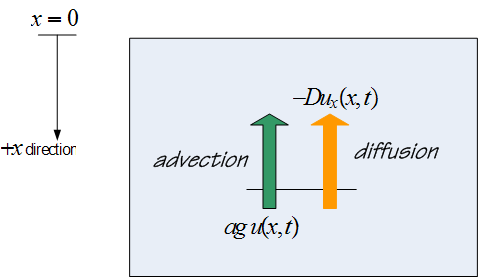
Now the flux is made up of 2 parts in this problem, due to advection and due to diffusion.
Hence
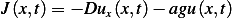
Where the minus sign next to the advection term is due to speed being in opposite direction to the x-axis.
Hence the PDE is
![∂
ut(x,t)= ---[Dux (x,t)+ agu (x,t)]
∂ x](ma123x.png)
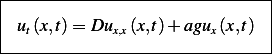
Part(b)
At steady state, 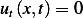 , hence we obtain
, hence we obtain
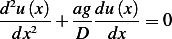
We can solve this by separation of variables. Let 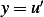
Let 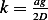 Since
Since 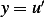
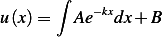
Hence
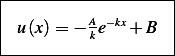
We consider that at 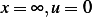 , (i.e. since very deep lake, we take
, (i.e. since very deep lake, we take 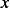 very large)
very large)
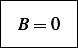
Then
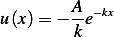
We also know that 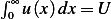 , hence
, hence
Hence 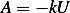
Hence the solution is
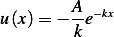
Then
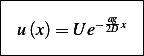
To verify, as 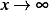 we obtain
we obtain 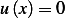 and at
and at 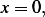
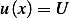
Note, it does not seem to make too much sense to me that in any tube length, total amount is always 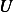 ,
for this implies, for some length
,
for this implies, for some length 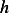 that
that 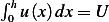 but
but ![∫ ∫ h
0hu(x)dx= 0hUe−kxdx= −Uk [e−kx]0 = −Uk[e−kh− 1]](ma149x.png)
Hence ![-U[e−kh − 1 ]= U
−k](ma150x.png) which means
which means 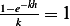 or
or 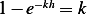 , which means
, which means 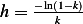 which at
which at 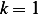 blows up. So this means
blows up. So this means 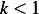 , i.e.
, i.e. 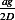 must be
must be 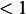 .
.
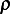 , specific heat
, specific heat  , and heat conductivity
, and heat conductivity 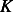 , flows at a constant velocity
, flows at a constant velocity 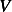 in a
cylindrical tube of length
in a
cylindrical tube of length 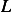 , and radius
, and radius 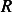 . The temperature at position
. The temperature at position 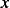 is
is 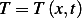 and diffusion of
heat is ignored. As it flows, heat is lost though the lateral side at a rate jointly proportional to
the area and to the difference between the temperature
and diffusion of
heat is ignored. As it flows, heat is lost though the lateral side at a rate jointly proportional to
the area and to the difference between the temperature 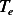 of the external environment and the
temperature
of the external environment and the
temperature 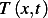 of the fluid (Newton's law of cooling). Derive a PDE model for the temperature
of the fluid (Newton's law of cooling). Derive a PDE model for the temperature
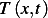
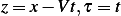
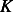
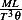

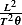
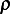
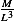
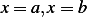 .
.
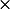 specific heat
specific heat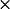 its
temperature
its
temperature 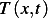
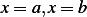 is
is
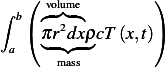
 and
and 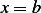 , this is given
by
, this is given
by
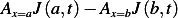
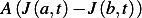
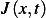 is the amount of heat that flows though a unit area per unit time. (the Flux)
is the amount of heat that flows though a unit area per unit time. (the Flux)
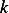 . The area of the body in this case is the surface of
the cylinder of strip of width
. The area of the body in this case is the surface of
the cylinder of strip of width 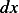 which is given by
which is given by 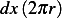 when considering a differential
length.
when considering a differential
length.
 and
and 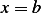 is
is ![[ ∫ b ]
− a k dx(2πr )(T (x,t)− Te)](ma36x.png) . The minus sign is
to say that this is considered to be a heat loss, not gain, into the volume under consideration. Now need to find
what the units of this
. The minus sign is
to say that this is considered to be a heat loss, not gain, into the volume under consideration. Now need to find
what the units of this 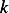 is (this is NOT the heat conductivity coefficient). Using dimensional analysis, we
write
is (this is NOT the heat conductivity coefficient). Using dimensional analysis, we
write
![[rate of heat]](ma38x.png) =
= ![[ML2]
[k][L2][𝜃]→ [k]= [rate-of-heat]= --[heat]- = ---T2- =
[L2][𝜃] [L2][𝜃][T] [L2][𝜃][T]](ma39x.png)
![-[M]--
[𝜃][T3]](ma40x.png)
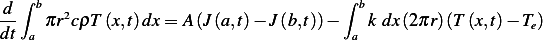
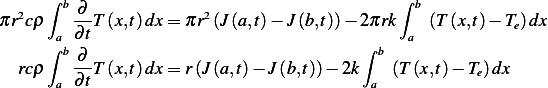
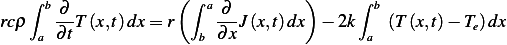
 we
obtain
we
obtain
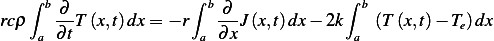
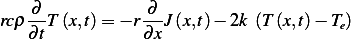
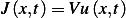 where
where 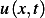 is amount of heat per unit
volume at
is amount of heat per unit
volume at 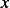 , but this is the same as
, but this is the same as 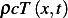 , hence
, hence 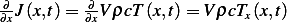 since
since 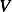 is
constant, then the above becomes
is
constant, then the above becomes
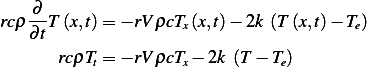
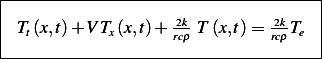
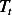 has units
has units ![[𝜃]
T](ma56x.png)
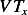 has units
has units ![[-L𝜃] [𝜃 ]
T L = T](ma58x.png)
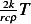 has units
has units ![[ M ]
-T32𝜃𝜃- = [-𝜃]
LTL2𝜃 ML3 T](ma60x.png)
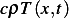 , hence rate of change of density of heat is
, hence rate of change of density of heat is 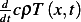
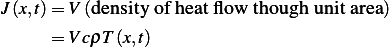
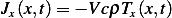
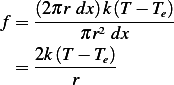
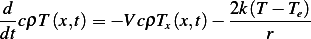
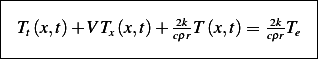
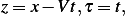 Hence
Hence
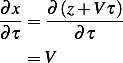
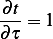
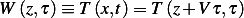 , therefore
, therefore
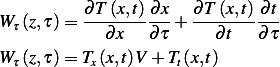
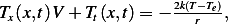 Hence
Hence
![|--------------------------------|
| W (z,τ)= − 2k[T (z+ V τ,τ )− T] |
| τ r e |
---------------------------------](ma74x.png)
![∫
t 2k-
W (z,τ)= 0 − r [T (z+ V τ,τ )− Te] dτ+ g(z)](ma75x.png)
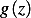 , Substituting back for
, Substituting back for 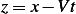 and
and 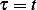 we obtain
we obtain
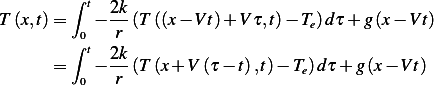
![|--------------------------------------------------|
| −2k∫t |
| T (x,t)= r 0[T (x+ V (τ− t),t)− Te]dτ + g(x− V t) |
----------------------------------------------------](ma80x.png)
 can be found from initial conditions that specific
can be found from initial conditions that specific 
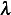 must be positive.
must be positive.
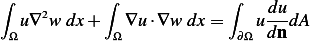
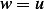 in the above
in the above
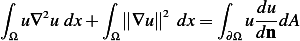
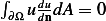
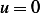 on
on 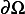 , hence
, hence
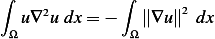
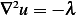 from the PDE itself, hence the above becomes
from the PDE itself, hence the above becomes
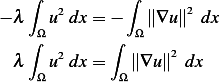
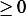
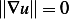 . But
. But 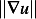 is a norm
of a vector. (this vector being the gradient of the scalar field function
is a norm
of a vector. (this vector being the gradient of the scalar field function 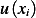 ). The only way for
a norm of a vector to be zero is for the vector itself to be zero. For example, look at
). The only way for
a norm of a vector to be zero is for the vector itself to be zero. For example, look at 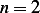 ,
,
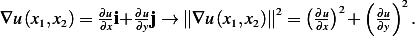 Since this sum is zero, and we are adding nonnegative
numbers, then this means
Since this sum is zero, and we are adding nonnegative
numbers, then this means 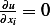 ,
, 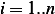 . This implies that
. This implies that  itself is either zero everywhere, or
itself is either zero everywhere, or  is not
zero, but
is not
zero, but 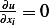 , i.e.
, i.e.  is a constant function w.r.t to each of its independent variables. But we can't use the
case when
is a constant function w.r.t to each of its independent variables. But we can't use the
case when 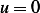 everywhere since we are looking for nontrivial solution, hence the other possibility is for
everywhere since we are looking for nontrivial solution, hence the other possibility is for  is a constant function w.r.t to each of its independent variables. But this case also fails, because we
are told
is a constant function w.r.t to each of its independent variables. But this case also fails, because we
are told 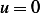 on
on 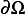 , and so if it is constant, this means it is zero also everywhere inside
, and so if it is constant, this means it is zero also everywhere inside  which means the trivial solution again, which we do not like. Hence we conclude that
which means the trivial solution again, which we do not like. Hence we conclude that 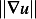 can
NOT be zero. Hence only other option is for it to be strictly positive, i.e.
can
NOT be zero. Hence only other option is for it to be strictly positive, i.e. 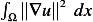 must be
must be
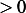
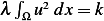 , where
, where 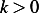 . But since
. But since  is not zero, then
is not zero, then 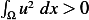 , hence
, hence
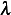 is strictly positive
is strictly positive
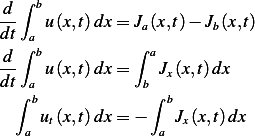
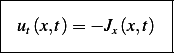
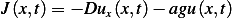
![∂
ut(x,t)= ---[Dux (x,t)+ agu (x,t)]
∂ x](ma123x.png)
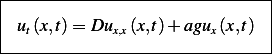
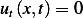 , hence we obtain
, hence we obtain
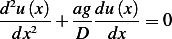
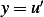
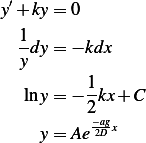
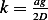 Since
Since 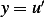
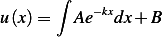
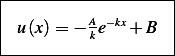
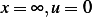 , (i.e. since very deep lake, we take
, (i.e. since very deep lake, we take 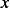 very large)
very large)
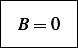
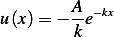
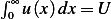 , hence
, hence
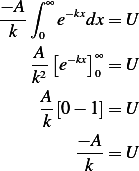
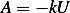
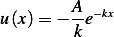
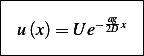
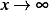 we obtain
we obtain 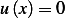 and at
and at 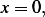
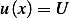
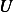 ,
for this implies, for some length
,
for this implies, for some length 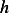 that
that 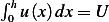 but
but ![∫ ∫ h
0hu(x)dx= 0hUe−kxdx= −Uk [e−kx]0 = −Uk[e−kh− 1]](ma149x.png)
![-U[e−kh − 1 ]= U
−k](ma150x.png) which means
which means 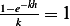 or
or 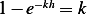 , which means
, which means 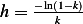 which at
which at 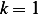 blows up. So this means
blows up. So this means 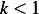 , i.e.
, i.e. 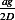 must be
must be 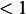 .
.