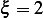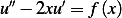 ,
,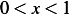 ,
, 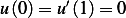 . Find Green function or
explain where there isn't one.
. Find Green function or
explain where there isn't one.
problem:
Consider boundary value problem 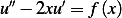 ,
,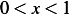 ,
, 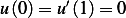 . Find Green function or
explain where there isn't one.
. Find Green function or
explain where there isn't one.
answer:
We see that 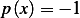
First, lets see if 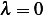 or not. Since if
or not. Since if 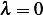 since by theorem 4.19 (page 248) Green function does not
exist, and I do not need to try to find it.
since by theorem 4.19 (page 248) Green function does not
exist, and I do not need to try to find it.
Let
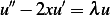
If 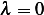 then solve the homogeneous equation
then solve the homogeneous equation 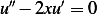 . Let
. Let 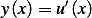 , hence we obtain
, hence we obtain
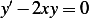 , by separation of variables, we then have
, by separation of variables, we then have
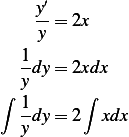
Hence
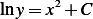
Which leads to 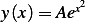 . But since
. But since 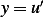 , then
, then 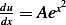 or
or
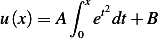
Therefore,
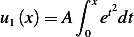
and
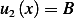
At 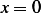 we have
we have 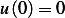 , hence
, hence 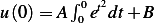 or
or 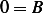 so now
so now 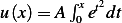 . Now lets see
if this satisfies the second boundary condition
. Now lets see
if this satisfies the second boundary condition 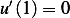 . First note that
. First note that
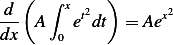
hence 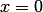 at
at 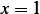 we obtain
we obtain 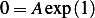 which means
which means 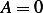 , but this means trivial solution since both
, but this means trivial solution since both 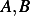 are zero. Hence
are zero. Hence 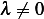 OK, so now I try to find Green function:
OK, so now I try to find Green function:
Now we need to find 2 independent solutions as combinations of 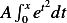 and
and 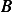 such that each will
satisfies at least one of the boundary conditions.
such that each will
satisfies at least one of the boundary conditions.
We need 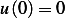 , hence if we take
, hence if we take
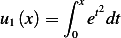
which will be zero at 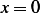 , and if we take
, and if we take
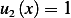
then we see that 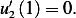 Now find the Wronskian
Now find the Wronskian
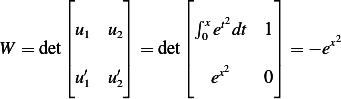
Hence using equation 4.46 we obtain, noting that 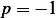
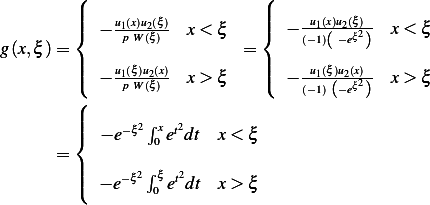
Hence
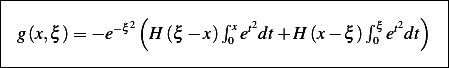
and
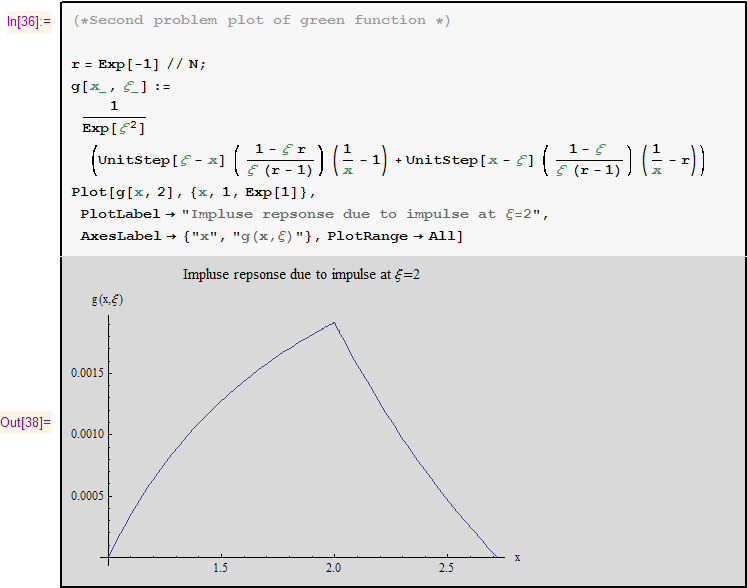
I used the Green function I derived, and used it to plot the solution (for 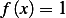 ) and compare the plot
with the analytical solution.
) and compare the plot
with the analytical solution.
This is a plot of just the impulse response (green function) due to an impulse at 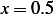
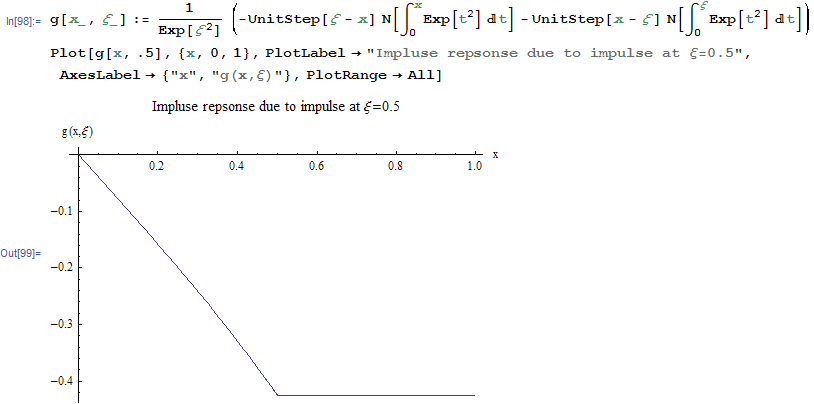
This is another method to solving this problem by using properties of Green function
From above we found 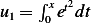 ,
, 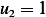 , but
, but
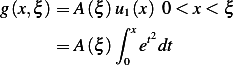
and
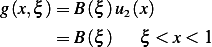
At 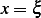 , due to continuity, we require that
, due to continuity, we require that
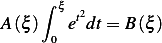 | (1) |
and to impose the discontinuity condition on the first derivative we have
From (1) we then obtain that
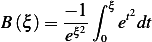
Hence
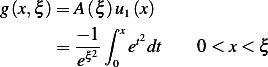
and
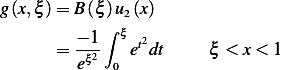
Hence
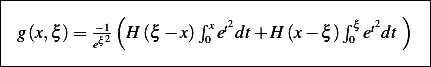
Compare this solution to the one found above using the formula method we see they are the same.
Problem:
Find the inverse of the differential operator 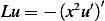 on
on 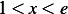 subject to
subject to 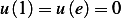
solution:
This is SLP problem with 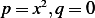 . First find if
. First find if 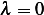 is possible eigenvalue.
is possible eigenvalue.
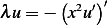
Let 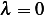 , hence we have
, hence we have 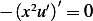 or
or 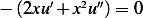 or
or
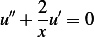
Use separation of variables. First let 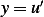 , hence
, hence 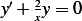 or
or 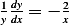 hence
hence
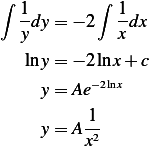
But 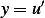 , hence
, hence 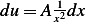 or
or 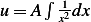
hence 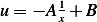 or
or
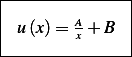
where the minus sign is absorbed into 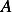 . Hence we have 2 independent solutions
. Hence we have 2 independent solutions 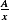 and
and 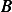 ,
so we need combination of these 2 solutions to satisfy the BV. At
,
so we need combination of these 2 solutions to satisfy the BV. At 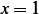 we have
we have 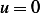 , hence
if we take
, hence
if we take 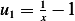 then it will satisfy this condition. At
then it will satisfy this condition. At  we need
we need 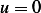 , hence take
, hence take
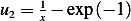
Then
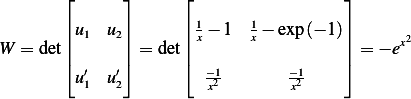
Hence
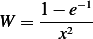
Then green function is
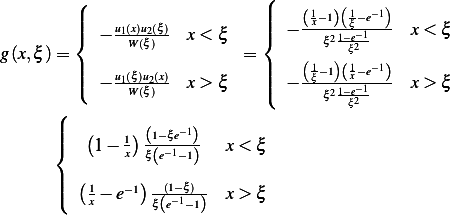
But the inverse 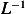 is
is 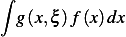 where
where 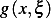 is the green function given aboive.
is the green function given aboive.
Another way to solve the problem:
From above we found 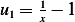 ,
, 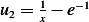 , but
, but
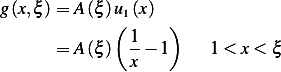
and
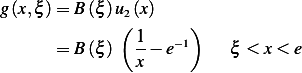
At 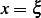 , due to continuity, we require that
, due to continuity, we require that
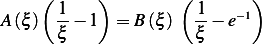 | (1) |
and to impose the discontinuity condition on the first derivative we have
Solve (1) and (2) for 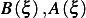
From (2) we have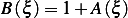
 substitute into (1) we have
substitute into (1) we have 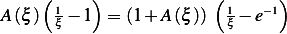 or
or
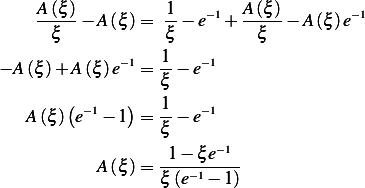
Hence
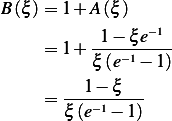
Then
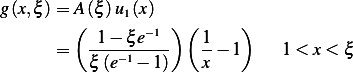
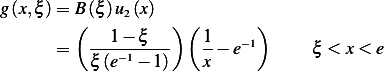
Hence
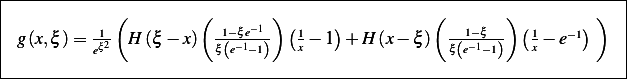
Which agree with the formula method.
This a plot of Green function for