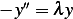 ,
, 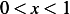 with B.V.
with B.V. 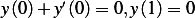
problem:
Consider SLP 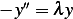 ,
, 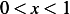 with B.V.
with B.V. 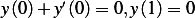
is 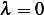 an eigenvalue? are there negative eigenvalues? show that there are infinitely many positive
eigenvalues by finding an equation whose roots are those eigenvalues and show graphically that there are
infinity many root
an eigenvalue? are there negative eigenvalues? show that there are infinitely many positive
eigenvalues by finding an equation whose roots are those eigenvalues and show graphically that there are
infinity many root
answer:
The SLP has the form 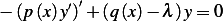 or
or 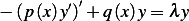 for
for  , where
, where
 not zero function and does not change sign over the interval, hence we can assume it to be positive. If we
compare this form to the given problem we see that
not zero function and does not change sign over the interval, hence we can assume it to be positive. If we
compare this form to the given problem we see that 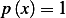 and
and 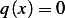
Assume 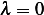 , hence the ODE become
, hence the ODE become 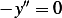 which has the solution
which has the solution 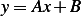 for some constants
for some constants
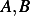 . Now lets see is this solution can satisfy the B,V, given.
. Now lets see is this solution can satisfy the B,V, given.
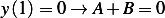 , and
, and 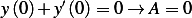 , hence since
, hence since 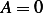 , then
, then 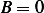 hence the only
solution is
hence the only
solution is 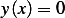 . Hence for non-trivial solution
. Hence for non-trivial solution 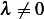
Now let us assume 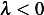 . Assume
. Assume 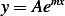 , hence the characteristic equation is
, hence the characteristic equation is 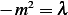 or
or 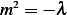 ,
but since
,
but since 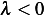 , then
, then  is a real quantity. Let
is a real quantity. Let 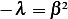 where
where 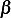 is some non zero real constant, hence we
have
is some non zero real constant, hence we
have 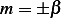 and so the solution is
and so the solution is
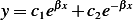
Let see is this solution will satisfy the B.V. 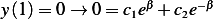 , and
, and 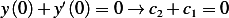 ,
hence
,
hence 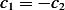 , and we have
, and we have 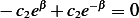 , hence
, hence 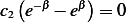 , or but
, or but 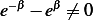 (it is
zero only if
(it is
zero only if 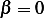 but we have that
but we have that 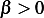 ) then this means that
) then this means that 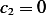 . But this means that
. But this means that
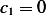 , which then means that the solution is again
, which then means that the solution is again 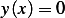 . Therefore, for non-trivial solution,
. Therefore, for non-trivial solution,
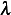 can not be negative.
can not be negative.
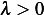
. (We do not have to check for this, since we know that 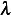 does not change sign) but for an exercise, let us
verify it any way. As above, we obtain
does not change sign) but for an exercise, let us
verify it any way. As above, we obtain 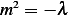 but since
but since 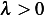 then solution will now contain complex
exponential since
then solution will now contain complex
exponential since 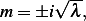 then solution is (by writing
then solution is (by writing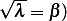
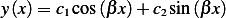
Verify B,V, The first one leads to
and the second one leads to, since 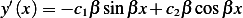 , we obtain
, we obtain
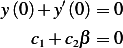
or 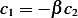 , now substitute this in the first initial condition (1) we obtain
, now substitute this in the first initial condition (1) we obtain
But if 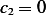 this will lead to
this will lead to 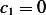 also and to a trivial solution. Hence we need to consider
also and to a trivial solution. Hence we need to consider
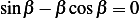 or roots of
or roots of
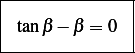
The roots are the intersection of 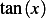 with the line
with the line 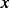 , graphically we see the roots occur close to
multiplies of
, graphically we see the roots occur close to
multiplies of 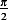
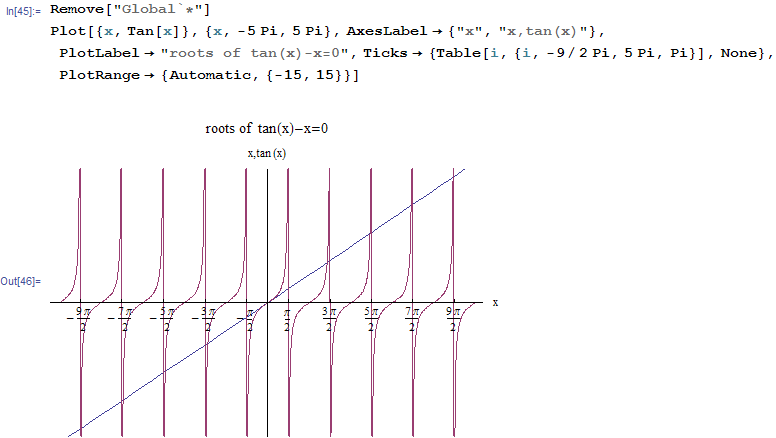
Or we can just plot the function 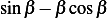
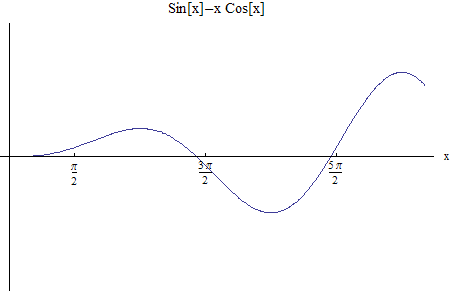
To find the roots, use a numerical root finder (Newton's method), here are the first 10 positive roots (we do
not pick the zero root, since  )
)

Hence the square of the above is the list of the eigenvalues. Here are first few
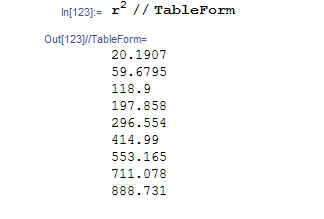
Hence the eigenfunctions are
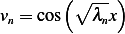
and
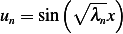
for 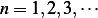 where
where 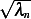 is the root of
is the root of 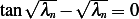 , and the first few
, and the first few 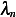 are shown
above.
are shown
above.
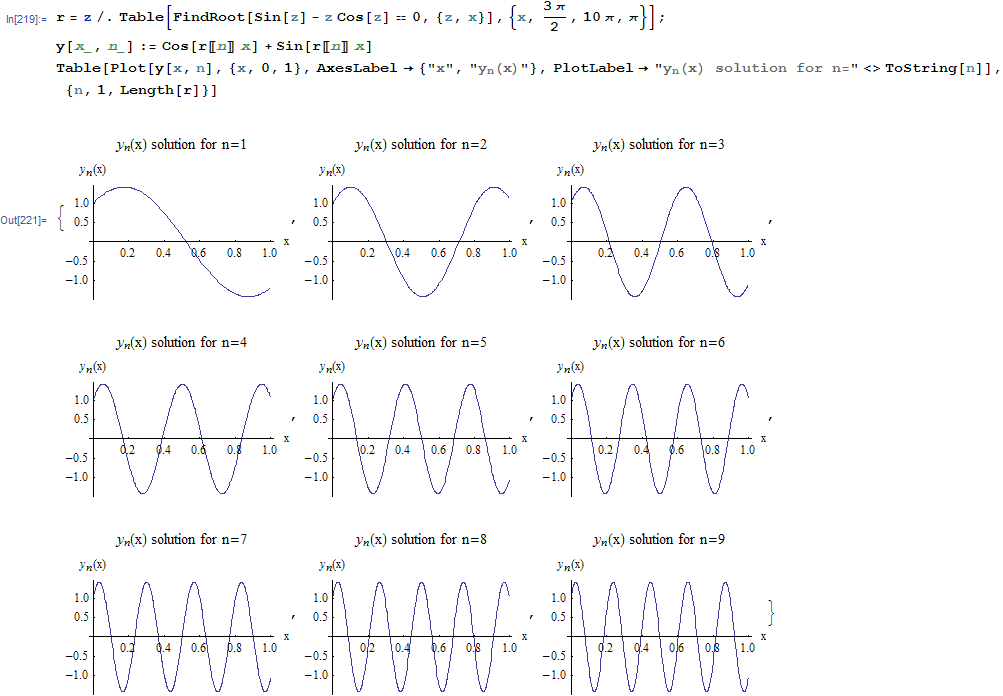
Here is a plot of few solutions for 
problem:
Find eigenvalues and eigenfunctions for the problem 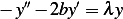 ,
, 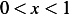
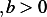 , and
, and
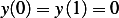
answer:
The SLP has the form 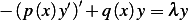 for
for 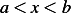 , where
, where 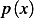 not zero function and does not
change sign over the interval, hence we can assume it to be positive. If we compare this form to the given
problem we see that
not zero function and does not
change sign over the interval, hence we can assume it to be positive. If we compare this form to the given
problem we see that 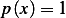 and
and 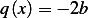 and since
and since 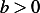 then
then 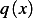 is always negative over this
range
is always negative over this
range
Assume 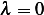 , hence the ODE become
, hence the ODE become 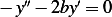 which has the characteristic equation
which has the characteristic equation
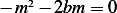 or
or 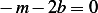 , hence
, hence 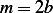 , then the solution is
, then the solution is 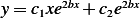 . Now from
. Now from
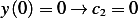 , and so
, and so 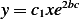 , Now from
, Now from 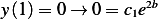 , but
, but 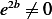 hence
hence 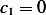 , hence we
obtain trivial solution
, hence we
obtain trivial solution 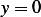 , hence for non-trivial solution
, hence for non-trivial solution 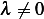 .
.
Now 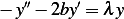 , and the characteristic equation is
, and the characteristic equation is 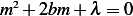 , hence
, hence 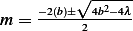 ,
hence
,
hence 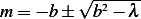 . There are 3 cases:
. There are 3 cases: 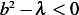 and
and 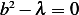 and
and 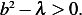
When 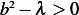 , we have
, we have  will be real. Hence the solution will be of the form
will be real. Hence the solution will be of the form 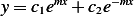 ,
where
,
where  is real. Now let see if we can satisfy the boundary conditions. From
is real. Now let see if we can satisfy the boundary conditions. From 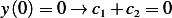 , and
from
, and
from 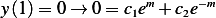 , hence
, hence 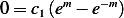 , but this means
, but this means 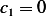 since
since  is not zero. This
leads to
is not zero. This
leads to 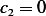 which leads to trivial solution
which leads to trivial solution 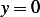 . Therefore
. Therefore 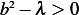 is not possible choice.
is not possible choice.
When 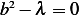 , hence
, hence 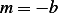 , then the solution is
, then the solution is 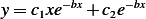 , and by similar argument as
above for the case of
, and by similar argument as
above for the case of 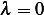 , we conclude that it is not possible to have
, we conclude that it is not possible to have 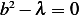
Hence 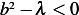 or
or 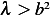
 In other words,
In other words, 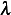 is positive and must be greater than
is positive and must be greater than 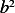 . Let
. Let
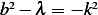 for
for 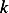 real and nonzero. Hence
real and nonzero. Hence
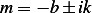
and the solution is
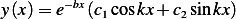
at 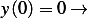
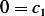 and
and 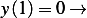
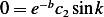
Hence for non-trivial solution,
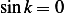
or 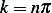 or
or 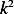
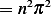 . But
. But 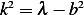 Hence
Hence 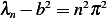 . Now since
. Now since 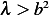 we can eliminate that
we can eliminate that
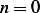 case. Then we have
case. Then we have
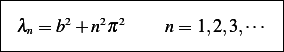
Hence 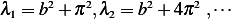
So the eigenfunctions are
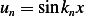
where 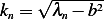
So the 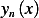 solution is
solution is
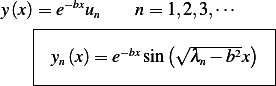
problem:
Find eigenvalues and eigenfunctions for the problem with periodic boundary conditions 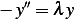 ,
,
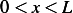 and
and 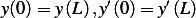
answer:
The SLP has the form 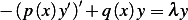 for
for 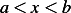 , where
, where 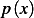 not zero function and does not
change sign over the interval, hence we can assume it to be positive. If we compare this form to the given
problem we see that
not zero function and does not
change sign over the interval, hence we can assume it to be positive. If we compare this form to the given
problem we see that 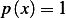 and
and 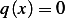
Assume 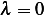 , hence we have
, hence we have 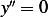 or
or 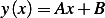 . Now to satisfy
. Now to satisfy 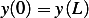 we must have
we must have
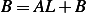 which implies
which implies 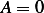 , hence
, hence 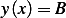 . Now this solution does satisfy
. Now this solution does satisfy 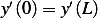 since
since
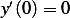 and
and 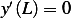 hence
hence 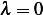 is an eigenvalue.
is an eigenvalue.
Now Assume 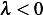 . Hence
. Hence 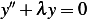 and characteristic equation is
and characteristic equation is 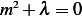 or
or 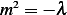 , since
, since
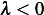 , then
, then 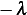 is positive, hence this leads to solution of
is positive, hence this leads to solution of 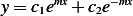 where
where  is real. Now to
satisfy
is real. Now to
satisfy 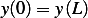 we must have
we must have
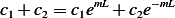 | (1) |
and to satisfy 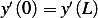 we must have, since
we must have, since 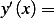
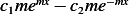 that
that
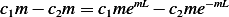 |
Since 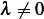 in this case, then
in this case, then 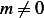 so we can divide by
so we can divide by  and obtain
and obtain
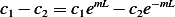 | (2) |
add (1)+(2) we have
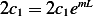 or
or 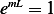 hence
hence 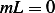 or
or 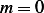 which contradicts our assumption that
which contradicts our assumption that 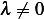 . So
. So
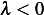 is not possible.
is not possible.
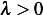
, Hence 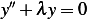 and characteristic equation is
and characteristic equation is 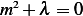 or
or 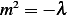 , since
, since 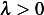 , then
, then  is
complex„ hence
is
complex„ hence 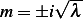 and this leads to solution of (by letting
and this leads to solution of (by letting 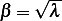 )
)
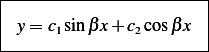
Now to satisfy 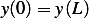 we must have
we must have
and to satisfy 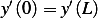 we must have, since
we must have, since
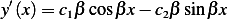
that
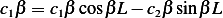 | (4) |
Substitute (3) into (4) we have
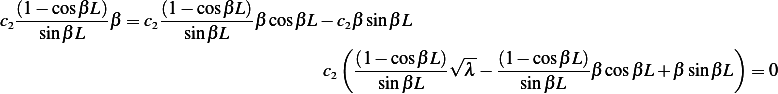 |
Since 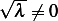 the above becomes
the above becomes
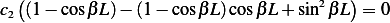
Now 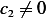 else this makes
else this makes 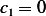 also and we obtain trivial solution. Hence we must have
also and we obtain trivial solution. Hence we must have
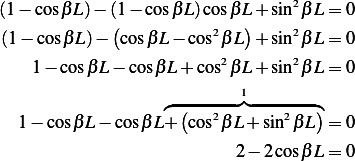
Hence
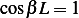
or
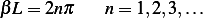
Hence
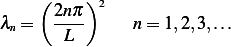
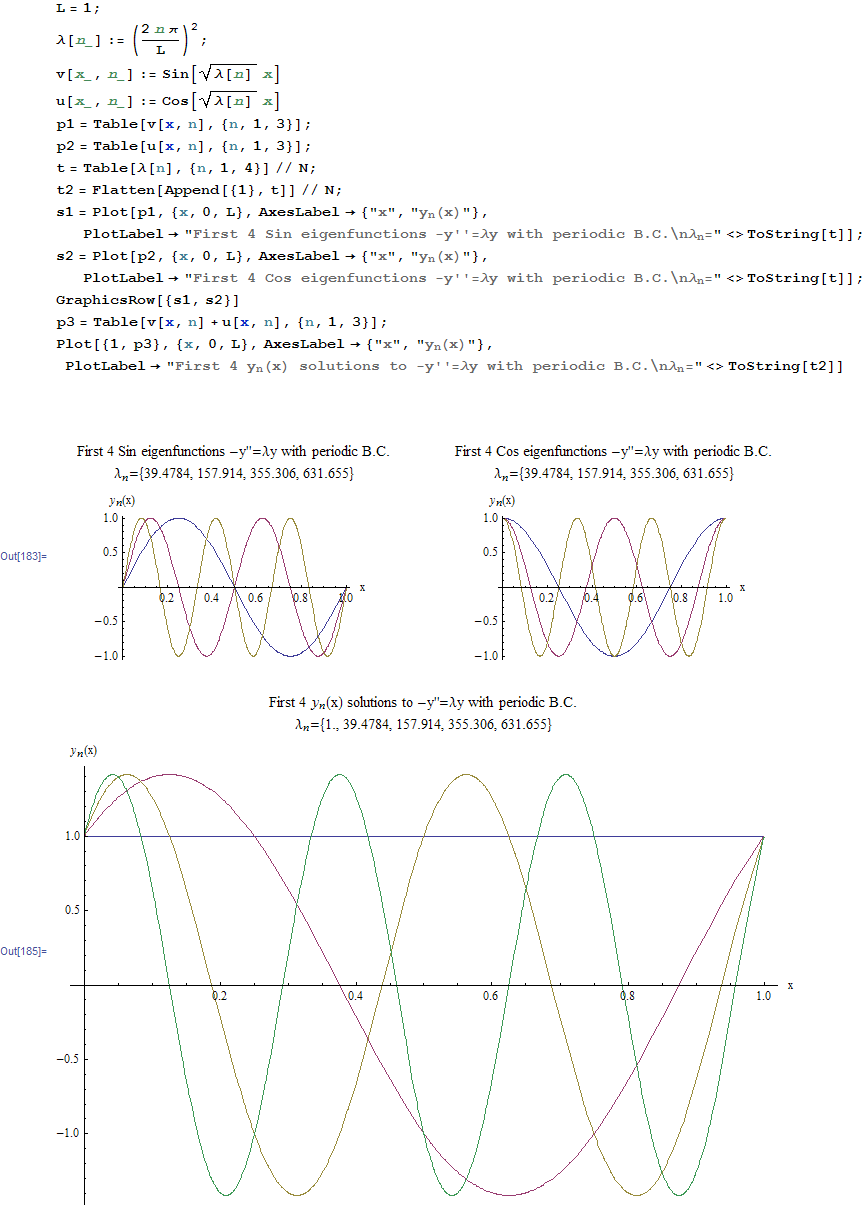
Hence the eigenfunctions are 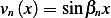 and
and 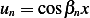
For 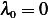 ,
, 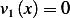 and
and 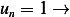
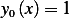
For 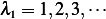
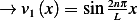 and
and 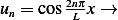
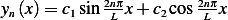
this is a plot of few eigenfunctions 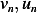 and the complete solution
and the complete solution 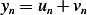 for first few
eigenvalues
for first few
eigenvalues