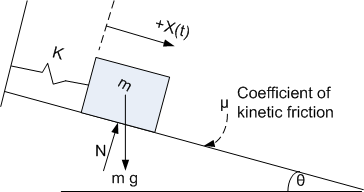
Find the equation of motion for the following system

Solution
Assume initial conditions are \(x\left ( 0\right ) =x_{0}\) and \(\dot{x}\left ( 0\right ) =0\). Assume that \(x_{0}\) was positive (i.e. to the right of the static equilibrium position, and also assume that \(kx_{0}>N\ \mu _{static}\)). This second requirement is needed to enable the mass to undergo motion by overcoming static friction. The normal force \(N\) is given by\[ N=mg\cos \theta \] And the dynamic friction force \(f_{c}\) due to the dynamic friction is defined as follows\[ f_{c}=\left \{ \begin{array} [c]{ccc}-\mu N & & \dot{x}>0\\ 0 & & \dot{x}=0\\ \mu N & & \dot{x}<0 \end{array} \right . \] But since \(N=mg\cos \theta \), then the above becomes\begin{equation} f_{c}=\left \{ \begin{array} [c]{ccc}-\mu mg\cos \theta & & \dot{x}>0\\ 0 & & \dot{x}=0\\ \mu mg\cos \theta & & \dot{x}<0 \end{array} \right . \tag{1} \end{equation} Where \(\mu \) is the coefficient of dynamic friction. Now we can obtain the Lagrangian\begin{align*} L & =T-U\\ T & =\frac{1}{2}m\dot{x}^{2}\\ U & =\frac{1}{2}kx^{2} \end{align*}
Hence \[ L=\frac{1}{2}m\dot{x}^{2}-\frac{1}{2}kx^{2}\] and\begin{align*} \frac{\partial L}{\partial \dot{x}} & =m\dot{x}\\ \frac{d}{dt}\frac{\partial L}{\partial \dot{x}} & =m\ddot{x}\\ \frac{\partial L}{\partial x} & =-kx \end{align*}
Then the EQM is\begin{align*} \frac{d}{dt}\frac{\partial L}{\partial \dot{x}}-\frac{\partial L}{\partial x} & =f_{c}\\ m\ddot{x}+kx & =f_{c} \end{align*}
Where \(f_{c}\) is given by (1). Since \(f_{c}\) sign depends in the mass is moving to the left or to the right, we will generate 2 equation of motions, one for each case.
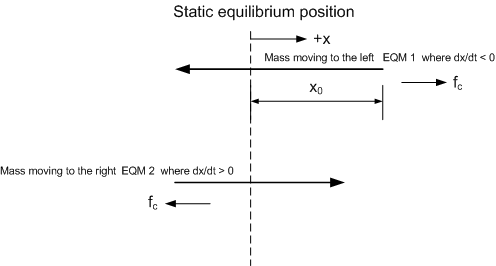
When mass is moving to the left, EQM 1 is\begin{equation} m\ddot{x}+kx=\mu mg\cos \theta \tag{2} \end{equation} When mass is moving to the right, EQM 2 is\begin{equation} m\ddot{x}+kx=-\mu mg\cos \theta \tag{3} \end{equation} So, for the first move, starting from \(x_{0}\) and moving to the left, we have\begin{align*} \ddot{x}+\frac{k}{m}x & =\mu g\cos \theta \\ \ddot{x}+\omega _{n}^{2}x & =\mu g\cos \theta \end{align*}
\[ x=x_{h}+x_{p}\] Guess \(x_{p}=X\), hence \(\omega _{n}^{2}X=\mu g\cos \theta \,\ \)or \(X=\frac{\mu g\cos \theta }{\omega _{n}^{2}}\), and \(x_{h}=A\cos \omega _{n}t+B\sin \omega _{n}t\), therefore, the solution to EQM 1 is\[ x\left ( t\right ) =A\cos \omega _{n}t+B\sin \omega _{n}t+\frac{\mu g\cos \theta }{\omega _{n}^{2}}\] \(x\left ( 0\right ) =x_{0}=A+\frac{\mu g\cos \theta }{\omega _{n}^{2}}\) hence \(A=x_{0}-\frac{\mu g\cos \theta }{\omega _{n}^{2}}\), then\[ x\left ( t\right ) =\left ( x_{0}-\frac{\mu g\cos \theta }{\omega _{n}^{2}}\right ) \cos \omega _{n}t+B\sin \omega _{n}t+\frac{\mu g\cos \theta }{\omega _{n}^{2}}\] and\begin{align*} \dot{x}\left ( t\right ) & =-\omega _{n}\left ( x_{0}-\frac{\mu g\cos \theta }{\omega _{n}^{2}}\right ) \sin \omega _{n}t+\omega _{n}B\cos \omega _{n}t\\ \dot{x}\left ( 0\right ) & =v_{0}=0=\omega _{n}B \end{align*}
Hence \(B=0\), then EQM is (for \(0<t<\frac{\pi }{\omega _{n}}\))\begin{equation} x_{left}\left ( t\right ) =\left ( x_{0}-\frac{\mu g\cos \theta }{\omega _{n}^{2}}\right ) \cos \omega _{n}t+\frac{\mu g\cos \theta }{\omega _{n}^{2}} \tag{4} \end{equation} The mass will move according to the above equation (4) until the velocity is zero, then it will turn and start moving to the right. To find the time this happens:\[ \dot{x}\left ( t\right ) =-\omega _{n}\left ( x_{0}-\frac{\mu g\cos \theta }{\omega _{n}^{2}}\right ) \sin \omega _{n}t \] Now solve for \(t\) when \(\dot{x}\left ( t\right ) =0\), i.e.,\begin{equation} 0=-\omega _{n}\left ( x_{0}-\frac{\mu g\cos \theta }{\omega _{n}^{2}}\right ) \sin \omega _{n}t \tag{5} \end{equation} Hence \(\omega _{n}t=n\pi \), where \(n=0,\pm 1,\pm 2,\cdots \)The case for \(n=0\) do not apply since this implies \(t=0\), then consider the next time this can happen, which is \(n=1\), which implies \begin{equation} t_{1}=\frac{\pi }{\omega _{n}} \tag{6} \end{equation} Now we need to determine \(x\left ( t\right ) \) at this time \(t_{1}\) since this will become the initial \(x\) for the second equation of motion going to the right in the second leg of the journey. Using (4) and (6) we obtain\begin{align*} x\left ( \frac{\pi }{\omega _{n}}\right ) & =\left ( x_{0}-\frac{\mu g\cos \theta }{\omega _{n}^{2}}\right ) \cos \omega _{n}\frac{\pi }{\omega _{n}}+\frac{\mu g\cos \theta }{\omega _{n}^{2}}\\ & =\frac{2\mu g\cos \theta }{\omega _{n}^{2}}-x_{0} \end{align*}
Notice that in the above equation, \(x_{0}\) is a positive number, since we assumed that the initial conditions \(x_{0}\) was to the right of the static equilibrium position, and we are assume the right of the static equilibrium position to be positive. This also implied that \(x\left ( \frac{\pi }{\omega _{n}}\right ) \) will be negative number (which is what we expect, as the mass will by the end of its first trip be on the left of the static equilibrium position).
Now we can use right equation of motion (EQM 2) to solve for the mass moving to the right. Notice that the initial conditions for this motion are \(x_{1}=\frac{2\mu g\cos \theta }{\omega _{n}^{2}}-x_{0}\) and \(t_{1}=\frac{\pi }{\omega _{n}}\)
The equation of motion is now\begin{align*} m\ddot{x}+kx & =-\mu mg\cos \theta \\ \ddot{x}+\omega _{n}^{2}x & =-\mu g\cos \theta \end{align*}
With the general solution\begin{equation} x\left ( t\right ) =A\cos \omega _{n}t+B\sin \omega _{n}t-\frac{\mu g\cos \theta }{\omega _{n}^{2}} \tag{7} \end{equation} At \(t=\frac{\pi }{\omega _{n}},x\left ( t\right ) =\frac{2\mu g\cos \theta }{\omega _{n}^{2}}-x_{0}\), hence from the above\begin{align*} \frac{2\mu g\cos \theta }{\omega _{n}^{2}}-x_{0} & =A\cos \omega _{n}\frac{\pi }{\omega _{n}}+B\sin \omega _{n}\frac{\pi }{\omega _{n}}-\frac{\mu g\cos \theta }{\omega _{n}^{2}}\\ & =-A-\frac{\mu g\cos \theta }{\omega _{n}^{2}}\\ A & =x_{0}-\frac{3\mu g\cos \theta }{\omega _{n}^{2}} \end{align*}
Hence (7) becomes\[ x\left ( t\right ) =\left ( x_{0}-\frac{3\mu g\cos \theta }{\omega _{n}^{2}}\right ) \cos \omega _{n}t+B\sin \omega _{n}t-\frac{\mu g\cos \theta }{\omega _{n}^{2}}\] And\[ \dot{x}\left ( t\right ) =-\omega _{n}\left ( x_{0}-\frac{3\mu g\cos \theta }{\omega _{n}^{2}}\right ) \sin \omega _{n}t+\omega _{n}B\cos \omega _{n}t \] But \(\dot{x}\left ( t\right ) =0\) at \(t=\frac{\pi }{\omega _{n}}\), hence the above becomes\begin{align*} 0 & =-\omega _{n}\left ( x_{0}-\frac{3\mu g\cos \theta }{\omega _{n}^{2}}\right ) \sin \omega _{n}\frac{\pi }{\omega _{n}}+\omega _{n}B\cos \omega _{n}\frac{\pi }{\omega _{n}}\\ & =-\omega _{n}B \end{align*}
Hence \(B=0\), then the EQM for the right move is, for \(\frac{\pi }{\omega _{n}}<t<\frac{2\pi }{\omega _{n}}\)\[ \fbox{$x_{right}\left ( t\right ) =\left ( x_{0}-\frac{3\mu g\cos \theta }{\omega _{n}^{2}}\right ) \cos \omega _{n}t-\frac{\mu g\cos \theta }{\omega _{n}^{2}}$}\] This diagram below summarize this
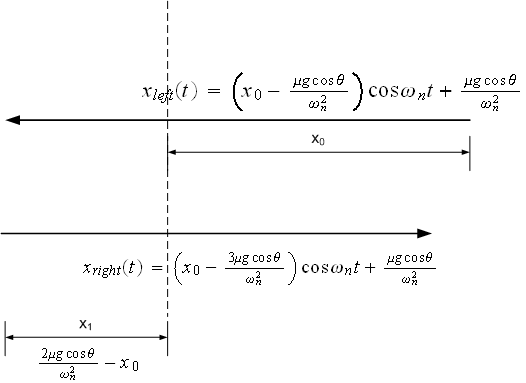
Now, we would like to have one equation to express the motion with for any time instance when the mass is moving to the left, or to the right. Looking at the above 2 equation of motion, we see immediately that we can write the equation of motion as follows\[ \fbox{$x_{n}\left ( t\right ) =\left ( x_{0}-\frac{\left ( 2n-1\right ) \mu g\cos \theta }{\omega _{n}^{2}}\right ) \cos \omega _{n}t\ +\left ( -1\right ) ^{n+1}\frac{\mu g\cos \theta }{\omega _{n}^{2}}$}\] Where \(n\) above is the number of the trip. So, the first trip, going from \(x_{0}\) and moving to the left, will have \(n=1\), and then second trip, moving from \(x_{1}\) and going to the right will have \(n=2\), and so on. As for the time during which trip travels, this is found by the following equation\[ \frac{\left ( n-1\right ) \pi }{\omega _{n}}<t_{n}<\frac{n\pi }{\omega _{n}}\] What the above is saying is that for first trip (\(n=1\)), we have\[ 0<t<\frac{\pi }{\omega _{n}}\] And for the second trip, we have\[ \frac{\pi }{\omega _{n}}<t<\frac{2\pi }{\omega _{n}}\] etc...
Now that we have one equation, and we have the time during which each equation is valid, we can now plot the equation of motion vs. time. The following is a plot for some values for \(k,g,m\). Please see the appendix for the Matlab code which generated this simulation.
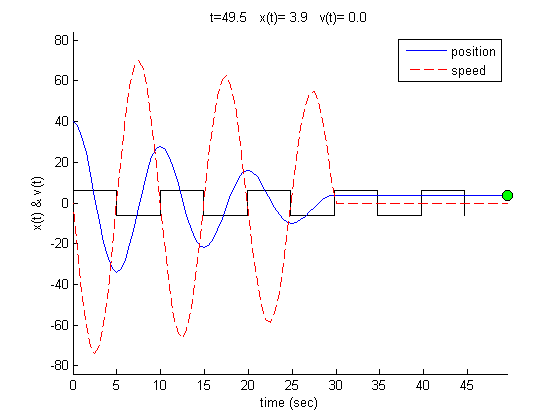
Observation found on this problem: Changing the angle of inclination \(\theta \) causes no change in results. In other words, the same oscillation will occur for flat plane (\(\theta =0\)) or for \(\theta =45^{0}\) or any other angle. The reason is because \(x_{0}\), the initial position, is measured from the static equilibrium position, and this static equilibrium position will be different as the angle changes, but the effect of the angle change is already accounted for by this change and will not be reflected in the actual displacement \(x\left ( t\right ) \).
Given \(\begin{bmatrix} 1 & 0\\ 0 & 4 \end{bmatrix} \mathbf{\ddot{X}}+\begin{bmatrix} 3 & -1\\ -1 & 1 \end{bmatrix} \mathbf{X}=\begin{bmatrix} 0\\ 0 \end{bmatrix} \) , \(m:kg,k:N/m\), use modal analysis to calculate the solution of this given \(\mathbf{X}\left ( 0\right ) =\begin{bmatrix} 0\\ 1 \end{bmatrix} mm,\ \mathbf{\dot{X}}\left ( 0\right ) =\begin{bmatrix} 0\\ 0 \end{bmatrix} mm/\sec \) also calculate the eigenvalues of the system and the normalized eigenvectors.
Answer
Since this is a 2 ODE’s that are coupled, we use modal analysis to de-couple the system first in order to obtain 2 separate ODE’s which we can then solve easily.
Let
\(M=\begin{bmatrix} 1 & 0\\ 0 & 4 \end{bmatrix} \) and let \(K=\begin{bmatrix} 3 & -1\\ -1 & 1 \end{bmatrix} \), then the above system becomes\begin{equation} M\mathbf{\ddot{X}}+K\mathbf{X}=\mathbf{0} \tag{1} \end{equation} Let \(\mathbf{X}=M^{-\frac{1}{2}}\mathbf{q}\), then \(\mathbf{\ddot{X}}=M^{-\frac{1}{2}}\mathbf{\ddot{q}}\) and the above equation becomes\[ MM^{-\frac{1}{2}}\mathbf{\ddot{q}}+KM^{-\frac{1}{2}}\mathbf{q}=\mathbf{0}\] premultiply by \(M^{-\frac{1}{2}}\) we obtain\begin{align} M^{-\frac{1}{2}}MM^{-\frac{1}{2}}\mathbf{\ddot{q}}+M^{-\frac{1}{2}}KM^{-\frac{1}{2}}\mathbf{q} & =\mathbf{0}\nonumber \\ I\mathbf{\ddot{q}}+\tilde{K}\mathbf{q} & =\mathbf{0} \tag{2} \end{align}
Where \(\tilde{K}=M^{-\frac{1}{2}}KM^{-\frac{1}{2}}\)
Let \(\mathbf{q}=\mathbf{v}e^{i\omega t}\), then \(\mathbf{\ddot{q}=-}\omega ^{2}\mathbf{v}e^{i\omega t}\) and (2) becomes\begin{align*} -\omega ^{2}e^{i\omega t}I\mathbf{v}+\tilde{K}\mathbf{v}e^{i\omega t} & =\mathbf{0}\\ \left ( \tilde{K}-\omega ^{2}I\right ) \mathbf{v} & =\mathbf{0} \end{align*}
Let \(\lambda =\omega ^{2}\) then we have\begin{equation} \left ( \tilde{K}-\lambda I\right ) \mathbf{v}=\mathbf{0} \tag{3} \end{equation} For \(\mathbf{v\neq 0\,}\), we requires that \(\left \vert \tilde{K}-\lambda I\right \vert =0\) But\begin{align*} \tilde{K} & =M^{-\frac{1}{2}}KM^{-\frac{1}{2}}\\ & =\begin{bmatrix} 1^{\frac{-1}{2}} & 0\\ 0 & 4^{\frac{-1}{2}}\end{bmatrix}\begin{bmatrix} 3 & -1\\ -1 & 1 \end{bmatrix}\begin{bmatrix} 1^{\frac{-1}{2}} & 0\\ 0 & 4^{\frac{-1}{2}}\end{bmatrix} \\ & =\begin{bmatrix} 3 & -\frac{1}{2}\\ -\frac{1}{2} & \frac{1}{4}\end{bmatrix} \end{align*}
Hence\begin{align*} \left \vert \tilde{K}-\lambda I\right \vert & =0\\ \left \vert \begin{bmatrix} 3 & -\frac{1}{2}\\ -\frac{1}{2} & \frac{1}{4}\end{bmatrix} -\lambda \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \right \vert & =0\\ \left \vert \begin{bmatrix} 3-\lambda & -\frac{1}{2}\\ -\frac{1}{2} & \frac{1}{4}-\lambda \end{bmatrix} \right \vert & =0\\ \left ( 3-\lambda \right ) \left ( \frac{1}{4}-\lambda \right ) -\frac{1}{4} & =0\\ \lambda ^{2}-\frac{13}{4}\lambda +\frac{1}{2} & =0 \end{align*}
Hence \begin{align*} \lambda & =\frac{-b}{2a}\pm \frac{\sqrt{b^{2}-4ac}}{2a}\\ & =\frac{13}{8}\pm \frac{\sqrt{\left ( \frac{13}{4}\right ) ^{2}-2}}{2}\\ & =\frac{13}{8}\pm \frac{1}{8}\sqrt{137} \end{align*}
Hence \[ \fbox{$\lambda _{1,2}=\allowbreak \left \{ \frac{13-\sqrt{137}}{8},\frac{13+\sqrt{137}}{8}\right \} =$ $\left \{ 0.161\,91,3.\,\allowbreak 088\,1\right \} $}\] From (3) we then have\begin{align*} \left ( \tilde{K}-\lambda I\right ) \mathbf{v} & =\mathbf{0}\\ \left ( \begin{bmatrix} 3 & -\frac{1}{2}\\ -\frac{1}{2} & \frac{1}{4}\end{bmatrix} -\begin{bmatrix} \lambda & 0\\ 0 & \lambda \end{bmatrix} \right ) \mathbf{v} & =\mathbf{0} \end{align*}
When \(\lambda =\lambda _{1}=0.161\,9\) we obtain\begin{align*} \left ( \begin{bmatrix} 3.0 & -0.5\\ -0.5 & 0.25 \end{bmatrix} -\begin{bmatrix} 0.161\,9 & 0\\ 0 & 0.161\,9 \end{bmatrix} \right ) \begin{bmatrix} a\\ b \end{bmatrix} & =\begin{bmatrix} 0\\ 0 \end{bmatrix} \\\begin{bmatrix} 2.\,\allowbreak 838\,1 & -0.5\\ -0.5 & 0.088\,1 \end{bmatrix}\begin{bmatrix} a\\ b \end{bmatrix} & =\begin{bmatrix} 0\\ 0 \end{bmatrix} \end{align*}
Hence \begin{align*} 2.\,\allowbreak 838\,1a-0.5b & =0\\ -0.5a-0.094\,1b & =0 \end{align*}
Let \(a=1\), then \(b=\frac{-2.\,\allowbreak 838\,1}{-0.5}=\allowbreak 5.\,\allowbreak 676\,2\), hence the second eigenvector is\[ \mathbf{v}_{1}=\begin{bmatrix} 1\\ 5.\,\allowbreak 676\,2 \end{bmatrix} \] \(\left \Vert \mathbf{v}_{1}\right \Vert =\sqrt{1+5.\,\allowbreak 676\,2^{2}}=\allowbreak 5.\,\allowbreak 763\,6\), hence normalized \(\mathbf{v}_{1}\) is\begin{align*} \mathbf{v}_{1} & =\frac{1}{\allowbreak 5.\,\allowbreak 763\,6}\begin{bmatrix} 1\\ 5.\,\allowbreak 676\,2 \end{bmatrix} \\ & \fbox{$\mathbf{v}_{1}=\begin{bmatrix} 0.173\,5\\ 0.984\,84 \end{bmatrix} $} \end{align*}
When \(\lambda =\lambda _{2}=3.\,\allowbreak 088\,1\) we obtain\begin{align*} \left ( \begin{bmatrix} 3.0 & -0.5\\ -0.5 & 0.25 \end{bmatrix} -\begin{bmatrix} 3.\,\allowbreak 088\,1 & 0\\ 0 & 3.\,\allowbreak 088\,1 \end{bmatrix} \right ) \begin{bmatrix} a\\ b \end{bmatrix} & =\begin{bmatrix} 0\\ 0 \end{bmatrix} \\\begin{bmatrix} -0.088\,1 & -0.5\\ -0.5 & -2.\,\allowbreak 838\,1 \end{bmatrix}\begin{bmatrix} a\\ b \end{bmatrix} & =\begin{bmatrix} 0\\ 0 \end{bmatrix} \end{align*}
Hence \begin{align*} -0.088\,1a-0.5b & =0\\ -0.5a-2.\,\allowbreak 838\,1b & =0 \end{align*}
Let \(a=1\) in the first equation above, then \(b=\frac{-0.088\,1}{0.5}=\allowbreak -0.176\,2\), hence the first eigenvector is\[ \mathbf{v}_{2}=\begin{bmatrix} 1\\ -0.176\,2 \end{bmatrix} \] \(\left \Vert \mathbf{v}_{2}\right \Vert =\sqrt{1+0.176\,2^{2}}=\allowbreak 1.\,\allowbreak 015\,4\), hence normalized \(\mathbf{v}_{2}\) is\begin{align*} \mathbf{v}_{2} & =\frac{1}{\allowbreak 1.\,\allowbreak 015\,4}\begin{bmatrix} 1\\ -0.176\,2 \end{bmatrix} \\ & \fbox{$\mathbf{v}_{2}=\begin{bmatrix} 0.984\,83\\ -0.173\,53 \end{bmatrix} $} \end{align*}
Then the \(P\) matrix\begin{align*} \left [ P\right ] & =\begin{bmatrix} \mathbf{v}_{1} & \mathbf{v}_{2}\end{bmatrix} \\ & =\fbox{$\begin{bmatrix} 0.173\,5 & 0.984\,83\\ 0.984\,84 & -0.173\,53 \end{bmatrix} $} \end{align*}
Now let \(\mathbf{q}=P\mathbf{r\,,}\) then equation (2) above becomes\begin{align*} I\mathbf{\ddot{q}}+\tilde{K}\mathbf{q} & =\mathbf{0}\\ IP\mathbf{\ddot{r}}+\tilde{K}P\mathbf{r} & =\mathbf{0} \end{align*}
Premultiply by \(P^{T}\)\begin{align*} P^{T}IP\mathbf{\ddot{r}}+P^{T}\tilde{K}P\mathbf{r} & =\mathbf{0}\\ I\mathbf{\ddot{r}+}P^{T}\tilde{K}P\mathbf{r} & =\mathbf{0} \end{align*}
Let \(\Lambda =P^{T}\tilde{K}P\) then the above becomes\begin{equation} I\mathbf{\ddot{r}+}\Lambda \mathbf{r}=\mathbf{0} \tag{4} \end{equation} Now find \(\Lambda \footnote{This can also be found more quickly by noting that $\Lambda =diag(\lambda _{1},\lambda _{2})$}\)\begin{align*} \Lambda & =P^{T}\tilde{K}P\\ & =\begin{bmatrix} 0.173\,5 & 0.984\,83\\ 0.984\,84 & -0.173\,53 \end{bmatrix} ^{T}\begin{bmatrix} 3.0 & -0.5\\ -0.5 & 0.25 \end{bmatrix}\begin{bmatrix} 0.173\,5 & 0.984\,83\\ 0.984\,84 & -0.173\,53 \end{bmatrix} \\ & =\fbox{$\begin{bmatrix} 0.161\,91 & 0\\ 0 & 3.\,\allowbreak 088\,1 \end{bmatrix} $} \end{align*}
\(\allowbreak \)Hence (4) becomes\[ I\mathbf{\ddot{r}}+\begin{bmatrix} 0.161\,91 & 0\\ 0 & 3.\,\allowbreak 088\,1 \end{bmatrix} \mathbf{r}=\mathbf{0}\] Which can be written as 2 equations\[\begin{bmatrix} \ddot{r}_{1}\\ \ddot{r}_{2}\end{bmatrix} +\begin{bmatrix} 0.161\,91r_{1}\\ 3.\,\allowbreak 088\,1r_{2}\end{bmatrix} =\begin{bmatrix} 0\\ 0 \end{bmatrix} \] or\begin{align} \ddot{r}_{1}+0.161\,91r_{1} & =0\tag{5}\\ \ddot{r}_{2}+3.\,\allowbreak 088\,1r_{2} & =0\nonumber \end{align}
With IC given as \[ \mathbf{X}\left ( 0\right ) =\begin{bmatrix} 0\\ 1 \end{bmatrix} \] and\(\ \)\[ \mathbf{\dot{X}}\left ( 0\right ) =\begin{bmatrix} 0\\ 0 \end{bmatrix} \] Now \(\textbf{X=}M^-\frac{1}{2}\textbf{q}\) and \(\textbf{q=}P\textbf{r}\), hence \(\textbf{X=}M^-\frac{1}{2}P\textbf{r}\), then
\begin{align*} \mathbf{r}\left ( 0\right ) & =P^{T}M^{\frac{1}{2}}\mathbf{X}\left ( 0\right ) \\\begin{bmatrix} r_{1}\left ( 0\right ) \\ r_{2}\left ( 0\right ) \end{bmatrix} & =\begin{bmatrix} 0.173\,5 & 0.984\,83\\ 0.984\,84 & -0.173\,53 \end{bmatrix} ^{T}\begin{bmatrix} 1 & 0\\ 0 & 2 \end{bmatrix}\begin{bmatrix} 0\\ 1 \end{bmatrix} \\\begin{bmatrix} r_{1}\left ( 0\right ) \\ r_{2}\left ( 0\right ) \end{bmatrix} & =\begin{bmatrix} 1.\,\allowbreak 969\,7\\ -0.347\,06 \end{bmatrix} \end{align*}
now need to find \(\mathbf{\ddot{r}}\left ( 0\right ) ,\)but since \(\mathbf{\ddot{X}}\left ( 0\right ) =\mathbf{0}\), then \(\mathbf{\ddot{r}}\left ( 0\right ) =\mathbf{0}\) as well.
Now we can solve for \(r_{1}\left ( t\right ) \) and \(r_{2}\left ( t\right ) \) since we have the IC. From (5) above \begin{align*} \ddot{r}_{1}+0.161\,91r_{1} & =0\\ r_{1}\left ( t\right ) & =A\cos \omega _{n_{1}}t+B\sin \omega _{n_{1}}t \end{align*}
At \(t=0,r_{1}\left ( 0\right ) =1.\,\allowbreak 969\,6\), hence \(1.\,\allowbreak 969\,6=A\), then\begin{align*} r_{1}\left ( t\right ) & =1.\,\allowbreak 969\,6\cos \omega _{n_{1}}t+B\sin \omega _{n_{1}}t\\ \dot{r}_{1}\left ( t\right ) & =-1.\,\allowbreak 969\,6\omega _{n_{1}}\sin \omega _{n_{1}}t+\omega _{n1}B\cos \omega _{n_{1}}t \end{align*}
At \(t=0\)\[ \dot{r}_{1}\left ( t\right ) =0=\omega _{n_{1}}B \] Hence \(B=0\), then \[ r_{1}\left ( t\right ) =1.\,\allowbreak 969\,6\cos \omega _{n_{1}}t \] But \(\omega _{n_{1}}=\sqrt{0.161\,91}=\allowbreak 0.402\,38\), hence\[ \fbox{$r_{1}\left ( t\right ) =1.\,\allowbreak 969\,6\cos \left ( 0.402\,38t\right ) $}\] Similarly we find \(r_{2}\left ( t\right ) \)\begin{align*} \ddot{r}_{2}+3.\,\allowbreak 088\,1r_{2} & =0\\ r_{2}\left ( t\right ) & =A\cos \omega _{n_{2}}t+B\sin \omega _{n_{2}}t \end{align*}
At \(t=0,r_{2}\left ( 0\right ) =-0.346\,98\), hence \(-0.346\,98=A\), then\begin{align*} r_{2}\left ( t\right ) & =-0.346\,98\cos \omega _{n_{2}}t+B\sin \omega _{n_{2}}t\\ \dot{r}_{2}\left ( t\right ) & =0.346\,98\omega _{n_{2}}\sin \omega _{n_{2}}t+\omega _{n_{2}}B\cos \omega _{n_{2}}t \end{align*}
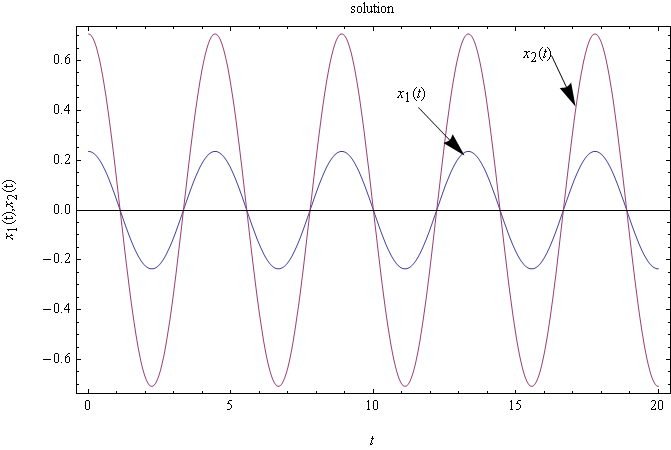
At \(t=0\)\[ \dot{r}_{2}\left ( t\right ) =0=\omega _{n_{2}}B \] Hence \(B=0\), then \[ r_{2}\left ( t\right ) =-0.346\,98\cos \omega _{n_{2}}t \] But \(\omega _{n_{2}}=\sqrt{3.\,\allowbreak 088\,1}=\allowbreak 1.\,\allowbreak 757\,3\), hence\[ \fbox{$r_{2}\left ( t\right ) =-0.346\,98\cos \left ( 1.\,\allowbreak 757\,3t\right ) $}\] Now that we found the solution in the \(r\) space, we switch back to the original \(x\) space\[ \mathbf{X}\left ( t\right ) \mathbf{=}M^{-\frac{1}{2}}P\mathbf{r}\left ( t\right ) \] Then \[ \mathbf{X}\left ( t\right ) \mathbf{=}\begin{bmatrix} 1 & 0\\ 0 & 0.5 \end{bmatrix}\begin{bmatrix} 0.173\,5 & 0.984\,83\\ 0.984\,84 & -0.173\,53 \end{bmatrix}\begin{bmatrix} 1.\,\allowbreak 969\,6\cos \left ( 0.402\,38t\right ) \\ -0.346\,98\cos \left ( 1.\,\allowbreak 757\,3t\right ) \end{bmatrix} \] \(\allowbreak \) \(\allowbreak \)Hence \[ \fbox{$\begin{bmatrix} x_{1}\left ( t\right ) \\ x_{2}\left ( t\right ) \end{bmatrix} =\begin{bmatrix} 0.341\,73\cos 0.402\,38t-0.341\,72\cos 1.\,\allowbreak 757\,3t\\ 0.969\,87\cos 0.402\,38t+0.03010\,6\cos 1.\,\allowbreak 757\,3t \end{bmatrix} $}\] This is a plot of the solutions
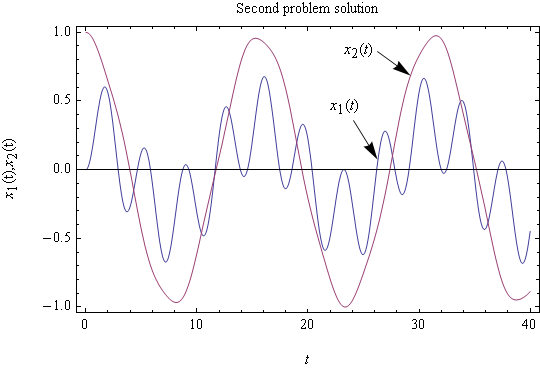
Observation on final result: Notice that power of the harmonic \(\omega _{n}=1.\,\allowbreak 757\,3\) rad/sec. in the motion \(x_{2}\left ( t\right ) \) is small (amplitude is only \(0.03\)) hence the dominant harmonic present in \(x_{2}\left ( t\right ) \) is \(\omega _{n}=0.402\,38\) rad/sec. and this reflects in the plot where it appears that \(x_{2}\left ( t\right ) \) contain one harmonic. In the case of \(x_{1}\left ( t\right ) \) we see from the solution that both frequencies contribute equal amount of power, hence the plot for \(x_{1}\left ( t\right ) \) reflects this.
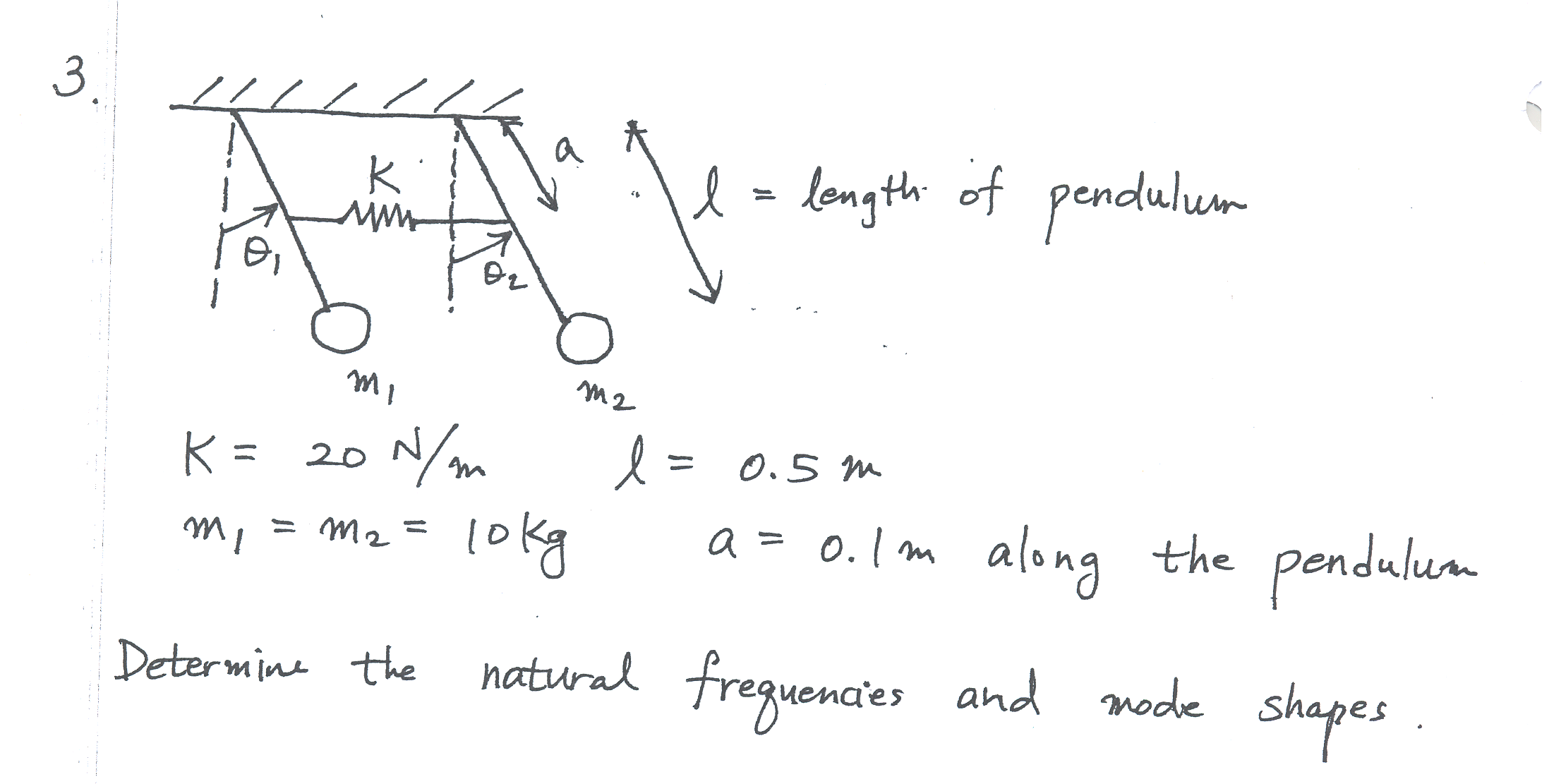
Solution Use as generalized coordinates \(\theta _{1},\theta _{2}\),. Assume that the spring remain horizontal, and assume that \(\theta _{2}>\theta _{1}\)\begin{align*} L & =T-U\\ T & =\frac{1}{2}m_{1}\left ( L\dot{\theta }_{1}\right ) ^{2}+\frac{1}{2}m_{2}\left ( L\dot{\theta }_{2}\right ) ^{2}\\ U_{gravity} & =m_{1}gL\left ( 1-\cos \theta _{1}\right ) +m_{2}gL\left ( 1-\cos \theta _{2}\right ) \\ U_{spring} & =\frac{1}{2}k\left ( a\sin \theta _{2}-a\sin \theta _{1}\right ) ^{2} \end{align*}
Hence\[ L=\frac{1}{2}m_{1}\left ( L\dot{\theta }_{1}\right ) ^{2}+\frac{1}{2}m_{2}\left ( L\dot{\theta }_{2}\right ) ^{2}-\left ( m_{1}gL\left ( 1-\cos \theta _{1}\right ) +m_{2}gL\left ( 1-\cos \theta _{2}\right ) +\frac{1}{2}k\left ( a\sin \theta _{2}-a\sin \theta _{1}\right ) ^{2}\right ) \] Now determine the Lagrangian equation\begin{align*} \frac{\partial L}{\partial \dot{\theta }_{1}} & =m_{1}L^{2}\dot{\theta }_{1}\\ \frac{d}{dt}\frac{\partial L}{\partial \dot{\theta }_{1}} & =m_{1}L^{2}\ddot{\theta }_{1}\\ \frac{\partial L}{\partial \dot{\theta }_{2}} & =m_{2}L^{2}\dot{\theta }_{2}\\ \frac{d}{dt}\frac{\partial L}{\partial \dot{\theta }_{2}} & =m_{2}L^{2}\ddot{\theta }_{2}\\ \frac{\partial L}{\partial \theta _{1}} & =-m_{1}gL\sin \theta _{1}+ak\left ( a\sin \theta _{2}-a\sin \theta _{1}\right ) \cos \theta _{1}\\ \frac{\partial L}{\partial \theta _{2}} & =-m_{1}gL\sin \theta _{2}-ak\left ( a\sin \theta _{2}-a\sin \theta _{1}\right ) \cos \theta _{2} \end{align*}
Hence the EQM for \(m_{1}\) is\begin{align*} \frac{d}{dt}\frac{\partial L}{\partial \dot{\theta }_{1}}-\frac{\partial L}{\partial \theta _{1}} & =0\\ m_{1}L^{2}\ddot{\theta }_{1}+m_{1}gL\sin \theta _{1}-ak\left ( a\sin \theta _{2}-a\sin \theta _{1}\right ) \cos \theta _{1} & =0 \end{align*}
Now apply small angle approximation. \(\sin \theta \approx \theta \) and \(\cos \theta \approx 1\)hence\begin{align*} m_{1}L^{2}\ddot{\theta }_{1}+m_{1}gL\theta _{1}-ak\left ( a\theta _{2}-a\theta _{1}\right ) & =0\\ m_{1}L^{2}\ddot{\theta }_{1}+m_{1}gL\theta _{1}-a^{2}k\theta _{2}+a^{2}k\theta _{1} & =0 \end{align*}
\begin{equation} m_{1}L^{2}\ddot{\theta }_{1}+\left ( m_{1}gL+a^{2}k\right ) \theta _{1}-a^{2}k\theta _{2}=0 \tag{1} \end{equation} And the EQM for \(m_{2}\) is\begin{align*} \frac{d}{dt}\frac{\partial L}{\partial \dot{\theta }_{2}}-\frac{\partial L}{\partial \theta _{2}} & =0\\ m_{2}L^{2}\dot{\theta }_{2}+m_{1}gL\sin \theta _{2}+ak\left ( a\sin \theta _{2}-a\sin \theta _{1}\right ) \cos \theta _{2} & =0 \end{align*}
Now apply small angle approximation. \(\sin \theta \approx \theta \) and \(\cos \theta \approx 1\)hence\begin{align*} m_{2}L^{2}\dot{\theta }_{2}+m_{1}gL\theta _{2}+ak\left ( a\theta _{2}-a\theta _{1}\right ) & =0\\ m_{2}L^{2}\dot{\theta }_{2}+m_{1}gL\theta _{2}+a^{2}k\theta _{2}-a^{2}k\theta _{1} & =0 \end{align*}
Therefore\begin{equation} m_{2}L^{2}\ddot{\theta }_{2}+\theta _{2}\left ( m_{2}gL+a^{2}k\right ) -a^{2}k\theta _{1}=0 \nonumber \end{equation} Now we write the system as \(M\mathbf{\ddot{\theta }}+K\mathbf{\theta }=0\)\[\begin{bmatrix} m_{1}L^{2} & 0\\ 0 & m_{2}L^{2}\end{bmatrix}\begin{bmatrix} \ddot{\theta }_{1}\\ \ddot{\theta }_{2}\end{bmatrix} +\begin{bmatrix} m_{1}gL+a^{2}k & -a^{2}k\\ -a^{2}k & m_{2}gL+a^{2}k \end{bmatrix}\begin{bmatrix} \theta _{1}\\ \theta _{2}\end{bmatrix} =\begin{bmatrix} 0\\ 0 \end{bmatrix} \] Substitute numerical values for the above quantities, we obtain\begin{align*} \begin{bmatrix} 10\times 0.5^{2} & 0\\ 0 & 10\times 0.5^{2}\end{bmatrix}\begin{bmatrix} \ddot{\theta }_{1}\\ \ddot{\theta }_{2}\end{bmatrix} +\begin{bmatrix} 10\times 9.8\times 0.5+0.1^{2}\times 20 & -a^{2}\times 20\\ -0.1^{2}\times 20 & 10\times 9.8\times 0.5+0.1^{2}\times 20 \end{bmatrix}\begin{bmatrix} \theta _{1}\\ \theta _{2}\end{bmatrix} & =\begin{bmatrix} 0\\ 0 \end{bmatrix} \\\begin{bmatrix} 2.\,\allowbreak 5 & 0\\ 0 & 2.\,\allowbreak 5 \end{bmatrix}\begin{bmatrix} \ddot{\theta }_{1}\\ \ddot{\theta }_{2}\end{bmatrix} +\begin{bmatrix} 49.\,\allowbreak 2 & -0.2\\ -0.2 & 49.\,\allowbreak 2 \end{bmatrix}\begin{bmatrix} \theta _{1}\\ \theta _{2}\end{bmatrix} & =\begin{bmatrix} 0\\ 0 \end{bmatrix} \end{align*}
The above can be written as\[ M\mathbf{\ddot{\theta }+}K\mathbf{\theta =0}\] Let \(\mathbf{\theta }=M^{-\frac{1}{2}}\mathbf{q}\), then \(\mathbf{\ddot{\theta }}=M^{-\frac{1}{2}}\mathbf{\ddot{q}}\) and the above equation becomes\[ MM^{-\frac{1}{2}}\mathbf{\ddot{\theta }}+KM^{-\frac{1}{2}}\mathbf{\theta }=\mathbf{0}\] premultiply by \(M^{-\frac{1}{2}}\) we obtain\begin{align} M^{-\frac{1}{2}}MM^{-\frac{1}{2}}\mathbf{\ddot{\theta }}+M^{-\frac{1}{2}}KM^{-\frac{1}{2}}\mathbf{\theta } & =\mathbf{0}\nonumber \\ I\mathbf{\ddot{\theta }}+\tilde{K}\mathbf{\theta } & =\mathbf{0} \tag{2} \end{align}
Where \(\tilde{K}=M^{-\frac{1}{2}}KM^{-\frac{1}{2}}\)
Let \(\mathbf{q}=\mathbf{v}e^{i\omega t}\), then \(\mathbf{\ddot{q}=-}\omega ^{2}\mathbf{v}e^{i\omega t}\) and (2) becomes\begin{align*} -\omega ^{2}e^{i\omega t}I\mathbf{v}+\tilde{K}\mathbf{v}e^{i\omega t} & =\mathbf{0}\\ \left ( \tilde{K}-\omega ^{2}I\right ) \mathbf{v} & =\mathbf{0} \end{align*}
Let \(\lambda =\omega ^{2}\) then we have\begin{equation} \left ( \tilde{K}-\lambda I\right ) \mathbf{v}=\mathbf{0} \tag{3} \end{equation} For \(\mathbf{v\neq 0\,}\), we requires that \(\left \vert \tilde{K}-\lambda I\right \vert =0\) But\begin{align*} \tilde{K} & =M^{-\frac{1}{2}}KM^{-\frac{1}{2}}\\ & =\begin{bmatrix} 2.\,\allowbreak 5^{-\frac{1}{2}} & 0\\ 0 & 2.\,\allowbreak 5^{-\frac{1}{2}}\end{bmatrix}\begin{bmatrix} 49.\,\allowbreak 2 & -0.2\\ -0.2 & 49.\,\allowbreak 2 \end{bmatrix}\begin{bmatrix} 2.\,\allowbreak 5^{-\frac{1}{2}} & 0\\ 0 & 2.\,\allowbreak 5^{-\frac{1}{2}}\end{bmatrix} \\ & =\fbox{$\begin{bmatrix} 19.\,\allowbreak 68 & -0.08\\ -0.08 & 19.\,\allowbreak 68 \end{bmatrix} $} \end{align*}
Hence\begin{align*} \left \vert \tilde{K}-\lambda I\right \vert & =0\\ \left \vert \begin{bmatrix} 19.\,\allowbreak 68 & -0.08\\ -0.08 & 19.\,\allowbreak 68 \end{bmatrix} -\lambda \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \right \vert & =0\\ \left \vert \begin{bmatrix} 19.\,\allowbreak 68-\lambda & -0.08\\ -0.08 & 19.\,\allowbreak 68-\lambda \end{bmatrix} \right \vert & =0\\ \left ( 19.\,\allowbreak 68-\lambda \right ) \left ( 19.\,\allowbreak 68-\lambda \right ) -0.08^{2} & =0 \end{align*}
Hence the characteristic equation is\[ \fbox{$\lambda ^{2}-39.\,\allowbreak 36\ \lambda +387.\,\allowbreak 30=0\allowbreak $}\] Hence \[ \fbox{$\lambda _{1,2}=\allowbreak 19.\,\allowbreak 6,\allowbreak 19.\,\allowbreak 76$}\] Hence the natural frequencies are\begin{align*} \omega _{n} & =\allowbreak \left \{ \sqrt{19.\,\allowbreak 6},\allowbreak \sqrt{19.\,\allowbreak 76}\right \} \\ & =\fbox{$\left \{ 4.\,\allowbreak 427\,2,4.\,\allowbreak 445\,2\right \} $ rad/sec} \end{align*}
From (3) we then have\begin{align*} \left ( \tilde{K}-\lambda I\right ) \mathbf{v} & =\mathbf{0}\\ \left ( \begin{bmatrix} 19.\,\allowbreak 68 & -0.08\\ -0.08 & 19.\,\allowbreak 68 \end{bmatrix} -\begin{bmatrix} \lambda & 0\\ 0 & \lambda \end{bmatrix} \right ) \mathbf{v} & =\mathbf{0} \end{align*}
When \(\lambda =\lambda _{1}=19.\,\allowbreak 6\) we obtain\begin{align*} \left ( \begin{bmatrix} 19.\,\allowbreak 68 & -0.08\\ -0.08 & 19.\,\allowbreak 68 \end{bmatrix} -\begin{bmatrix} 19.\,\allowbreak 6 & 0\\ 0 & 19.\,\allowbreak 6 \end{bmatrix} \right ) \begin{bmatrix} a\\ b \end{bmatrix} & =\begin{bmatrix} 0\\ 0 \end{bmatrix} \\\begin{bmatrix} 0.08 & -0.08\\ -0.08 & 0.08 \end{bmatrix}\begin{bmatrix} a\\ b \end{bmatrix} & =\begin{bmatrix} 0\\ 0 \end{bmatrix} \end{align*}
Hence \begin{align*} 0.08a-0.08b & =0\\ -0.08a+0.08b & =0 \end{align*}
Hence \(a=b\) then\[ \mathbf{v}_{1}=\frac{1}{\sqrt{2}}\begin{bmatrix} 1\\ 1 \end{bmatrix} =\begin{bmatrix} 0.707\,11\\ 0.707\,11 \end{bmatrix} \] When \(\lambda =\lambda _{2}=19.\,\allowbreak 76\) we obtain\begin{align*} \left ( \begin{bmatrix} 19.\,\allowbreak 68 & -0.08\\ -0.08 & 19.\,\allowbreak 68 \end{bmatrix} -\begin{bmatrix} 19.\,\allowbreak 76 & 0\\ 0 & 19.\,\allowbreak 76 \end{bmatrix} \right ) \begin{bmatrix} a\\ b \end{bmatrix} & =\begin{bmatrix} 0\\ 0 \end{bmatrix} \\\begin{bmatrix} -0.08 & -0.08\\ -0.08 & -0.08 \end{bmatrix}\begin{bmatrix} a\\ b \end{bmatrix} & =\begin{bmatrix} 0\\ 0 \end{bmatrix} \end{align*}
Hence \(a=-b\), then \[ \mathbf{v}_{2}=\frac{1}{\sqrt{2}}\begin{bmatrix} -1\\ 1 \end{bmatrix} =\begin{bmatrix} -0.707\,11\\ 0.707\,11 \end{bmatrix} \] Now that we have obtained the eigenvectors of the de-coupled system, we can plot the mode shapes1 . I will use a diagram similar to that shown in the textbook Engineering Vibration by Inman on page 313)
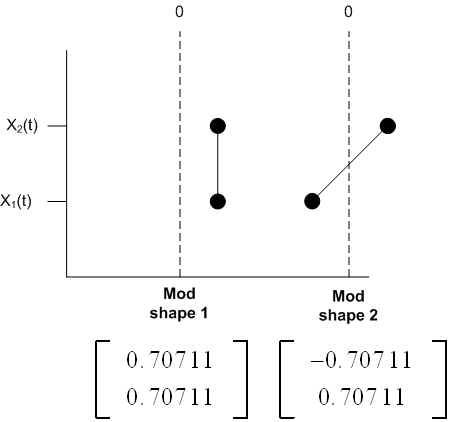
\(\allowbreak \)
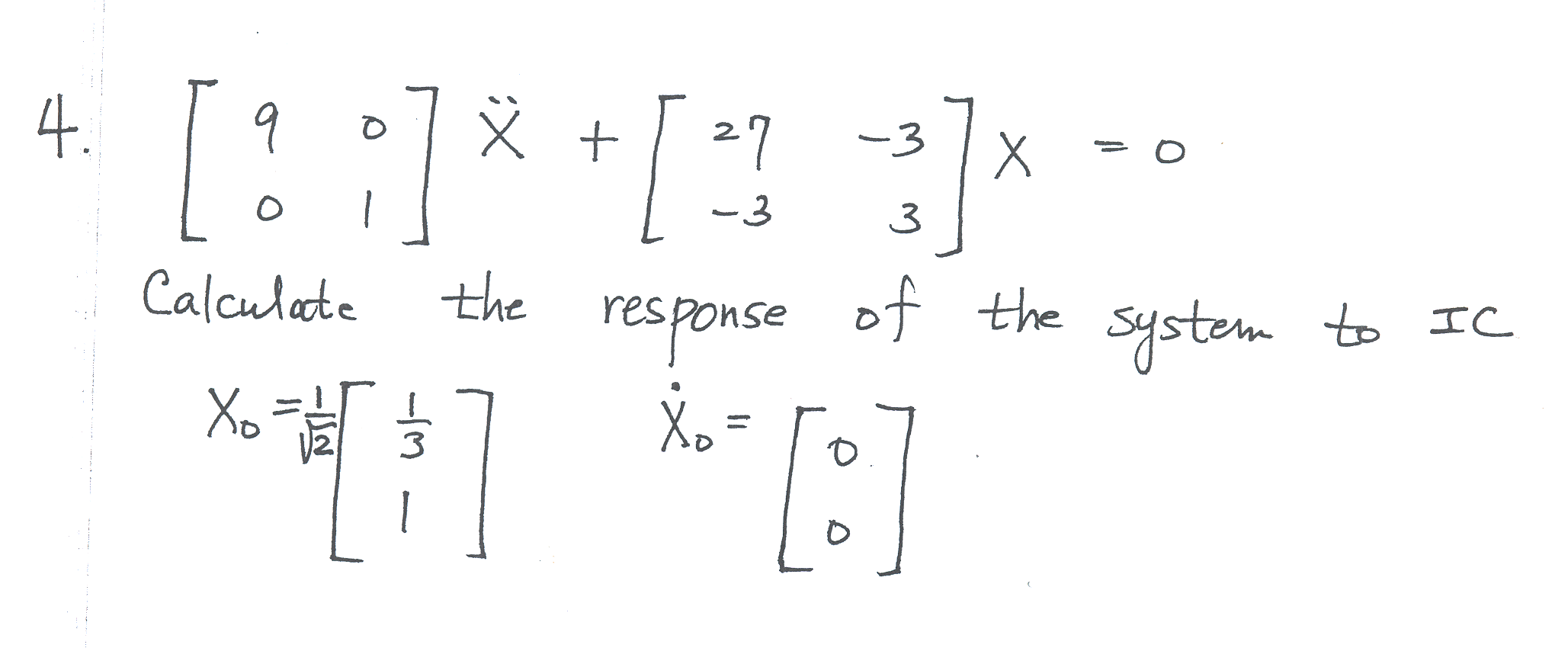
\[ M\mathbf{\ddot{x}+}K\mathbf{x=0}\] Where \(K=\begin{bmatrix} 27 & -3\\ -3 & 3 \end{bmatrix} ,M=\begin{bmatrix} 9 & 0\\ 0 & 1 \end{bmatrix} \) Let \(\mathbf{X}=M^{-\frac{1}{2}}\mathbf{q}\), then \(\mathbf{\ddot{X}}=M^{-\frac{1}{2}}\mathbf{\ddot{q}}\) and the above equation becomes\[ MM^{-\frac{1}{2}}\mathbf{\ddot{q}}+KM^{-\frac{1}{2}}\mathbf{q}=\mathbf{0}\] premultiply by \(M^{-\frac{1}{2}}\) we obtain\begin{align} M^{-\frac{1}{2}}MM^{-\frac{1}{2}}\mathbf{\ddot{q}}+M^{-\frac{1}{2}}KM^{-\frac{1}{2}}\mathbf{q} & =\mathbf{0}\nonumber \\ I\mathbf{\ddot{q}}+\tilde{K}\mathbf{q} & =\mathbf{0} \tag{2} \end{align}
Where \(\tilde{K}=M^{-\frac{1}{2}}KM^{-\frac{1}{2}}\)
Let \(\mathbf{q}=\mathbf{v}e^{i\omega t}\), then \(\mathbf{\ddot{q}=-}\omega ^{2}\mathbf{v}e^{i\omega t}\) and (2) becomes\begin{align*} -\omega ^{2}e^{i\omega t}I\mathbf{v}+\tilde{K}\mathbf{v}e^{i\omega t} & =\mathbf{0}\\ \left ( \tilde{K}-\omega ^{2}I\right ) \mathbf{v} & =\mathbf{0} \end{align*}
Let \(\lambda =\omega ^{2}\) then we have\begin{equation} \left ( \tilde{K}-\lambda I\right ) \mathbf{v}=\mathbf{0} \tag{3} \end{equation} For \(\mathbf{v\neq 0\,}\), we requires that \(\left \vert \tilde{K}-\lambda I\right \vert =0\) But\begin{align*} \tilde{K} & =M^{-\frac{1}{2}}KM^{-\frac{1}{2}}\\ & =\begin{bmatrix} 9^{-\frac{1}{2}} & 0\\ 0 & 1 \end{bmatrix}\begin{bmatrix} 27 & -3\\ -3 & 3 \end{bmatrix}\begin{bmatrix} 9^{-\frac{1}{2}} & 0\\ 0 & 1 \end{bmatrix} \\ & =\begin{bmatrix} 3.0 & -1.0\\ -1.0 & 3.0 \end{bmatrix} \end{align*}
Hence\begin{align*} \left \vert \tilde{K}-\lambda I\right \vert & =0\\ \left \vert \begin{bmatrix} 3.0 & -1.0\\ -1.0 & 3.0 \end{bmatrix} -\lambda \begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix} \right \vert & =0\\ \left \vert \begin{bmatrix} 3-\lambda & -1\\ -1 & 3-\lambda \end{bmatrix} \right \vert & =0\\ \left ( 3-\lambda \right ) ^{2}-1 & =0 \end{align*}
Hence the characteristic equation is\[ \fbox{$\lambda ^{2}-6\lambda +8=0$}\] Hence \[ \fbox{$\lambda _{1,2}=\allowbreak \left \{ 2,\allowbreak 4\right \} $}\] Then the natural frequencies are\[ \omega _{n}=\allowbreak \left \{ \sqrt{2},\allowbreak 2\right \} \] From (3) we then have\begin{align*} \left ( \tilde{K}-\lambda I\right ) \mathbf{v} & =\mathbf{0}\\ \left ( \begin{bmatrix} 3.0 & -1.0\\ -1.0 & 3.0 \end{bmatrix} -\begin{bmatrix} \lambda & 0\\ 0 & \lambda \end{bmatrix} \right ) \mathbf{v} & =\mathbf{0} \end{align*}
When \(\lambda =\lambda _{1}=2\) we obtain\begin{align*} \left ( \begin{bmatrix} 3.0 & -1.0\\ -1.0 & 3.0 \end{bmatrix} -\begin{bmatrix} 2 & 0\\ 0 & 2 \end{bmatrix} \right ) \begin{bmatrix} a\\ b \end{bmatrix} & =\begin{bmatrix} 0\\ 0 \end{bmatrix} \\\begin{bmatrix} 1 & -1\\ -1 & 1 \end{bmatrix}\begin{bmatrix} a\\ b \end{bmatrix} & =\begin{bmatrix} 0\\ 0 \end{bmatrix} \end{align*}
Hence \begin{align*} a-b & =0\\ -a+b & =0 \end{align*}
Then \(a=b\), hence\[ \mathbf{v}_{1}=\frac{1}{\sqrt{2}}\begin{bmatrix} 1\\ 1 \end{bmatrix} =\begin{bmatrix} 0.707\,11\\ 0.707\,11 \end{bmatrix} \] When \(\lambda =\lambda _{2}=4\) we obtain\begin{align*} \left ( \begin{bmatrix} 3.0 & -1.0\\ -1.0 & 3.0 \end{bmatrix} -\begin{bmatrix} 4 & 0\\ 0 & 4 \end{bmatrix} \right ) \begin{bmatrix} a\\ b \end{bmatrix} & =\begin{bmatrix} 0\\ 0 \end{bmatrix} \\\begin{bmatrix} -1 & -1\\ -1 & -1 \end{bmatrix}\begin{bmatrix} a\\ b \end{bmatrix} & =\begin{bmatrix} 0\\ 0 \end{bmatrix} \end{align*}
Hence \(a=-b\), then \[ \mathbf{v}_{2}=\frac{1}{\sqrt{2}}\begin{bmatrix} 1\\ -1 \end{bmatrix} =\begin{bmatrix} 0.707\,11\\ -0.707\,11 \end{bmatrix} \] Then the matrix\begin{align*} \left [ P\right ] & =\begin{bmatrix} \mathbf{v}_{1} & \mathbf{v}_{2}\end{bmatrix} \\ & =\fbox{$\begin{bmatrix} 0.707\,11 & 0.707\,11\\ 0.707\,11 & -0.707\,11 \end{bmatrix} $} \end{align*}
Now let \(\mathbf{q}=P\mathbf{r\,,}\) then equation (2) above becomes\begin{align*} I\mathbf{\ddot{q}}+\tilde{K}\mathbf{q} & =\mathbf{0}\\ IP\mathbf{\ddot{r}}+\tilde{K}P\mathbf{r} & =\mathbf{0} \end{align*}
Premultiply by \(P^{T}\)\begin{align*} P^{T}IP\mathbf{\ddot{r}}+P^{T}\tilde{K}P\mathbf{r} & =\mathbf{0}\\ I\mathbf{\ddot{r}+}P^{T}\tilde{K}P\mathbf{r} & =\mathbf{0} \end{align*}
Let \(\Lambda =P^{T}\tilde{K}P\) then the above becomes\begin{equation} I\mathbf{\ddot{r}+}\Lambda \mathbf{r}=\mathbf{0} \tag{4} \end{equation} Now find \(\Lambda \)
\begin{align*} \Lambda & =P^{T}\tilde{K}P\\ & =\frac{1}{2}\begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix} ^{T}\begin{bmatrix} 3 & -1\\ -1 & 3 \end{bmatrix}\begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix} \\ & =\fbox{$\begin{bmatrix} 2 & 0\\ 0 & 4 \end{bmatrix} $} \end{align*}
Hence (4) becomes\[ I\mathbf{\ddot{r}}+\begin{bmatrix} 2 & 0\\ 0 & 4 \end{bmatrix} \mathbf{r}=\mathbf{0}\] Which can be written as 2 equations\[\begin{bmatrix} \ddot{r}_{1}\\ \ddot{r}_{2}\end{bmatrix} +\begin{bmatrix} 2r_{1}\\ 4r_{2}\end{bmatrix} =\begin{bmatrix} 0\\ 0 \end{bmatrix} \] or\begin{align} \ddot{r}_{1}+2r_{1} & =0\tag{5}\\ \ddot{r}_{2}+4r_{2} & =0 \tag{6} \end{align}
With IC given as \(\mathbf{X}\left ( 0\right ) =\frac{1}{\sqrt{2}}\begin{bmatrix} \frac{1}{3}\\ 1 \end{bmatrix} ,\ \mathbf{\dot{X}}\left ( 0\right ) =\begin{bmatrix} 0\\ 0 \end{bmatrix} \), but
\(\mathbf{X=}M^{-\frac{1}{2}}\mathbf{q}\) and \(\mathbf{q=}P\mathbf{r}\), hence \(\mathbf{X=}M^{-\frac{1}{2}}P\mathbf{r}\), then\begin{align*} \mathbf{r}\left ( 0\right ) & =P^{T}M^{\frac{1}{2}}\mathbf{X}\left ( 0\right ) \\ \mathbf{r}\left ( 0\right ) & =\frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix} ^{T}\begin{bmatrix} 9^{\frac{1}{2}} & 0\\ 0 & 1 \end{bmatrix} \frac{1}{\sqrt{2}}\begin{bmatrix} \frac{1}{3}\\ 1 \end{bmatrix} \\\begin{bmatrix} r_{1}\left ( 0\right ) \\ r_{2}\left ( 0\right ) \end{bmatrix} & =\begin{bmatrix} 1\\ 0 \end{bmatrix} \end{align*}
And since \(\mathbf{\dot{X}}\left ( 0\right ) =\mathbf{0}\), then \(\mathbf{\dot{r}}\left ( 0\right ) =0\), now we have found IC for \(r\left ( t\right ) \) we can solve the ODEs\begin{align*} r_{1}\left ( t\right ) & =A_{1}\cos \sqrt{2}t+B_{1}\sin \sqrt{2}t\\ r_{2}\left ( t\right ) & =A_{2}\cos 2t+B_{2}\sin 2t \end{align*}
\(r_{1}\left ( 0\right ) =1\) hence \(A_{1}=1\), and \(B_{1}=0\), similarly, \(A_{2}=0\), and \(B_{1}=0\), hence\begin{align*} r_{1}\left ( t\right ) & =\cos \sqrt{2}t\\ r_{2}\left ( t\right ) & =0 \end{align*}
But\[ \mathbf{X}\left ( t\right ) \mathbf{=}M^{-\frac{1}{2}}P\mathbf{r}\left ( t\right ) \] Then\begin{align*} \mathbf{X}\left ( t\right ) & \mathbf{=}\begin{bmatrix} 9^{-\frac{1}{2}} & 0\\ 0 & 1 \end{bmatrix} \frac{1}{\sqrt{2}}\begin{bmatrix} 1 & 1\\ 1 & -1 \end{bmatrix} \mathbf{r}\left ( t\right ) \\ & =\frac{1}{\sqrt{2}}\begin{bmatrix} \frac{1}{3} & \frac{1}{3}\\ 1 & -1 \end{bmatrix}\begin{bmatrix} \cos \sqrt{2}t\\ 0 \end{bmatrix} \end{align*}
Hence \[ \fbox{$\begin{bmatrix} x_{1}\left ( t\right ) \\ x_{2}\left ( t\right ) \end{bmatrix} =\begin{bmatrix} \frac{1}{3\sqrt{2}}\left ( \cos \sqrt{2}t\right ) \\ \frac{1}{\sqrt{2}}\left ( \cos \sqrt{2}t\right ) \end{bmatrix} $}\] Here is a plot of the solution
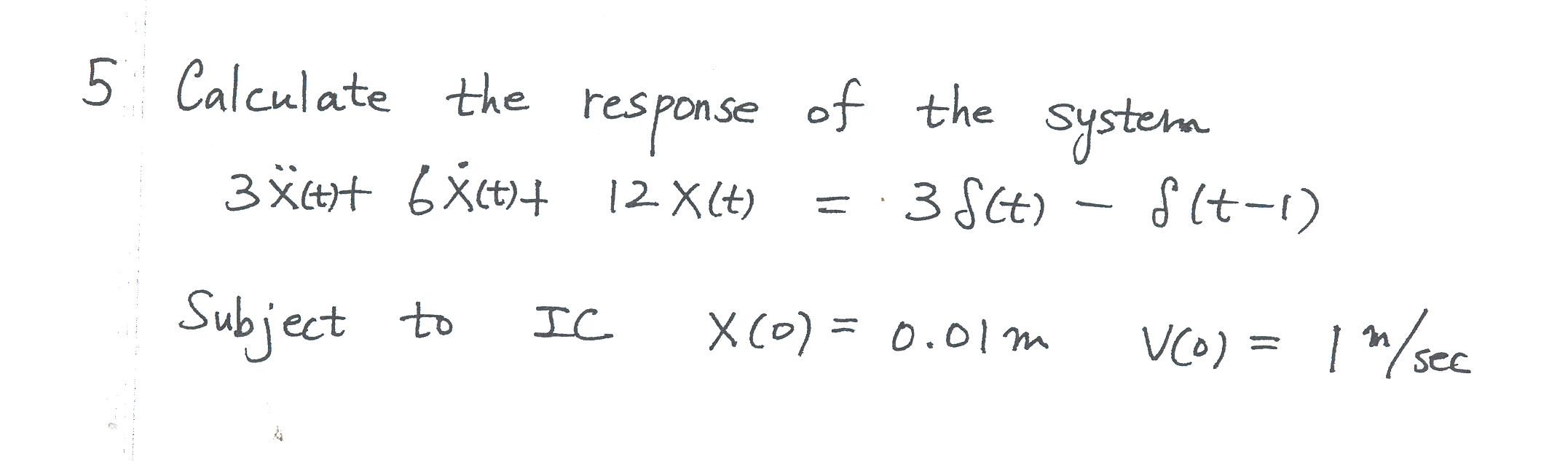
\(m=3,c=6,k=12\), hence \(\omega _{n}=\sqrt{\frac{k}{m}}=\sqrt{\frac{12}{3}}=2\) rad/sec and \(\xi =\frac{c}{c_{cr}}=\frac{c}{2\omega _{n}m}=\frac{6}{2\times 2\times 3}=\frac{1}{2}\), hence the system is underdamped and \(\omega _{d}=\omega _{n}\sqrt{1-\xi ^{2}}=2\sqrt{1-\frac{1}{2}^{2}}=\allowbreak \sqrt{3}\) rad/sec
Let the response to \(3\delta \left ( t\right ) \) be \(x_{p_{1}}\left ( t\right ) \) and let the response to \(\delta \left ( t-1\right ) \) be \(x_{p_{2}}\left ( t\right ) \) hence the response of the system becomes\begin{equation} x\left ( t\right ) =x_{h}\left ( t\right ) +x_{p_{1}}\left ( t\right ) -x_{p_{2}}\left ( t\right ) \tag{1} \end{equation} Where \begin{equation} x_{h}=e^{-\xi \omega _{n}t}\left ( A\cos \omega _{d}t+B\sin \omega _{d}t\right ) \tag{2} \end{equation}
And \begin{equation} x_{p_{1}}\left ( t\right ) =\frac{3}{m\omega _{d}}e^{-\xi \omega _{n}t}\sin \omega _{d}t \tag{3} \end{equation}
and\[ x_{p_{2}}\left ( t\right ) =\frac{1}{m\omega _{d}}e^{-\xi \omega _{n}\left ( t-1\right ) }\sin \omega _{d}\left ( t-1\right ) \Phi \left ( t-1\right ) \] Hence, substitute (2),(3) into (1)\begin{align} x\left ( t\right ) & =e^{-\xi \omega _{n}t}\left ( A\cos \omega _{d}t+B\sin \omega _{d}t\right ) +\frac{3}{m\omega _{d}}e^{-\xi \omega _{n}t}\sin \omega _{d}t\nonumber \\ & +\frac{1}{m\omega _{d}}e^{-\xi \omega _{n}\left ( t-1\right ) }\sin \omega _{d}\left ( t-1\right ) \Phi \left ( t-1\right ) \tag{4} \end{align}
Now using IC to find \(A,B\). Note, we use only \(x\left ( t\right ) =x_{h}\left ( t\right ) +x_{p_{1}}\left ( t\right ) \) for the purpose of finding \(A,B\) from I.C’s since the response to the delayed impulse is not active at \(t=0\). We find \[ x\left ( 0\right ) =\frac{1}{100}=A \] And for the derivative \begin{align*} \dot{x}\left ( t\right ) & =\dot{x}_{h}\left ( t\right ) +\dot{x}_{p_{1}}\left ( t\right ) \\ & =-\xi \omega _{n}e^{-\xi \omega _{n}t}\left ( A\cos \omega _{d}t+B\sin \omega _{d}t\right ) +e^{-\xi \omega _{n}t}\left ( -A\omega _{d}\sin \omega _{d}t+B\omega _{d}\cos \omega _{d}t\right ) \\ & +\frac{3}{m\omega _{d}}e^{-\xi \omega _{n}t}\omega _{d}\cos \omega _{d}t-\frac{3\xi \omega _{n}}{m\omega _{d}}e^{-\xi \omega _{n}t}\sin \omega _{d}t \end{align*}
Hence \begin{align*} \dot{x}\left ( 0\right ) & =1=-\xi \omega _{n}A+B\omega _{d}+\frac{3}{m}\\ 1 & =-\frac{1}{100}+B\omega _{d}+1 \end{align*}
Hence
\[ B=\frac{1}{100\sqrt{3}}\]
Therefore the solution is, by substituting values found for \(A,B\) into the general solution from above equation (4), we obtain\begin{equation} x\left ( t\right ) =\frac{e^{-t}}{100}\left ( \cos \sqrt{3}t+\frac{1}{100\sqrt{3}}\sin \sqrt{3}t\right ) +\frac{1}{\sqrt{3}}e^{-t}\sin \sqrt{3}t-\left ( \frac{1}{3\sqrt{3}}e^{-\left ( t-1\right ) }\sin \sqrt{3}\left ( t-1\right ) \Phi \left ( t-1\right ) \right ) \tag{5} \end{equation} The following is a plot of the solution for up to \(t=6\)
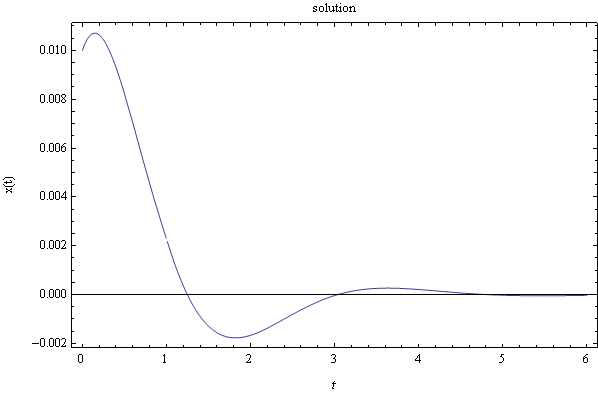
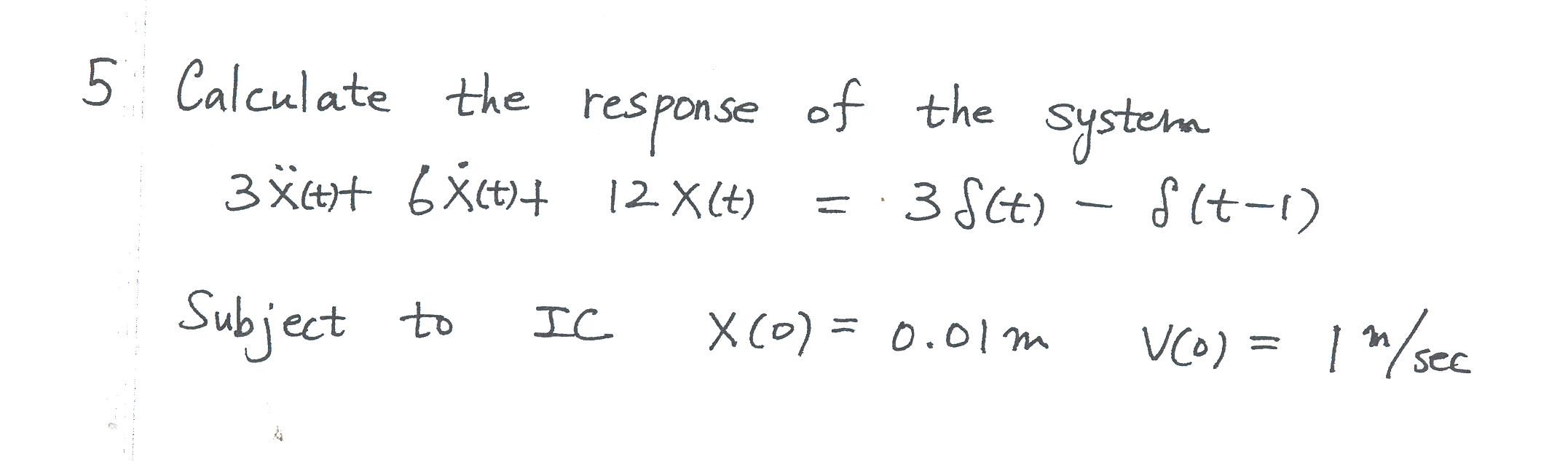
\(m=3,c=6,k=12\), hence \(\omega _{n}=\sqrt{\frac{k}{m}}=\sqrt{\frac{12}{3}}=2\) rad/sec and \(\xi =\frac{c}{c_{cr}}=\frac{c}{2\omega _{n}m}=\frac{6}{2\times 2\times 3}=\frac{1}{2}\), hence the system is underdamped and \(\omega _{d}=\omega _{n}\sqrt{1-\xi ^{2}}=2\sqrt{1-\frac{1}{2}^{2}}=\allowbreak \sqrt{3}\) rad/sec
Let the response to \(3\delta \left ( t\right ) \) be \(x_{p_{1}}\left ( t\right ) \) and let the response to \(\delta \left ( t-1\right ) \) be \(x_{p_{2}}\left ( t\right ) \) hence the response of the system becomes\begin{equation} x\left ( t\right ) =x_{h}\left ( t\right ) +x_{p_{1}}\left ( t\right ) -x_{p_{2}}\left ( t\right ) \tag{1} \end{equation} Where \begin{equation} x_{h}=e^{-\xi \omega _{n}t}\left ( A\cos \omega _{d}t+B\sin \omega _{d}t\right ) \tag{2} \end{equation}
And \begin{equation} x_{p_{1}}\left ( t\right ) =\frac{3}{m\omega _{d}}e^{-\xi \omega _{n}t}\sin \omega _{d}t \tag{3} \end{equation}
and\[ x_{p_{2}}\left ( t\right ) =\frac{1}{m\omega _{d}}e^{-\xi \omega _{n}\left ( t-1\right ) }\sin \omega _{d}\left ( t-1\right ) \Phi \left ( t-1\right ) \] To find \(A,B\) use only \(x_{h}\left ( t\right ) .\)At \(t=0\). We find \[ x\left ( 0\right ) =\frac{1}{100}=A \] And for the derivative \begin{align*} \dot{x}\left ( t\right ) & =\dot{x}_{h}\left ( t\right ) \\ & =-\xi \omega _{n}e^{-\xi \omega _{n}t}\left ( A\cos \omega _{d}t+B\sin \omega _{d}t\right ) +e^{-\xi \omega _{n}t}\left ( -A\omega _{d}\sin \omega _{d}t+B\omega _{d}\cos \omega _{d}t\right ) \end{align*}
Hence \begin{align*} \dot{x}\left ( 0\right ) & =1=-\xi \omega _{n}A+B\omega _{d}\\ 1 & =-\frac{1}{100}+B\omega _{d} \end{align*}
Hence
\begin{align*} B & =\frac{1+\frac{1}{100}}{\sqrt{3}}\\ & =\frac{101}{100\sqrt{3}} \end{align*}
Therefore the solution is, by substituting values found for \(A,B\) into the general solution from above equation (4), we obtain\begin{equation} x\left ( t\right ) =\frac{e^{-t}}{100}\left ( \cos \sqrt{3}t+\frac{101}{100\sqrt{3}}\sin \sqrt{3}t\right ) +\frac{1}{\sqrt{3}}e^{-t}\sin \sqrt{3}t-\left ( \frac{1}{3\sqrt{3}}e^{-\left ( t-1\right ) }\sin \sqrt{3}\left ( t-1\right ) \Phi \left ( t-1\right ) \right ) \tag{5} \end{equation} The following is a plot of the solution for up to \(t=6\)

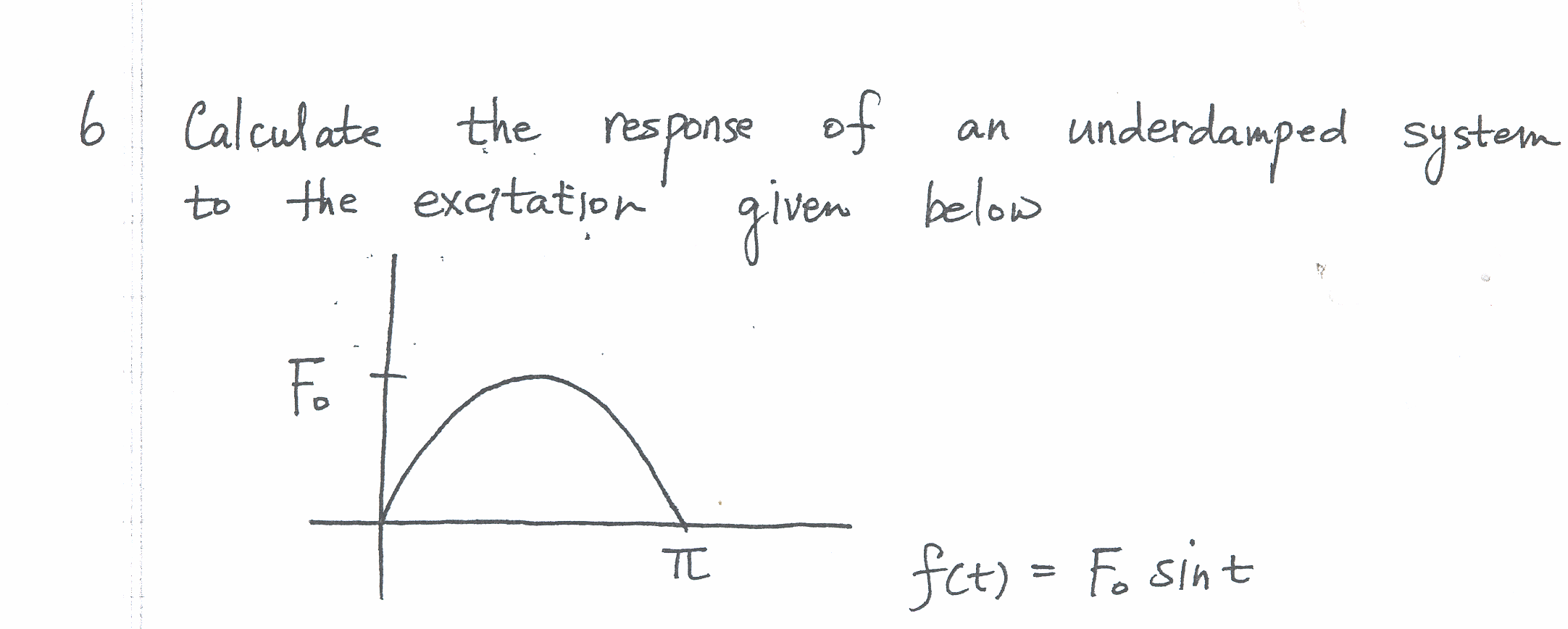
Using \(\sin A\sin B=\frac{1}{2}\left [ \cos \left ( A-B\right ) -\cos \left ( A+B\right ) \right ] \,\ \) then \[ \sin \left ( \tau \right ) \sin \left ( \omega _{d}\left ( t-\tau \right ) \right ) =\frac{1}{2}\left [ \cos \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) -\cos \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) \right ] \] Then the integral becomes\[ x_{p}\left ( t\right ) =\frac{F_{0}e^{-\xi \omega _{n}t}}{2m\omega _{d}}\left ({\displaystyle \int \limits _{0}^{t}} e^{\xi \omega _{n}\tau }\cos \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) d\tau -{\displaystyle \int \limits _{0}^{t}} e^{\xi \omega _{n}\tau }\cos \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) d\tau \right ) \] Consider the first integral \(I_{1}\) where\[ I_{1}={\displaystyle \int \limits _{0}^{t}} e^{\xi \omega _{n}\tau }\cos \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) d\tau \] Integrate by parts, where \(\int udv=uv-\int vdu\), Let \(dv=e^{\xi \omega _{n}\tau }\rightarrow v=\frac{e^{\xi \omega _{n}\tau }}{\xi \omega _{n}}\) and let \(u=\cos \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) \rightarrow du=-\left ( 1+\omega _{d}\right ) \sin \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) \), hence\begin{align} I_{1} & =\left [ \cos \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) \frac{e^{\xi \omega _{n}\tau }}{\xi \omega _{n}}\right ] _{0}^{t}-{\displaystyle \int \limits _{0}^{t}} \frac{e^{\xi \omega _{n}\tau }}{\xi \omega _{n}}\left [ -\left ( 1+\omega _{d}\right ) \sin \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) \right ] d\tau \nonumber \\ & =\left [ \cos \left ( t-\omega _{d}\left ( t-t\right ) \right ) \frac{e^{\xi \omega _{n}t}}{\xi \omega _{n}}-\cos \left ( 0-\omega _{d}\left ( t-0\right ) \right ) \frac{1}{\xi \omega _{n}}\right ] +\frac{\left ( 1+\omega _{d}\right ) }{\xi \omega _{n}}{\displaystyle \int \limits _{0}^{t}} e^{\xi \omega _{n}\tau }\sin \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) d\tau \nonumber \\ & =\frac{1}{\xi \omega _{n}}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\frac{\left ( 1+\omega _{d}\right ) }{\xi \omega _{n}}{\displaystyle \int \limits _{0}^{t}} e^{\xi \omega _{n}\tau }\sin \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) d\tau \tag{1} \end{align}
Integrate by parts again the last integral above, where \(\int udv=uv-\int vdu\), Let \(dv=e^{\xi \omega _{n}\tau }\rightarrow v=\frac{e^{\xi \omega _{n}\tau }}{\xi \omega _{n}}\) and let \(u=\sin \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) \rightarrow du=\left ( 1+\omega _{d}\right ) \cos \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) \), hence\begin{align}{\displaystyle \int \limits _{0}^{t}} e^{\xi \omega _{n}\tau }\sin \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) d\tau & =\left [ \sin \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) \frac{e^{\xi \omega _{n}\tau }}{\xi \omega _{n}}\right ] _{0}^{t}-\int _{0}^{t}\frac{e^{\xi \omega _{n}\tau }}{\xi \omega _{n}}\left ( 1+\omega _{d}\right ) \cos \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) d\tau \nonumber \\ & =\frac{1}{\xi \omega _{n}}\left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] -\frac{\left ( 1+\omega _{d}\right ) }{\xi \omega _{n}}\int _{0}^{t}e^{\xi \omega _{n}\tau }\cos \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) d\tau \tag{2} \end{align}
Substitute (2) into (1) we obtain\begin{align*} I_{1} & =\frac{1}{\xi \omega _{n}}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\\ & \frac{\left ( 1+\omega _{d}\right ) }{\xi \omega _{n}}\left ( \frac{1}{\xi \omega _{n}}\left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] -\frac{\left ( 1+\omega _{d}\right ) }{\xi \omega _{n}}\int _{0}^{t}e^{\xi \omega _{n}\tau }\cos \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) d\tau \right ) \\ & \\ & =\frac{1}{\xi \omega _{n}}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\frac{\left ( 1+\omega _{d}\right ) }{\left ( \xi \omega _{n}\right ) ^{2}}\left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] -\frac{\left ( 1+\omega _{d}\right ) ^{2}}{\left ( \xi \omega _{n}\right ) ^{2}}\int _{0}^{t}e^{\xi \omega _{n}\tau }\cos \left ( \tau -\omega _{d}\left ( t-\tau \right ) \right ) d\tau \\ & \\ & =\frac{1}{\xi \omega _{n}}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\frac{\left ( 1+\omega _{d}\right ) }{\left ( \xi \omega _{n}\right ) ^{2}}\left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] -\frac{\left ( 1+\omega _{d}\right ) ^{2}}{\left ( \xi \omega _{n}\right ) ^{2}}I_{1} \end{align*}
Hence\begin{align*} I_{1}+\frac{\left ( 1+\omega _{d}\right ) ^{2}}{\left ( \xi \omega _{n}\right ) ^{2}}I_{1} & =\frac{1}{\xi \omega _{n}}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\frac{\left ( 1+\omega _{d}\right ) }{\left ( \xi \omega _{n}\right ) ^{2}}\left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] \\ I_{1}\left ( \frac{\left ( \xi \omega _{n}\right ) ^{2}+\left ( 1+\omega _{d}\right ) ^{2}}{\left ( \xi \omega _{n}\right ) ^{2}}\right ) & =\frac{1}{\xi \omega _{n}}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\frac{\left ( 1+\omega _{d}\right ) }{\left ( \xi \omega _{n}\right ) ^{2}}\left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] \\ I_{1} & =\left ( \frac{\left ( \xi \omega _{n}\right ) ^{2}}{\left ( \xi \omega _{n}\right ) ^{2}+\left ( 1+\omega _{d}\right ) ^{2}}\right ) \left ( \frac{1}{\xi \omega _{n}}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\frac{\left ( 1+\omega _{d}\right ) }{\left ( \xi \omega _{n}\right ) ^{2}}\left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] \right ) \\ & =\frac{\xi \omega _{n}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\left ( 1+\omega _{d}\right ) \left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] }{\left ( \xi \omega _{n}\right ) ^{2}+\left ( 1+\omega _{d}\right ) ^{2}} \end{align*}
Now consider the second integral \(I_{2}\) where\[ I_{2}={\displaystyle \int \limits _{0}^{t}} e^{\xi \omega _{n}\tau }\cos \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) d\tau \] Integrate by parts, where \(\int udv=uv-\int vdu\), Let \(dv=e^{\xi \omega _{n}\tau }\rightarrow v=\frac{e^{\xi \omega _{n}\tau }}{\xi \omega _{n}}\) and let \(u=\cos \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) \rightarrow du=-\left ( 1-\omega _{d}\right ) \sin \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) \), hence\begin{align} I_{2} & =\left [ \cos \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) \frac{e^{\xi \omega _{n}\tau }}{\xi \omega _{n}}\right ] _{0}^{t}-{\displaystyle \int \limits _{0}^{t}} \frac{e^{\xi \omega _{n}\tau }}{\xi \omega _{n}}\left [ -\left ( 1-\omega _{d}\right ) \sin \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) \right ] d\tau \nonumber \\ & =\left [ \cos \left ( t+\omega _{d}\left ( t-t\right ) \right ) \frac{e^{\xi \omega _{n}t}}{\xi \omega _{n}}-\cos \left ( 0+\omega _{d}\left ( t-0\right ) \right ) \frac{1}{\xi \omega _{n}}\right ] +\frac{\left ( 1-\omega _{d}\right ) }{\xi \omega _{n}}{\displaystyle \int \limits _{0}^{t}} e^{\xi \omega _{n}\tau }\sin \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) d\tau \nonumber \\ & =\frac{1}{\xi \omega _{n}}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\frac{\left ( 1-\omega _{d}\right ) }{\xi \omega _{n}}{\displaystyle \int \limits _{0}^{t}} e^{\xi \omega _{n}\tau }\sin \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) d\tau \tag{3} \end{align}
Integrate by parts again the last integral above, where \(\int udv=uv-\int vdu\), Let \(dv=e^{\xi \omega _{n}\tau }\rightarrow v=\frac{e^{\xi \omega _{n}\tau }}{\xi \omega _{n}}\) and let \(u=\sin \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) \rightarrow du=\left ( 1-\omega _{d}\right ) \cos \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) \), hence\begin{align}{\displaystyle \int \limits _{0}^{t}} e^{\xi \omega _{n}\tau }\sin \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) d\tau & =\left [ \sin \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) \frac{e^{\xi \omega _{n}\tau }}{\xi \omega _{n}}\right ] _{0}^{t}-\int _{0}^{t}\frac{e^{\xi \omega _{n}\tau }}{\xi \omega _{n}}\left ( 1-\omega _{d}\right ) \cos \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) d\tau \nonumber \\ & =\frac{1}{\xi \omega _{n}}\left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}-\sin \left ( \omega _{d}t\right ) \right ] -\frac{\left ( 1-\omega _{d}\right ) }{\xi \omega _{n}}\int _{0}^{t}e^{\xi \omega _{n}\tau }\cos \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) d\tau \tag{4} \end{align}
Substitute (4) into (3) we obtain\begin{align*} I_{2} & =\frac{1}{\xi \omega _{n}}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\\ & \frac{\left ( 1-\omega _{d}\right ) }{\xi \omega _{n}}\left ( \frac{1}{\xi \omega _{n}}\left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}-\sin \left ( \omega _{d}t\right ) \right ] -\frac{\left ( 1-\omega _{d}\right ) }{\xi \omega _{n}}\int _{0}^{t}e^{\xi \omega _{n}\tau }\cos \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) d\tau \right ) \\ & \\ & =\frac{1}{\xi \omega _{n}}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\frac{\left ( 1-\omega _{d}\right ) }{\left ( \xi \omega _{n}\right ) ^{2}}\left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}-\sin \left ( \omega _{d}t\right ) \right ] -\frac{\left ( 1-\omega _{d}\right ) ^{2}}{\left ( \xi \omega _{n}\right ) ^{2}}\int _{0}^{t}e^{\xi \omega _{n}\tau }\cos \left ( \tau +\omega _{d}\left ( t-\tau \right ) \right ) d\tau \\ & \\ & =\frac{1}{\xi \omega _{n}}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\frac{\left ( 1-\omega _{d}\right ) }{\left ( \xi \omega _{n}\right ) ^{2}}\left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] -\frac{\left ( 1-\omega _{d}\right ) ^{2}}{\left ( \xi \omega _{n}\right ) ^{2}}I_{2} \end{align*}
Hence\begin{align*} I_{2}+\frac{\left ( 1-\omega _{d}\right ) ^{2}}{\left ( \xi \omega _{n}\right ) ^{2}}I_{2} & =\frac{1}{\xi \omega _{n}}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\frac{\left ( 1-\omega _{d}\right ) }{\left ( \xi \omega _{n}\right ) ^{2}}\left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] \\ I_{2}\left ( \frac{\left ( \xi \omega _{n}\right ) ^{2}+\left ( 1-\omega _{d}\right ) ^{2}}{\left ( \xi \omega _{n}\right ) ^{2}}\right ) & =\frac{1}{\xi \omega _{n}}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\frac{\left ( 1-\omega _{d}\right ) }{\left ( \xi \omega _{n}\right ) ^{2}}\left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] \\ I_{2} & =\left ( \frac{\left ( \xi \omega _{n}\right ) ^{2}}{\left ( \xi \omega _{n}\right ) ^{2}+\left ( 1-\omega _{d}\right ) ^{2}}\right ) \left ( \frac{1}{\xi \omega _{n}}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\frac{\left ( 1-\omega _{d}\right ) }{\left ( \xi \omega _{n}\right ) ^{2}}\left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] \right ) \\ & =\frac{\xi \omega _{n}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\left ( 1-\omega _{d}\right ) \left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] }{\left ( \xi \omega _{n}\right ) ^{2}+\left ( 1-\omega _{d}\right ) ^{2}} \end{align*}
Using the above expressions for \(I_{1},I_{2}\), we find (and multiplying the solution by \(\left ( \Phi \left ( t\right ) -\Phi \left ( t-\pi \right ) \right ) \) since the force is only active from \(t=0\) to \(t=\pi \), we obtain\begin{align} x_{p}\left ( t\right ) & =\frac{F_{0}e^{-\xi \omega _{n}t}}{2m\omega _{d}}\left ( I_{1}-I_{2}\right ) \left ( \Phi \left ( t\right ) -\Phi \left ( t-\pi \right ) \right ) \nonumber \\ & \nonumber \\ & =\left ( \Phi \left ( t\right ) -\Phi \left ( t-\pi \right ) \right ) \ast \nonumber \\ & \frac{F_{0}e^{-\xi \omega _{n}t}}{2m\omega _{d}}\frac{\xi \omega _{n}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\left ( 1+\omega _{d}\right ) \left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] }{\left ( \xi \omega _{n}\right ) ^{2}+\left ( 1+\omega _{d}\right ) ^{2}}\nonumber \\ & -\frac{F_{0}e^{-\xi \omega _{n}t}}{2m\omega _{d}}\frac{\xi \omega _{n}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\left ( 1-\omega _{d}\right ) \left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] }{\left ( \xi \omega _{n}\right ) ^{2}+\left ( 1-\omega _{d}\right ) ^{2}} \tag{5} \end{align}
Hence \(x_{p}\left ( t\right ) =\left ( \Phi \left ( t\right ) -\Phi \left ( t-\pi \right ) \right ) \)
\(\left [ \frac{F_{0}e^{-\xi \omega _{n}t}}{2m\omega _{d}}\left ( \frac{\xi \omega _{n}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\left ( 1+\omega _{d}\right ) \left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] }{\left ( \xi \omega _{n}\right ) ^{2}+\left ( 1+\omega _{d}\right ) ^{2}}-\frac{\xi \omega _{n}\left [ \cos \left ( t\right ) e^{\xi \omega _{n}t}-\cos \left ( \omega _{d}t\right ) \right ] +\left ( 1-\omega _{d}\right ) \left [ \sin \left ( t\right ) e^{\xi \omega _{n}t}+\sin \left ( \omega _{d}t\right ) \right ] }{\left ( \xi \omega _{n}\right ) ^{2}+\left ( 1-\omega _{d}\right ) ^{2}}\right ) \right ] \)
And \[ x_{h}\left ( t\right ) =e^{-\xi \omega _{n}t}\left ( A\cos \omega _{d}t+B\sin \omega _{d}t\right ) \] Hence the overall solution is\[ x\left ( t\right ) =e^{-\xi \omega _{n}t}\left ( A\cos \omega _{d}t+B\sin \omega _{d}t\right ) +x_{p}\left ( t\right ) \] The above solution is a bit long due to integration by parts. I will not solve the same problem using Laplace transformation method. The differential equation is\[ \ddot{x}\left ( t\right ) +2\xi \omega _{n}\dot{x}\left ( t\right ) +\omega _{n}^{2}x\left ( t\right ) =f\left ( t\right ) \] Take Laplace transform, we obtain (assuming \(x\left ( 0\right ) =x_{0}\) and \(\dot{x}\left ( 0\right ) =v_{0}\))\begin{align} \left ( s^{2}X-sx\left ( 0\right ) -\dot{x}\left ( 0\right ) \right ) +2\xi \omega _{n}\left ( sX-x\left ( 0\right ) \right ) +\omega _{n}^{2}X & =F\left ( s\right ) \nonumber \\ \left ( s^{2}X-sx_{0}-v_{0}\right ) +2\xi \omega _{n}\left ( sX-x_{0}\right ) +\omega _{n}^{2}X & =F\left ( s\right ) \tag{7} \end{align}
Now we find Laplace transform of \(f\left ( t\right ) \)\begin{align*} F\left ( s\right ) & ={\displaystyle \int \limits _{0}^{\infty }} e^{-st}f\left ( t\right ) dt\\ & ={\displaystyle \int \limits _{0}^{\pi }} e^{-st}F_{0}\sin t\ dt\\ & =F_{0}\left [{\displaystyle \int \limits _{0}^{\pi }} e^{-st}\sin t\ dt\right ] \end{align*}
Integration by parts gives\begin{equation} F\left ( s\right ) =F_{0}\left [ \frac{1+e^{-\pi s}}{1+s^{2}}\right ] \tag{8} \end{equation} Substitute (8) into (7) we obtain\begin{align*} \left ( s^{2}X-sx_{0}-v_{0}\right ) +2\xi \omega _{n}\left ( sX-x_{0}\right ) +\omega _{n}^{2}X & =F_{0}\left [ \frac{1+e^{-\pi s}}{1+s^{2}}\right ] \\ X\left ( s^{2}+2\xi \omega _{n}s+\omega _{n}^{2}\right ) -sx_{0}-v_{0}-2\xi \omega _{n}x_{0} & =\frac{F_{0}\left ( 1+e^{-\pi s}\right ) }{1+s^{2}}\\ X\left ( s^{2}+2\xi \omega _{n}s+\omega _{n}^{2}\right ) & =\frac{F_{0}\left ( 1+e^{-\pi s}\right ) }{1+s^{2}}+sx_{0}+v_{0}+2\xi \omega _{n}x_{0}\\ & =\frac{F_{0}\left ( 1+e^{-\pi s}\right ) +\left ( 1+s^{2}\right ) sx_{0}+v_{0}\left ( 1+s^{2}\right ) +2\xi \omega _{n}x_{0}\left ( 1+s^{2}\right ) }{1+s^{2}} \end{align*}
Hence\begin{align*} X & =\frac{F_{0}\left ( 1+e^{-\pi s}\right ) +\left ( 1+s^{2}\right ) sx_{0}+v_{0}\left ( 1+s^{2}\right ) +2\xi \omega _{n}x_{0}\left ( 1+s^{2}\right ) }{\left ( 1+s^{2}\right ) \left ( s^{2}+2\xi \omega _{n}s+\omega _{n}^{2}\right ) }\\ & =\frac{F_{0}+v_{0}+\frac{F_{0}}{e^{\pi s}}+sx_{0}+s^{2}v_{0}+s^{3}x_{0}+2\xi \omega _{n}\allowbreak x_{0}+2s^{2}\xi \omega _{n}x_{0}}{\left ( 1+s^{2}\right ) \left ( s^{2}+2\xi \omega _{n}s+\omega _{n}^{2}\right ) } \end{align*}
Now we can use inverse Laplace transform on the above. It is easier to do partial fraction decomposition and use tables. I used CAS to do this and this is the result. I plot the solution \(x\left ( t\right ) \). I used the following values to be able to obtain a plot \(\xi =0.5,\omega _{n}=2,F_{0}=10,x_{0}=1,v_{0}=0\)
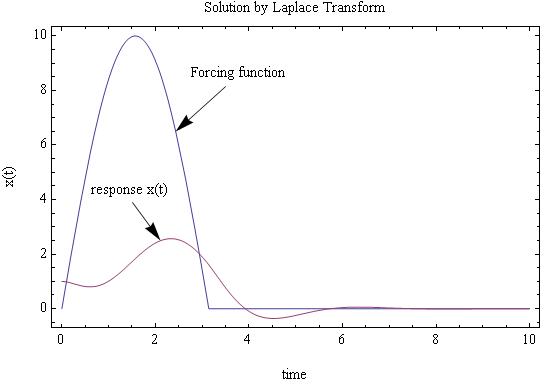
Problem
Solve \(\ddot{x}+2\dot{x}+4x=\delta \left ( t\right ) -\delta \left ( t-4\right ) \) with the IC’s \(x\left ( 0\right ) =1mm,\dot{x}\left ( 0\right ) =-1mm\)
Answer
\(m=1,c=2,k=4\), hence \(\omega _{n}=\sqrt{\frac{k}{m}}=\sqrt{4}=2\) rad/sec and \(\xi =\frac{c}{c_{cr}}=\frac{c}{2\omega _{n}m}=\frac{2}{2\times 2\times 1}=\frac{1}{2}\), hence the system is underdamped and \(\omega _{d}=\omega _{n}\sqrt{1-\xi ^{2}}=2\sqrt{1-\frac{1}{2}^{2}}=\allowbreak \sqrt{3}\) rad/sec
Let the response to \(\delta \left ( t\right ) \) be \(x_{1}\left ( t\right ) \) and let the response to \(\delta \left ( t-4\right ) \) be \(x_{2}\left ( t\right ) \) hence the response of the system becomes\begin{equation} x\left ( t\right ) =x_{h}\left ( t\right ) +x_{1}\left ( t\right ) -x_{2}\left ( t\right ) \tag{1} \end{equation} Where \begin{equation} x_{h}=e^{-\xi \omega _{n}t}\left ( A\cos \omega _{d}t+B\sin \omega _{d}t\right ) \tag{1} \end{equation} And \begin{equation} x_{1}\left ( t\right ) =\frac{1}{m\omega _{d}}e^{-\xi \omega _{n}t}\sin \omega _{d}t\tag{3} \end{equation} and\[ x_{2}\left ( t\right ) =\frac{1}{m\omega _{d}}e^{-\xi \omega _{n}\left ( t-4\right ) }\sin \omega _{d}\left ( t-4\right ) \Phi \left ( t-4\right ) \] Hence, substitute (2),(3) ,(4) into (1)\begin{equation} x\left ( t\right ) =e^{-\xi \omega _{n}t}\left ( A\cos \omega _{d}t+B\sin \omega _{d}t\right ) +\frac{1}{m\omega _{d}}e^{-\xi \omega _{n}t}\sin \omega _{d}t-\frac{1}{m\omega _{d}}e^{-\xi \omega _{n}\left ( t-4\right ) }\sin \left ( \omega _{d}\left ( t-4\right ) \right ) \Phi \left ( t-4\right ) \tag{4} \end{equation} Now using IC to find \(A,B\)\[ x\left ( 0\right ) =1=A \] and\begin{align*} \dot{x}\left ( t\right ) & =-\xi \omega _{n}e^{-\xi \omega _{n}t}\left ( A\cos \omega _{d}t+B\sin \omega _{d}t\right ) +e^{-\xi \omega _{n}t}\left ( -A\omega _{d}\sin \omega _{d}t+B\omega _{d}\cos \omega _{d}t\right ) +\\ & \frac{1}{m\omega _{d}}\left ( -\xi \omega _{n}e^{-\xi \omega _{n}t}\sin \omega _{d}t+\omega _{d}e^{-\xi \omega _{n}t}\cos \omega _{d}t\right ) -\\ & \frac{e^{-\xi \omega _{n}\left ( t-4\right ) }}{m\omega _{d}}\left ( \omega _{d}\cos \left ( \omega _{d}\left ( t-4\right ) \right ) \Phi \left ( t-4\right ) +\delta \left ( t-4\right ) \sin \left ( \omega _{d}\left ( t-4\right ) \right ) -\xi \omega _{n}\omega _{d}\sin \left ( \omega _{d}\left ( t-4\right ) \right ) \Phi \left ( t-4\right ) \right ) \end{align*}
At \(t=0,\dot{x}\left ( 0\right ) =-1,\) Hence the above becomes (terms with \(\delta \left ( t-4\right ) \) and \(\Phi \left ( t-4\right ) \) vanish at \(t=0\) by definition)\begin{align*} -1 & =-\xi \omega _{n}A+B\omega _{d}+\frac{1}{m}\\ B & =\frac{-1}{\sqrt{3}} \end{align*}
Hence (1) becomes\[ x\left ( t\right ) =e^{-\xi \omega _{n}t}\left ( \cos \omega _{d}t-\frac{1}{\sqrt{3}}\sin \omega _{d}t\right ) +\frac{1}{m\omega _{d}}e^{-\xi \omega _{n}t}\sin \omega _{d}t-\frac{1}{m\omega _{d}}e^{-\xi \omega _{n}\left ( t-4\right ) }\sin \left ( \omega _{d}\left ( t-4\right ) \right ) \Phi \left ( t-4\right ) \] If we substitute the numerical values for the problem parameters, the above becomes\begin{align*} x\left ( t\right ) & =e^{-t}\left ( \cos \sqrt{3}t-\frac{1}{\sqrt{3}}\sin \sqrt{3}t\right ) +\frac{e^{-t}}{\sqrt{3}}\sin \sqrt{3}t-\frac{1}{\sqrt{3}}e^{-\left ( t-4\right ) }\sin \left ( \sqrt{3}\left ( t-4\right ) \right ) \Phi \left ( t-4\right ) \\ & =\fbox{$e^{-t}\cos \sqrt{3}t-\frac{1}{\sqrt{3}}e^{-\left ( t-4\right ) }\sin \left ( \sqrt{3}\left ( t-4\right ) \right ) \Phi \left ( t-4\right ) $} \end{align*}
Compare the above with the solution given in class, which is\[ x\left ( t\right ) =\fbox{$e^{-t}\left ( \cos \sqrt{3}t+\frac{1}{\sqrt{3}}\sin \sqrt{3}t\right ) -\frac{1}{\sqrt{3}}e^{-\left ( t-4\right ) }\sin \left ( \sqrt{3}\left ( t-4\right ) \right ) \Phi \left ( t-4\right ) $}\]
Problem
Solve \(\ddot{x}+2\dot{x}+4x=\delta \left ( t\right ) -\delta \left ( t-4\right ) \) with the IC’s \(x\left ( 0\right ) =1mm,\dot{x}\left ( 0\right ) =-1mm\)
Answer
\(m=1,c=2,k=4\), hence \(\omega _{n}=\sqrt{\frac{k}{m}}=\sqrt{4}=2\) rad/sec and \(\xi =\frac{c}{c_{cr}}=\frac{c}{2\omega _{n}m}=\frac{2}{2\times 2\times 1}=\frac{1}{2}\), hence the system is underdamped and \(\omega _{d}=\omega _{n}\sqrt{1-\xi ^{2}}=2\sqrt{1-\frac{1}{2}^{2}}=\allowbreak \sqrt{3}\) rad/sec
Let the response to \(\delta \left ( t\right ) \) be \(x_{p_{1}}\left ( t\right ) \) and let the response to \(\delta \left ( t-4\right ) \) be \(x_{p_{2}}\left ( t\right ) \) hence the response of the system becomes\begin{equation} x\left ( t\right ) =x_{h}\left ( t\right ) +x_{p_{1}}\left ( t\right ) -x_{p_{2}}\left ( t\right ) \tag{1} \end{equation} Where \begin{equation} x_{h}=e^{-\xi \omega _{n}t}\left ( A\cos \omega _{d}t+B\sin \omega _{d}t\right ) \tag{1} \end{equation} And \begin{equation} x_{p_{1}}\left ( t\right ) =\frac{1}{m\omega _{d}}e^{-\xi \omega _{n}t}\sin \omega _{d}t\tag{3} \end{equation} and\[ x_{p_{2}}\left ( t\right ) =\frac{1}{m\omega _{d}}e^{-\xi \omega _{n}\left ( t-4\right ) }\sin \omega _{d}\left ( t-4\right ) \Phi \left ( t-4\right ) \] Hence, substitute (2),(3) ,(4) into (1)\begin{equation} x\left ( t\right ) =e^{-\xi \omega _{n}t}\left ( A\cos \omega _{d}t+B\sin \omega _{d}t\right ) +\frac{1}{m\omega _{d}}e^{-\xi \omega _{n}t}\sin \omega _{d}t-\frac{1}{m\omega _{d}}e^{-\xi \omega _{n}\left ( t-4\right ) }\sin \left ( \omega _{d}\left ( t-4\right ) \right ) \Phi \left ( t-4\right ) \tag{4} \end{equation} Now using IC to find \(A,B\)\[ x\left ( 0\right ) =1 \]
Hence \[ \fbox{$A=1$}\]
Now take the derivative of the above and evaluate at zero to find \(B\). In doing so, we need to consider only the \(x_{h}\). The reason is that the particular solution \(x_{p_{2}}\left ( t\right ) \) of the delayed pulse (the second pulse) will have no effect at \(t=0\,\) and the first pulse particular solution \(x_{p_{1}}\left ( t\right ) \) will also have no contribution, since its response is assume to occur at \(0^{+}\), i.e. an infitismal time after \(t=0\). Therefore, since we intend to evaluate \(\dot{x}\left ( t\right ) \) at \(t=0\), we only need to take \(x_{h}\) derivative at this point
\[ \dot{x}\left ( t\right ) =-\xi \omega _{n}e^{-\xi \omega _{n}t}\left ( A\cos \omega _{d}t+B\sin \omega _{d}t\right ) +e^{-\xi \omega _{n}t}\left ( -A\omega _{d}\sin \omega _{d}t+B\omega _{d}\cos \omega _{d}t\right ) \] At \(t=0,\dot{x}\left ( 0\right ) =-1,\) Hence the above becomes\begin{align*} -1 & =-\xi \omega _{n}A+B\omega _{d}\\ -1 & =-1+B\sqrt{3}\\ & \fbox{$B=0$} \end{align*}
Hence (1) becomes\[ x\left ( t\right ) =e^{-\xi \omega _{n}t}\cos \omega _{d}t+\frac{1}{m\omega _{d}}e^{-\xi \omega _{n}t}\sin \omega _{d}t-\frac{1}{m\omega _{d}}e^{-\xi \omega _{n}\left ( t-4\right ) }\sin \left ( \omega _{d}\left ( t-4\right ) \right ) \Phi \left ( t-4\right ) \] If we substitute the numerical values for the problem parameters, the above becomes\begin{align*} x\left ( t\right ) & =e^{-t}\cos \sqrt{3}t+\frac{e^{-t}}{\sqrt{3}}\sin \sqrt{3}t-\frac{1}{\sqrt{3}}e^{-\left ( t-4\right ) }\sin \left ( \sqrt{3}\left ( t-4\right ) \right ) \Phi \left ( t-4\right ) \\ & =\fbox{$e^{-t}\left ( \cos \sqrt{3}t+\frac{1}{\sqrt{3}}\sin \sqrt{3}t\right ) -\frac{1}{\sqrt{3}}e^{-\left ( t-4\right ) }\sin \left ( \sqrt{3}\left ( t-4\right ) \right ) \Phi \left ( t-4\right ) $} \end{align*}
Which now matches the solution given in class