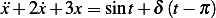 with IC
with IC 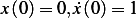 and plot the
solution.
and plot the
solution.
Problem
Calculate the solution to 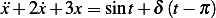 with IC
with IC 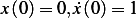 and plot the
solution.
and plot the
solution.
Answer
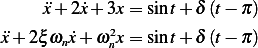
Hence 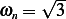 and
and 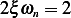 , hence
, hence 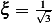
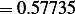 , hence this is underdamped system.
, hence this is underdamped system.
Since 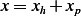 , then
, then
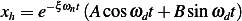
We have 2 particular solutions. The first 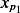 is due to
is due to 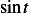 and the second
and the second 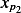 is due to
is due to 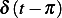 . When the
forcing function is
. When the
forcing function is 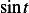 , we guess
, we guess
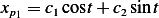
and when the forcing function is 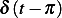 the response is
the response is
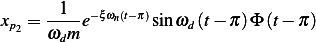
From 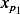 we find
we find 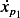 and
and 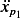 and plug these into
and plug these into 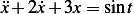 to find
to find 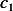 and
and 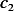 , next we find
, next we find 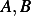 by
using the IC, and then at the end we add the solution
by
using the IC, and then at the end we add the solution 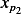 . Notice that
. Notice that 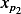 do not enter into the calculation of
do not enter into the calculation of
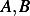 since the impulse
since the impulse 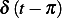 is not effective at
is not effective at 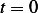 .
.
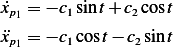
Hence
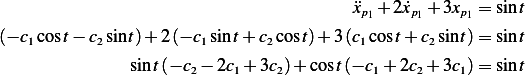
Hence 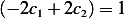 and
and 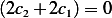 . This results in
. This results in
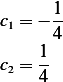
Hence
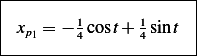
Therefore
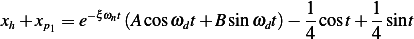
Now we use IC's to find 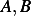 . At
. At 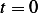 we obtain
we obtain
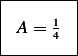
And
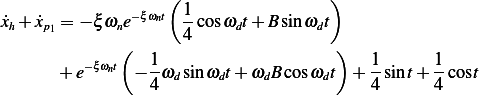
At 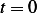 we have
we have
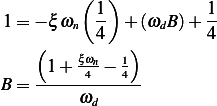
But 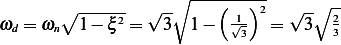 , Hence
, Hence 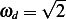 then the above becomes
then the above becomes
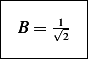
Hence the final solution is
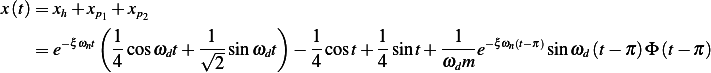
Substitute values for the parameters above we obtain
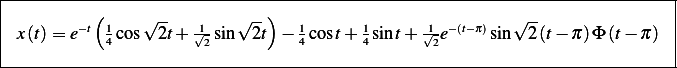
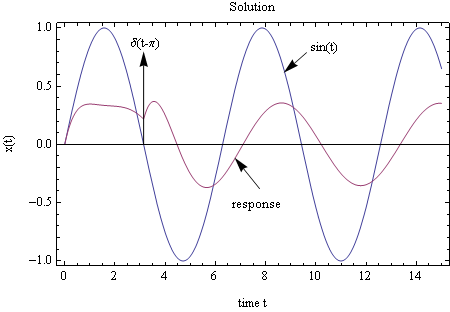
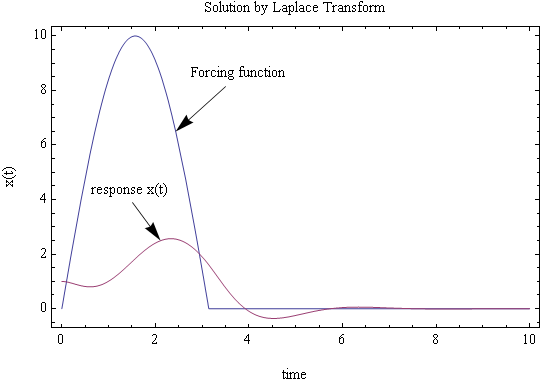
This is a plot of the solution superimposed on the forcing functions
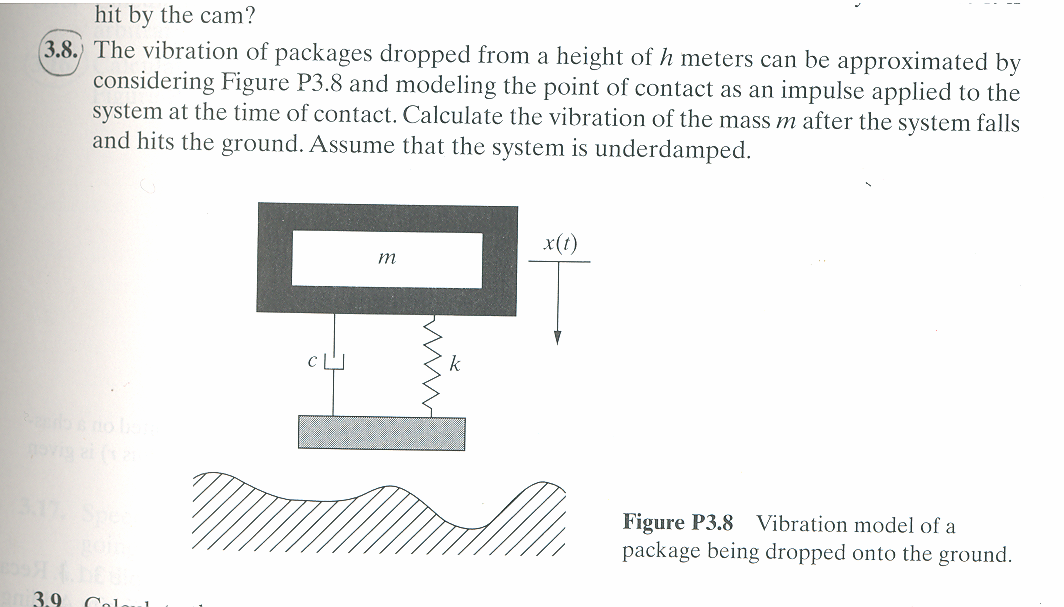
The magnitude of the impulse resulting when the mass hits the ground is given by the change of momentum that occurs. Hence
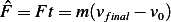
But assuming the mass is dropped from rest, hence 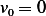 , and
, and 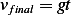 where
where 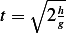 where
where 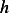 is the
height that mass falls. Hence
is the
height that mass falls. Hence
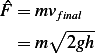
Hence the equation of motion is
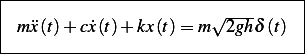
Since underdamped, 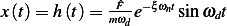 , hence the solution is
, hence the solution is
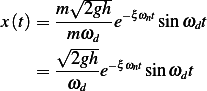
Taking 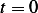 as time of impact.
as time of impact.
Problem
Compute response of the system 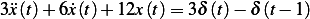 with IC
with IC 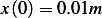 and
and
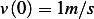 . Plot the response.
. Plot the response.
Answer
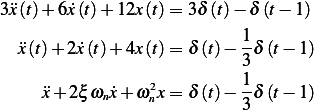
Where 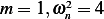 , hence
, hence 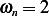 and
and 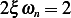 , hence
, hence 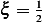 . This is an underdamped system.
. This is an underdamped system.
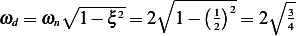 , Hence
, Hence 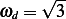
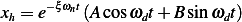
The response due to the forcing function 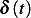 is given by
is given by
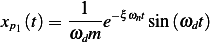
The response due to the other forcing function 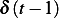 is given by
is given by
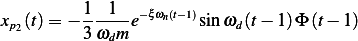
Now we determine 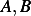 from IC's
from IC's
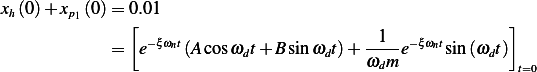
Hence 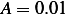 Now to find
Now to find 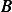
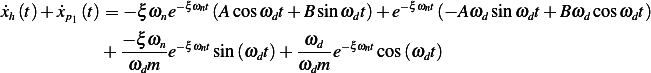
But 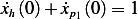 , hence from the above, and noting that
, hence from the above, and noting that 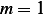
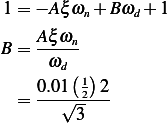
Hence
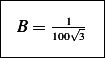
Therefore
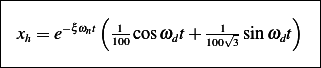
Now we can combine the above solution to obtain the final solution
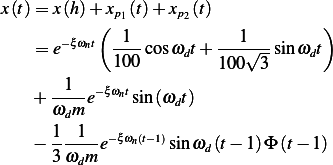
Substitute numerical values for the above parameters, we obtain
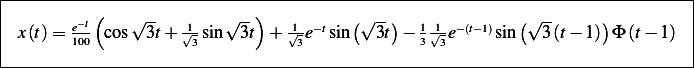
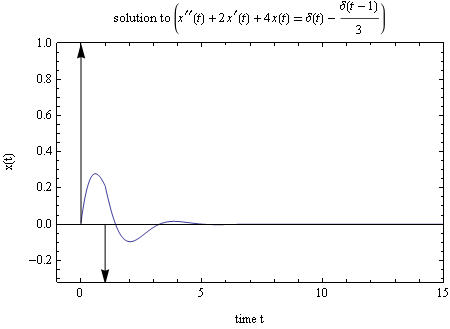
This is a plot of the response
Let the response by 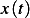 . Hence
. Hence 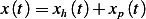 , where
, where 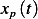 is the particular solution, which is the response
due the the above forcing function. Using convolution
is the particular solution, which is the response
due the the above forcing function. Using convolution
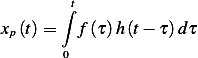
Where 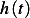 is the unit impulse response of a second order underdamped system which is
is the unit impulse response of a second order underdamped system which is
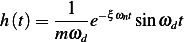
hence
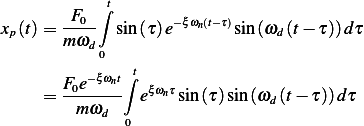
Using ![1
sin Asin B= 2[cos (A − B)− cos(A +B )]](ME93x.png) then
then
![1
sin(τ)sin(ωd(t− τ))= 2-[cos(τ − ωd(t− τ))− cos(τ+ ωd(t− τ))]](ME94x.png)
Then the integral becomes
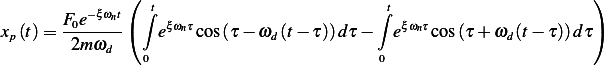
Consider the first integral 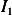 where
where
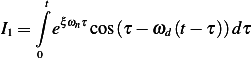
Integrate by parts, where 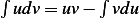 , Let
, Let 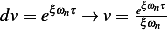 and let
and let
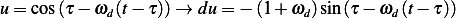 , hence
, hence
Integrate by parts again the last integral above, where 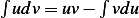 , Let
, Let 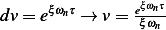 and
let
and
let 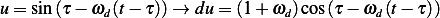 , hence
, hence
Substitute (2) into (1) we obtain
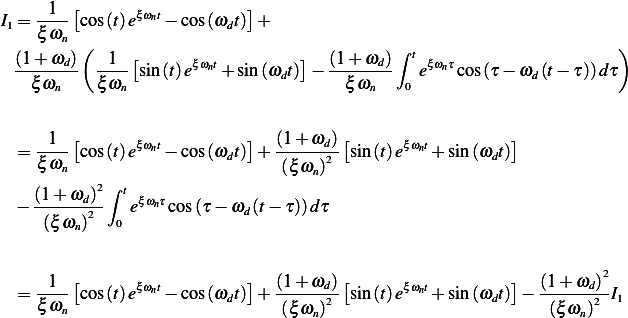
Hence
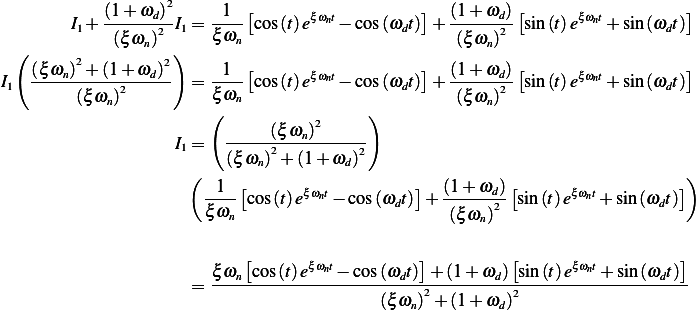
Now consider the second integral 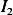 where
where
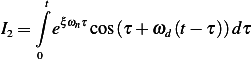
Integrate by parts, where 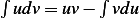 , Let
, Let 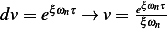 and let
and let
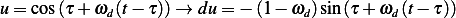 , hence
, hence
Integrate by parts again the last integral above, where 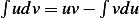 , Let
, Let 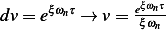 and
let
and
let 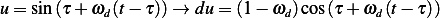 , hence
, hence
Substitute (4) into (3) we obtain
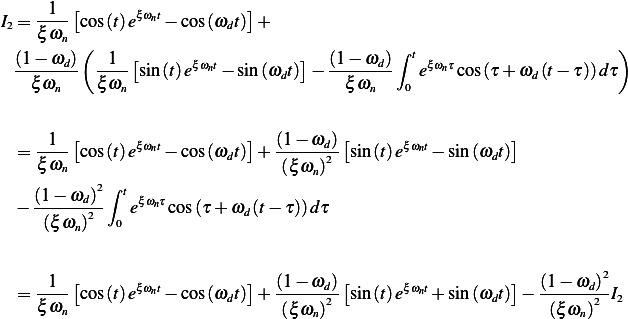
Hence
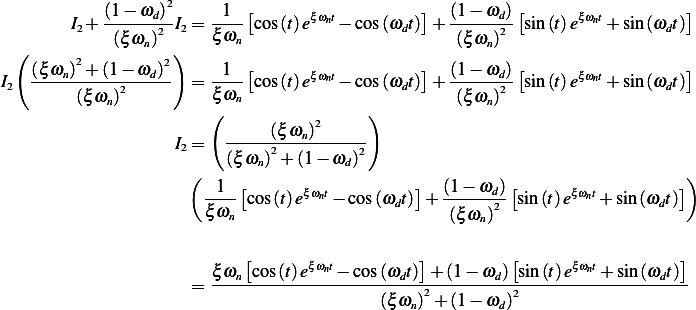
Using the above expressions for 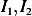 , we find (and multiplying the solution by
, we find (and multiplying the solution by 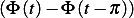 since
the force is only active from
since
the force is only active from 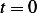 to
to 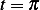 , we obtain
, we obtain
Hence 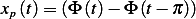
![[ ( ) ]
-F0-e−ξωnt ξωn[cos(t)eξωnt−cos(ωdt)]+(1+ωd)[sin(t)eξωnt+sin(ωdt)]-− ξωn[cos(t)eξωnt−cos(ωdt)]+(1−ωd)[sin(t
2mωd (ξωn)2+(1+ωd)2 (ξωn)2+(1−ωd)2](ME126x.png)
But
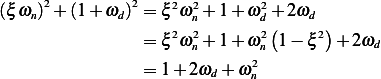
and
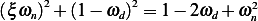
Hence  can now be written as
can now be written as
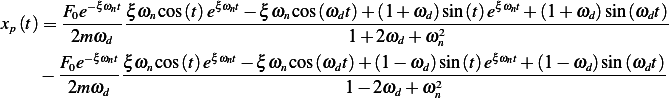
And
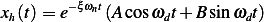
Hence the overall solution is
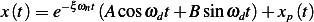
The above solution is a bit long due to integration by parts. I will not solve the same problem using Laplace transformation method. The differential equation is
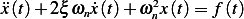
Take Laplace transform, we obtain (assuming 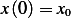 and
and 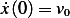 )
)
Now we find Laplace transform of 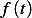
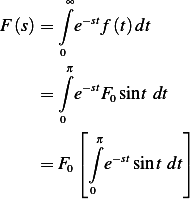
Integration by parts gives
![[ −πs]
F (s)= F0 1-+-e--
1 + s2](ME139x.png) | (8) |
Substitute (8) into (7) we obtain
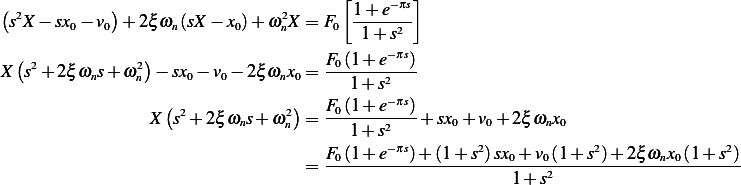
Hence
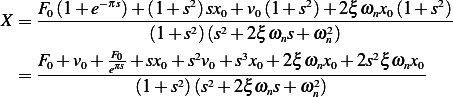
Now we can use inverse Laplace transform on the above. It is easier to do partial fraction decomposition
and use tables. I used CAS to do this and this is the result. I plot the solution 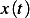 . I used the following
values to be able to obtain a plot
. I used the following
values to be able to obtain a plot 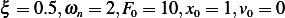

The acceleration 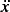 of the mass is measured w.r.t. to the inertial frame, but the spring length is measured relative
to the ground which is moving with displacement
of the mass is measured w.r.t. to the inertial frame, but the spring length is measured relative
to the ground which is moving with displacement 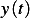 , hence the equation of motion of the mass
, hence the equation of motion of the mass  is given
by
is given
by
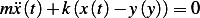
Therefore
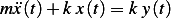 | (1) |
Where 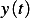 is given as
is given as
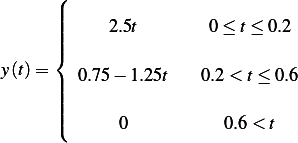
The solution to (1) is given by 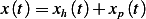 where
where 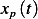 can be found using convolution, and
can be found using convolution, and 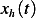 is
as usual given by
is
as usual given by
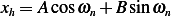
Let us first find 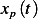 . Note that the impulse response
. Note that the impulse response 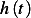 to undamped system is given by
to undamped system is given by
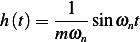
Hence for 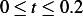 ,
,
Integration by parts, 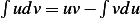 where
where  ,
, 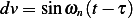 , hence
, hence 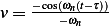 , therefore
(2) becomes
, therefore
(2) becomes
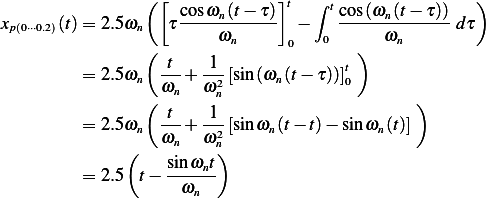
For 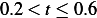
For the first integral in (3), we obtain
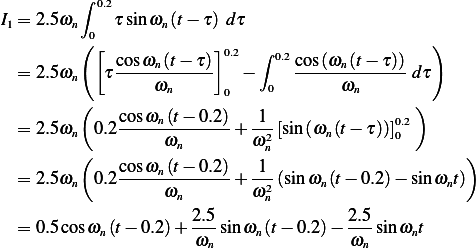
For the second integral in (3) we obtain
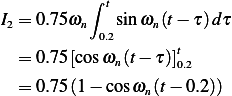
For the third integral in (3) we obtain
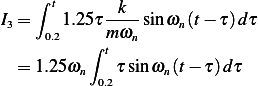
Integration by parts gives
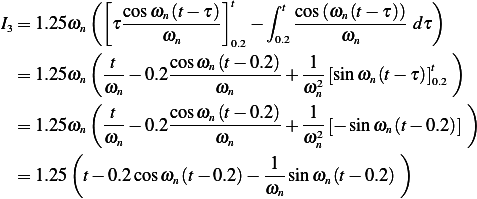
Hence
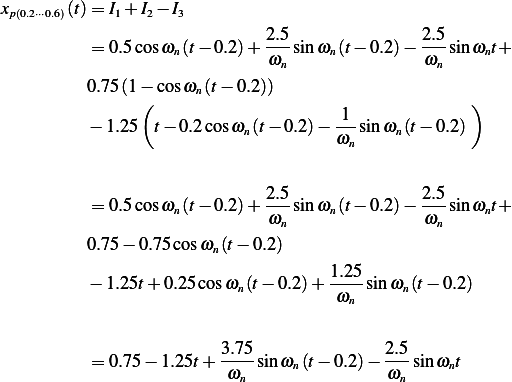
For 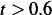
For the first integral in (4), we obtain
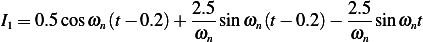
For the second integral in (4) we obtain
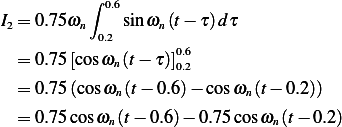
For the third integral in (4) we obtain
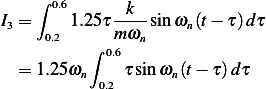
Integration by parts gives
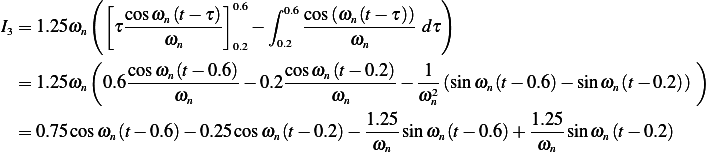
Hence
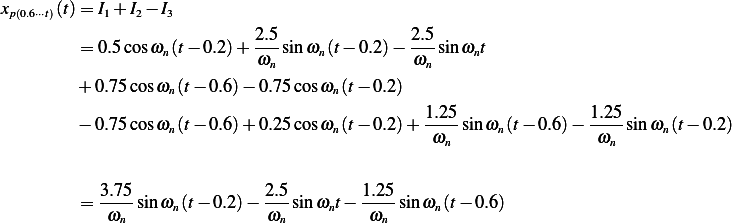
Hence, the overall response is, assuming zero initial conditions, is given by
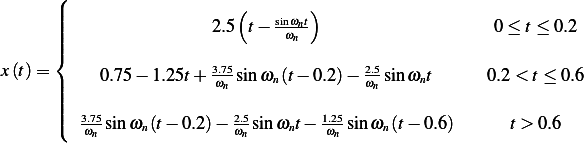
Noting that 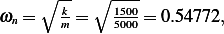 the above becomes
the above becomes
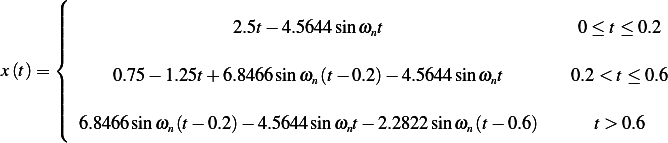
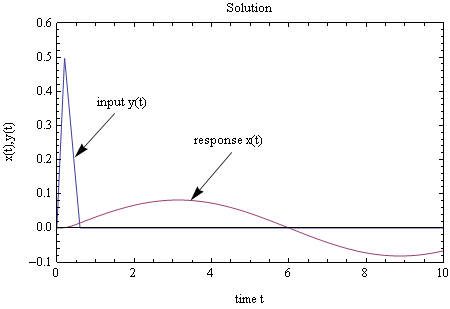
This is a plot of the solution superimposed on top of the forcing function
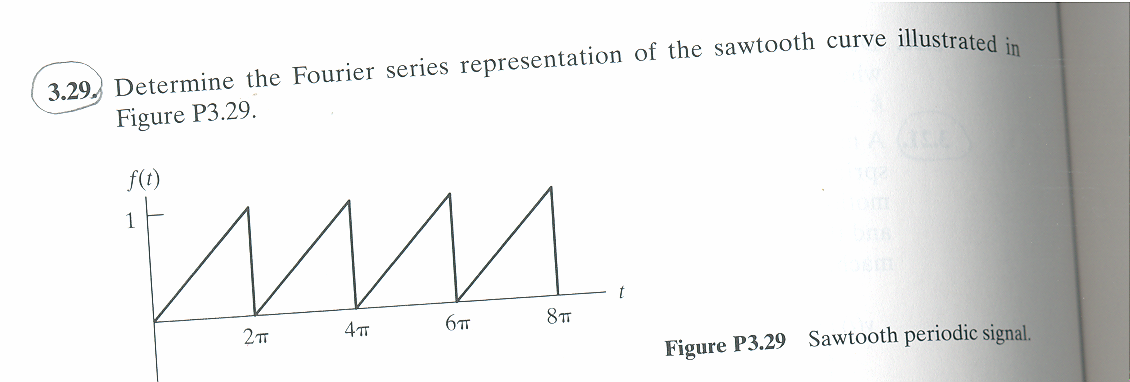
Let 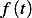 be the function shown above. Let
be the function shown above. Let 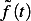 be its approximation using Fourier series. Hence
be its approximation using Fourier series. Hence
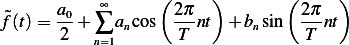
Where 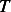 is the period of
is the period of 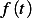 and
and
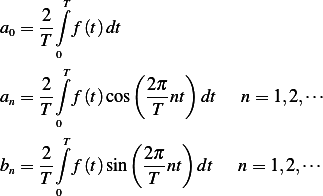
For 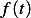 we see that
we see that 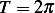 and
and 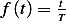 for
for 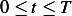 , hence
, hence
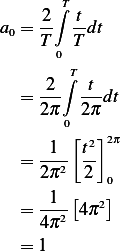
And
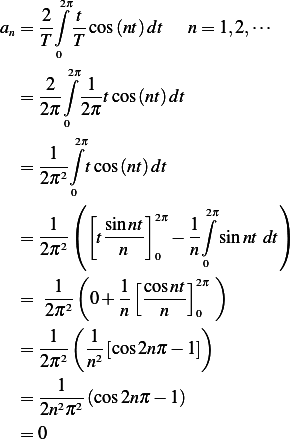
And
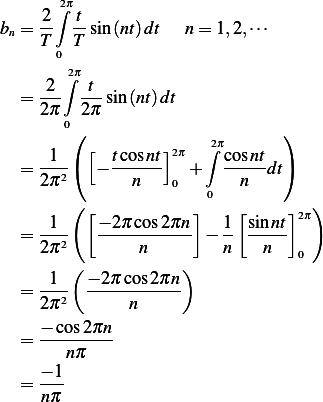
Hence
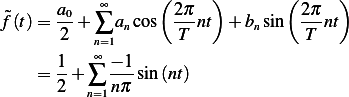
These are few terms in the series
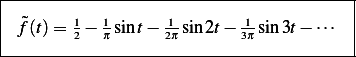
This is a plot of the above for increasing number of 
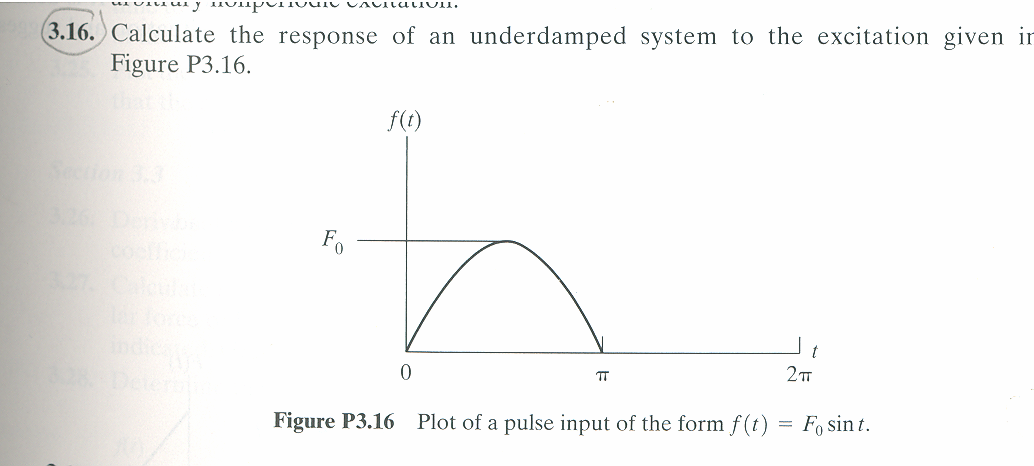
Problem
Solve the following system using Laplace transform 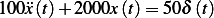 where the units are in
Newtons and the initial conditions are both zero.
where the units are in
Newtons and the initial conditions are both zero.
Answer
Divide the equation by 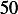 we obtain
we obtain
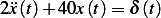
Let 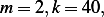 hence the equation becomes
hence the equation becomes
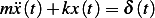
Applying Laplace transform
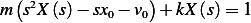
But due to zero initial conditions, the above simplifies to
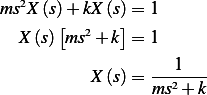
From tables, the inverse Laplace transform of 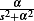 is
is 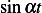 , but
, but
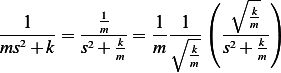
Hence, letting 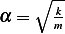 we see that inverse laplace transform of
we see that inverse laplace transform of 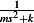 is the same as the inverse laplace
transform of
is the same as the inverse laplace
transform of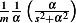 which is
which is 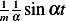
But 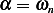 , hence
, hence
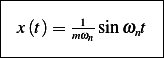
or
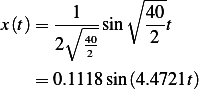
Problem
Calculate the response spectrum of an undamped system to the forcing function
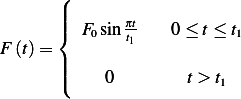 assuming zero initial conditions.
assuming zero initial conditions.
Answer
Solution sketch: Find the response 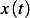 of the system to the above input. Then find
of the system to the above input. Then find 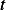 where this response
is maximum, call this
where this response
is maximum, call this 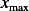 , then plot
, then plot 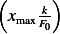 vs.
vs. 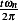
The system EQM is
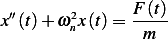
For 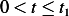 ,
,
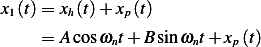
Guess 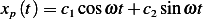 , hence
, hence 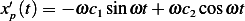 and
and 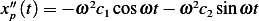 ,
hence substitute these into the EQM and compare, we obtain
,
hence substitute these into the EQM and compare, we obtain
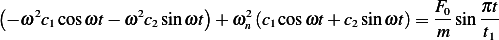
The input is half sin where 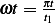 , hence
, hence 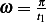
 hence the above becomes
hence the above becomes
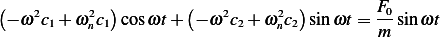
Hence 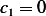 and
and 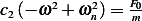 or
or 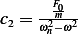
 Then the solution becomes
Then the solution becomes
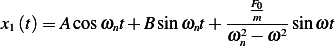
And since 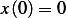 then
then 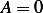 and take derivative we obtain
and take derivative we obtain
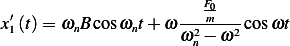
And since 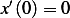 then the above results in
then the above results in
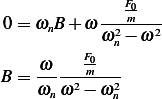
Hence the solution becomes
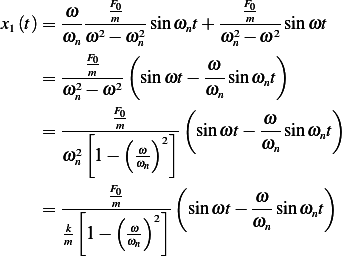
Hence
![F0 ( ω )
x1(t)= [----k(--)2] sin ωt− ---sin ωnt 0 < t ≤ t1
1 − ωω- ωn
n](ME243x.png) | (1) |
Now we need to find where the maximum is. Take derivative, and set it to zero, we obtain
 = 0
1 k ( ω-)2 n
1 − ωn](ME244x.png)
For 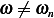 , we need to solve
, we need to solve
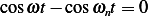
Using 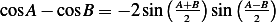 , then the above becomes
, then the above becomes
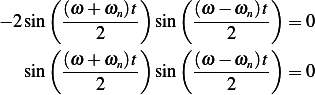
Hence, either 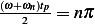 or
or 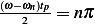 for
for 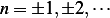 or the time
or the time 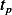 which makes the maximum
which makes the maximum
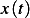 is one of the following
is one of the following
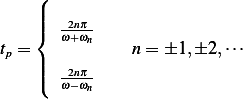
We now need to find which one of the above 2 solution gives a larger maximum. Using the first solution
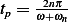 , then (1) becomes
, then (1) becomes
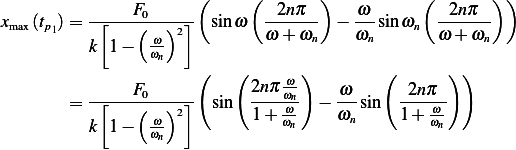
And at 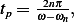 then (1) becomes
then (1) becomes
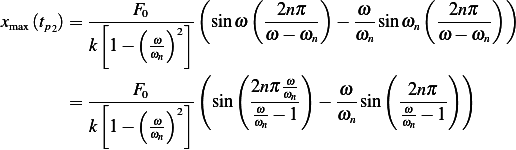
Need now to find which of the above is larger. Let us take the difference and see if the result is positive or negative (is there an easier way?)
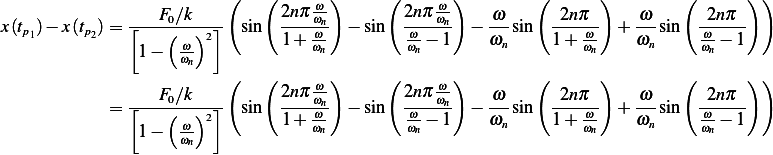
Not sure how to continue. Now let us look at 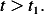 The solution here is
The solution here is
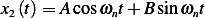
But with IC given by 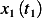 and
and 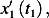 hence from (1)
hence from (1)
![F ( )
-----0k----- -ω-
x1(t1)= [ ( ω)2] sinωt1− ωn sin ωnt1
1− ωn](ME264x.png)
and
![′ F0 -----1-----
x1(t1)= k [ ( )2] (ω cosωt1− ω cosωnt1)
1− ωωn](ME265x.png)
Hence
![( )
x2(t1)= A cosωnt1+ B sin ωnt1 = [--F0(∕k-)-] sinωt1 − ω-sinωnt1
1− ω- 2 ωn
ωn](ME266x.png) | (3) |
And

1 − ω- 2
ωn](ME267x.png) | (4) |
We need to solve (3) and (4) for 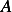 and
and 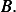 Combining (3) and (4) we obtain
Combining (3) and (4) we obtain
![⌊ ⌋⌊ ⌋ ⌊ ( ) ⌋
| [-F0∕k-2] sin ωt1− ω-sin ωnt1 |
|| cosωnt1 sinωnt1 |||| A|| || 1−(ωωn) ωn ||
|⌈ |⌉|⌈ |⌉ = | |
− ωn sinωnt ωn cosωnt B ⌈[--F0∕k2](ω cosωt1− ω cosωnt1)⌉
1−( ωωn)](ME270x.png)
This is in the form 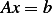 , solve for
, solve for 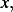 we obtain
we obtain
![⌊ ⌋ ⌊ ⌋⌊ ⌋( )
( ω )
||A|| 1 || ωncosωnt1 − sinωnt1|||| sinωt1− ωn sinωnt1 ||| F0∕k |
|⌈ |⌉ = ω-|⌈ |⌉|⌈ |⌉|( [----(--)2]|)
B n ωn sinωnt cosωnt (ω cosωt1− ω cosωnt1) 1 − ωωn](ME273x.png)
Hence
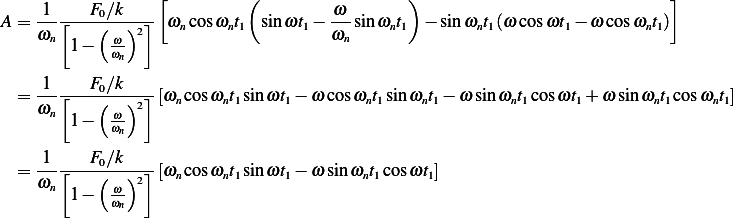
And
Ask about the above, why can't I get the answer shown in notes?
To find the response 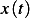 use convolution. Since this is an undamped system, then the impulse response
is
use convolution. Since this is an undamped system, then the impulse response
is
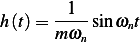
Hence, for 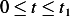
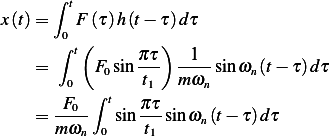
Using 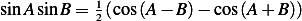 , then
, then
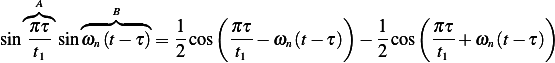
Hence the convolution integral becomes
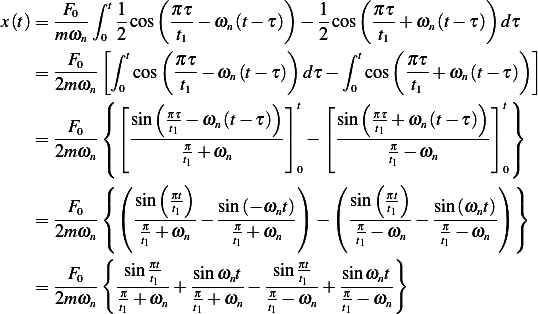
And for 
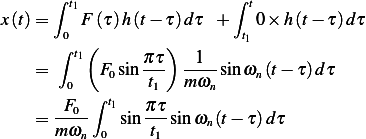
As was done earlier, perform integration by parts, we obtain
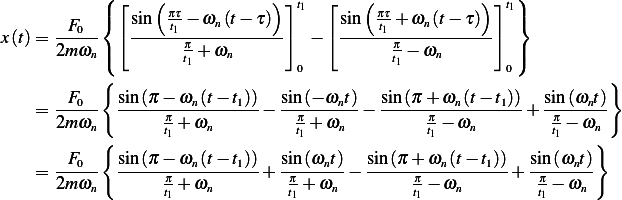
But 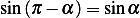 and
and 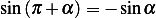 , hence the above becomes
, hence the above becomes
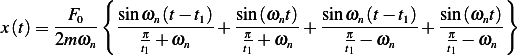
Therefore, the final solution is
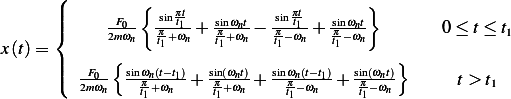 | (1) |
We can simplify the above more as follows
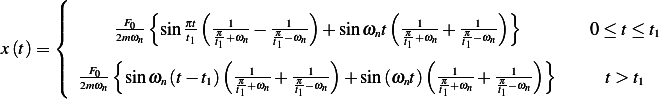 | (1) |
Hence
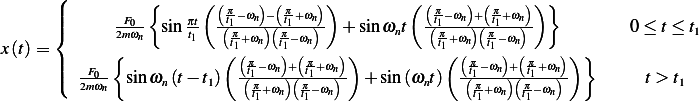 | (1) |
Hence
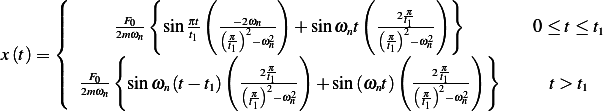 | (1) |
or
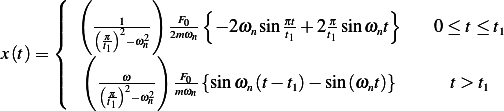 | (1) |
Hence
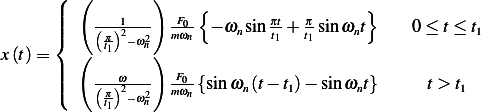 | (1) |
To find where  is, we need to find
is, we need to find 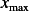 . Take the derivative, we obtain
. Take the derivative, we obtain
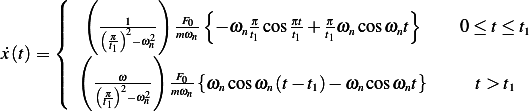
Now let 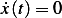 for
for  to find
to find 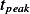 .
.
But
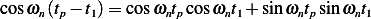
Substitute the above into (2) we obtain
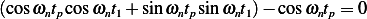
Divide by 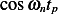
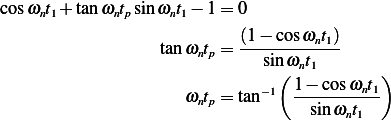
Hence, the hypotenuse is 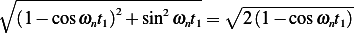 and so
and so 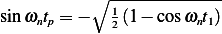 and
and 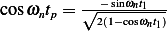 and using these into (1) we find
and using these into (1) we find 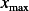 when
when 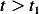 as
as
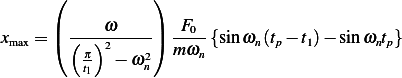
But 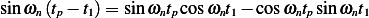 , hence
, hence
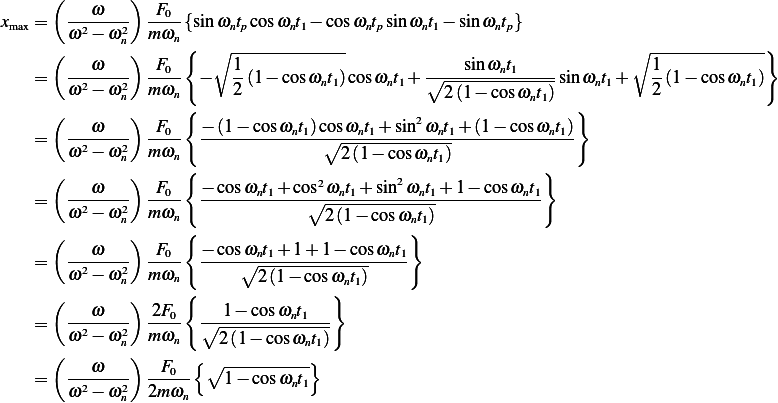
Hence
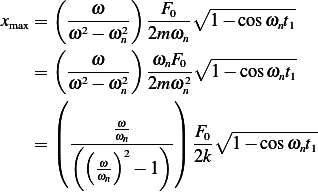
Hence
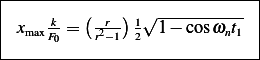
Where 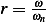
A plot of 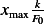 vs.
vs.  gives the response spectrum
gives the response spectrum
Problem Calculate the compliance transfer function for a system described by 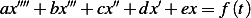 where
where 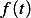 is the input and
is the input and 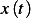 is the displacement.
is the displacement.
Answer
Take Laplace transform (assuming zero IC) we obtain
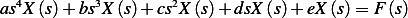
Hence
![[ ]
X (s) as4+ bs3+ cs2+ ds+ e = F (s)](ME323x.png)
Hence
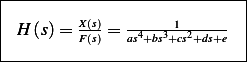
Problem
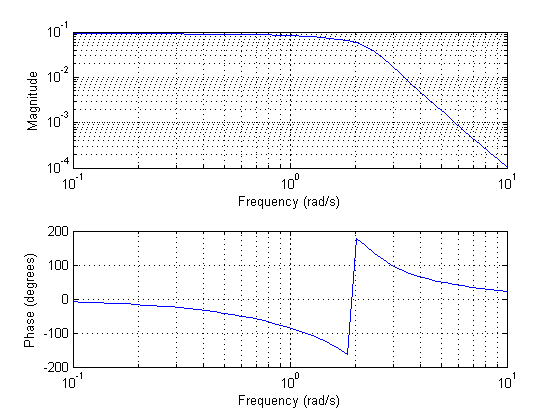
Calculate the frequency response function for the system of problem 3.49 for 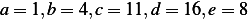
Answer
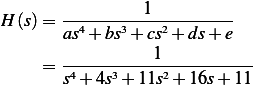
Let 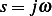
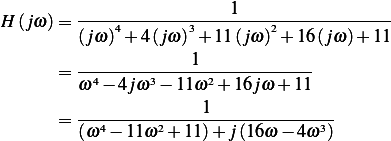
Hence
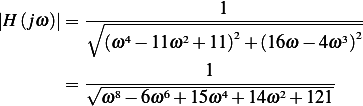
and
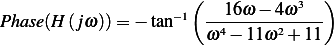
This is a plot of the magnitude and phase