
Taking displacement along the x-direction shown to be from the static equilibrium position, then applying
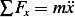 along the shown
along the shown 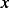 direction, we obtain
direction, we obtain
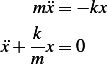
which is the equation of motion. To obtain the natural frequency, we consider free vibration 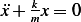 ,
which implies that
,
which implies that 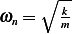 , hence we see that the natural frequency is independent of
, hence we see that the natural frequency is independent of 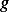
We see that gravity has no effect on the spring mass system, this is because we use 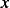 to be from the static
equilibrium position of the spring.
to be from the static
equilibrium position of the spring.
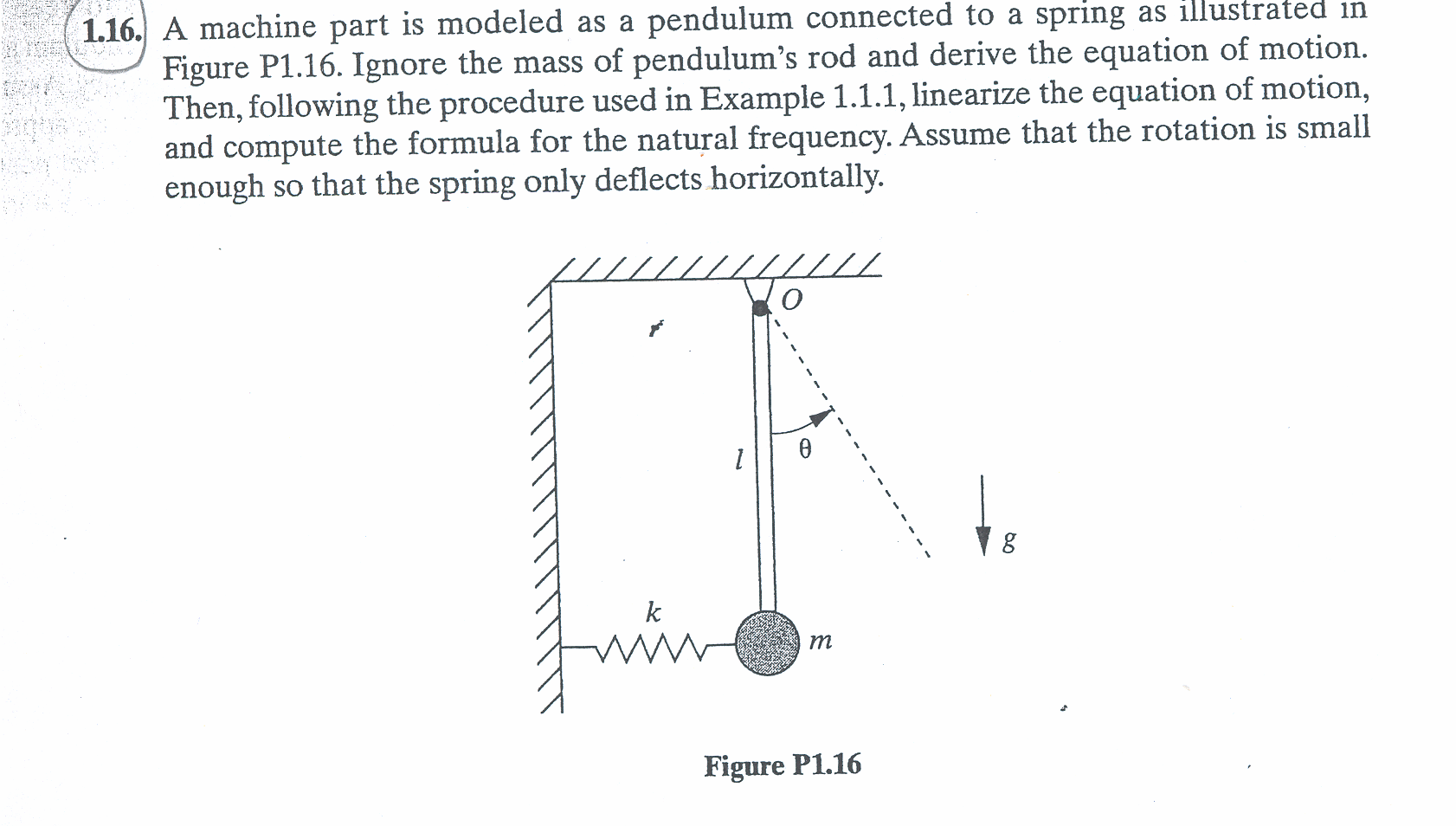
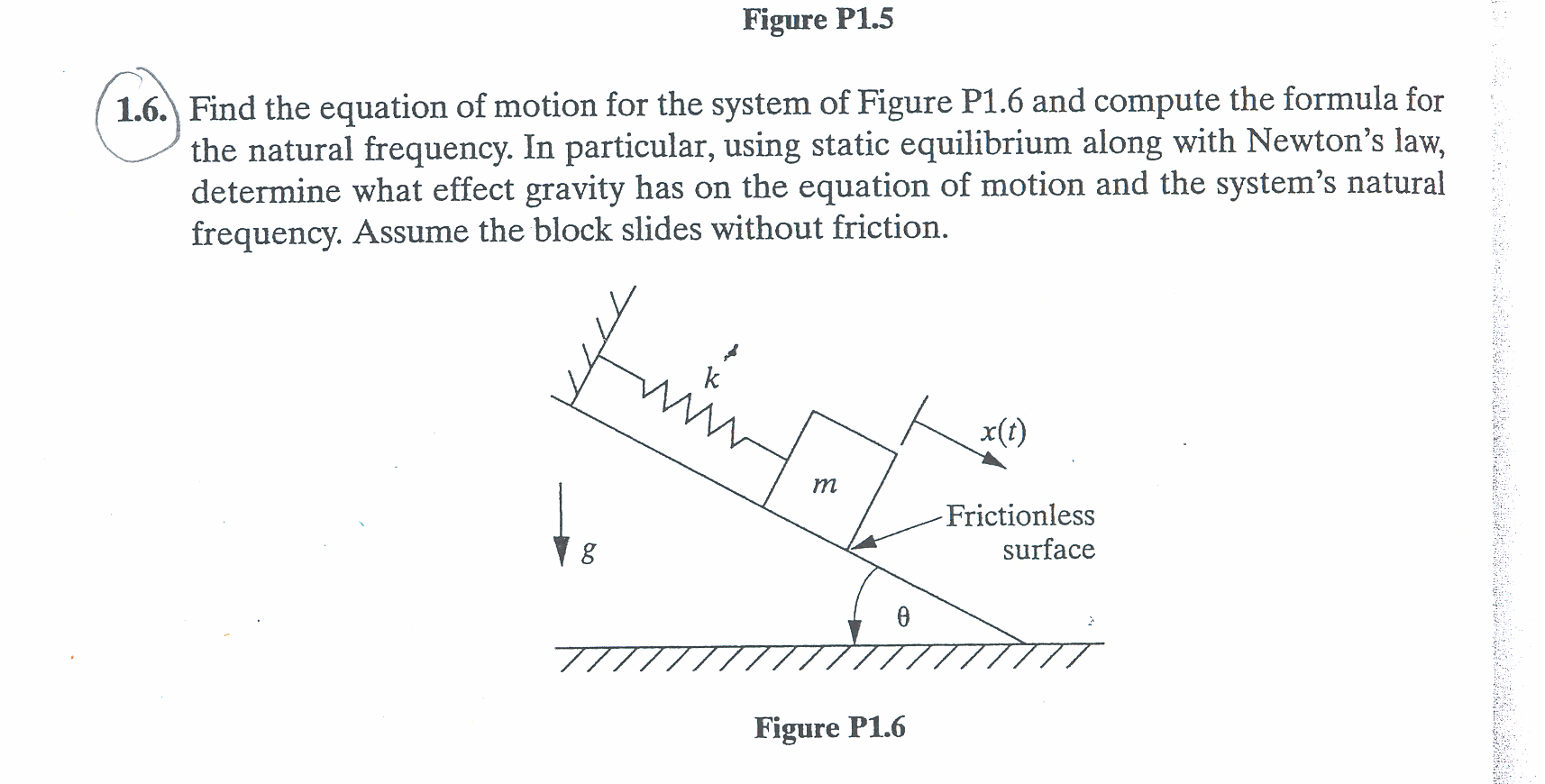
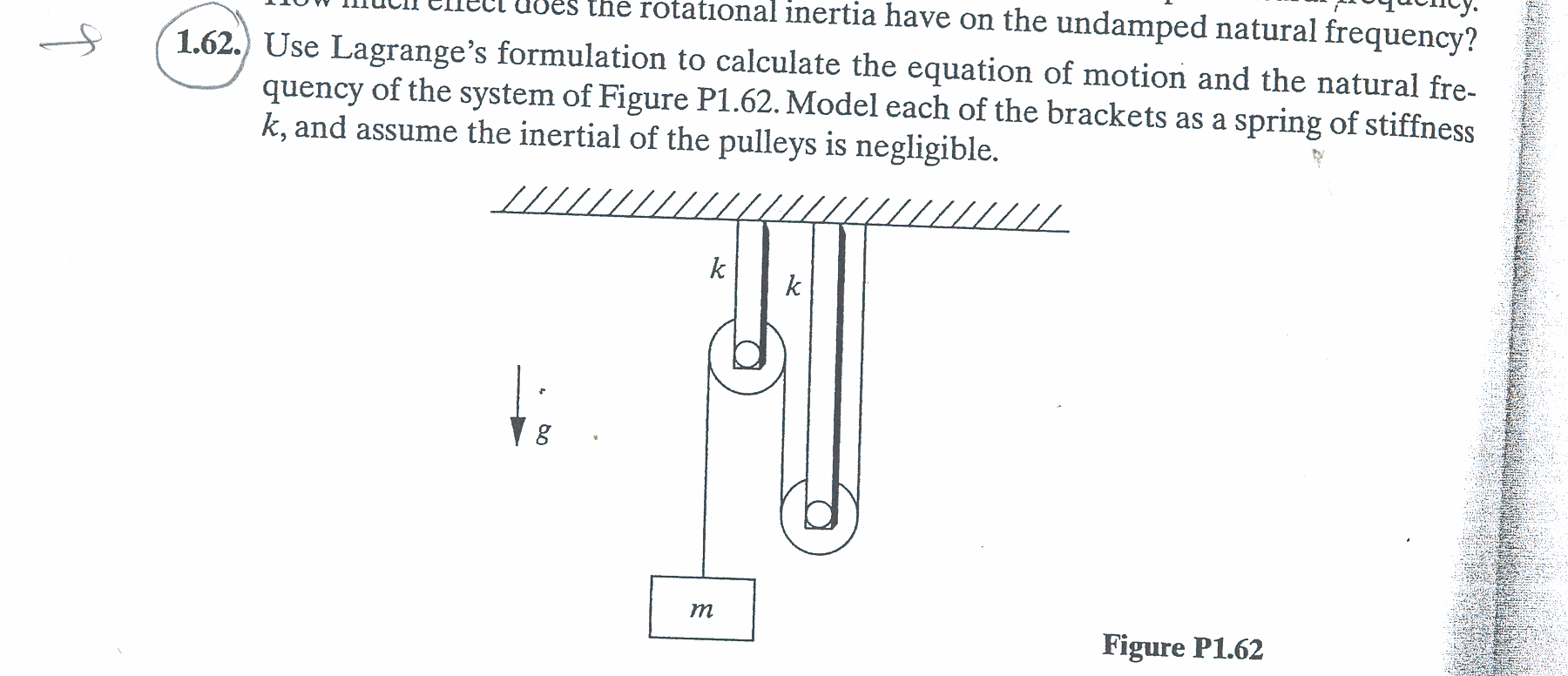
First we need to derive the equation of motion. Considering the following diagram
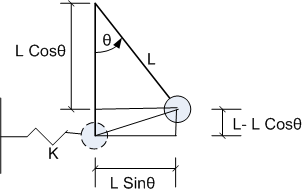
Using as generalized coordinates  , we obtain
, we obtain
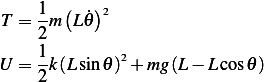
Notice that in the calculation of 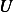 above, we assumed that the spring stretches by
above, we assumed that the spring stretches by 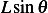 in the horizontal
direction only, which we are allowed to do for small
in the horizontal
direction only, which we are allowed to do for small 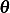 .
.
Now we can find Lagrangian
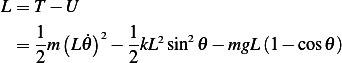
Hence the equation of motion is
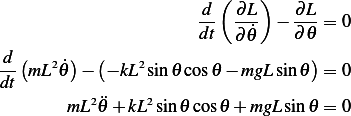
The above is nonlinear equation. Linearize around 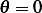 (equilibrium point) using Taylor series, and for
small
(equilibrium point) using Taylor series, and for
small 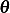 we obtain
we obtain 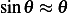 and
and 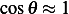 , hence the above becomes
, hence the above becomes
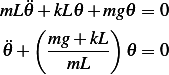
Hence effective 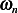 can be found from
can be found from
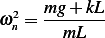
Hence
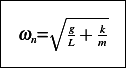
Compare the above to the natural frequency of pendulum with no spring attached which is 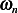 =
=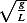 , we
can see the effect of adding a spring on the natural frequency: The more stiff the spring is, in other words, the
larger
, we
can see the effect of adding a spring on the natural frequency: The more stiff the spring is, in other words, the
larger 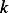 is, the larger
is, the larger 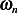 will become, and the smaller the period of oscillation will be. We conclude that a
pendulum with a spring attached to it will always oscillate with a period which is smaller than the
same pendulum without the spring attached. This makes sense as a mass with spring alone has
will become, and the smaller the period of oscillation will be. We conclude that a
pendulum with a spring attached to it will always oscillate with a period which is smaller than the
same pendulum without the spring attached. This makes sense as a mass with spring alone has
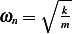
We need to solve 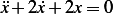 for
for 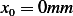 and
and 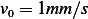
The characteristic equation is 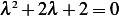 which has roots
which has roots 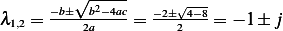
Hence the solution is
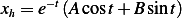
is the general solution. Now we use I.C. to find 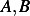 . When
. When 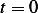
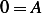
Hence 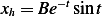 , and
, and 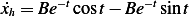 and at
and at 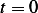 , we obtain
, we obtain 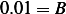
Then
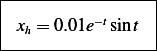
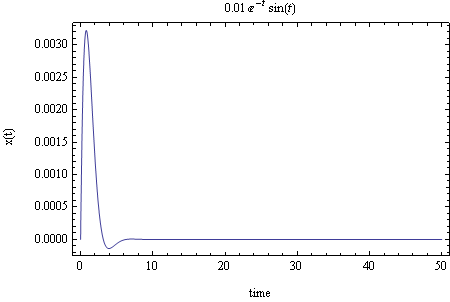
This is a plot of the solution for  up to 50 seconds
up to 50 seconds
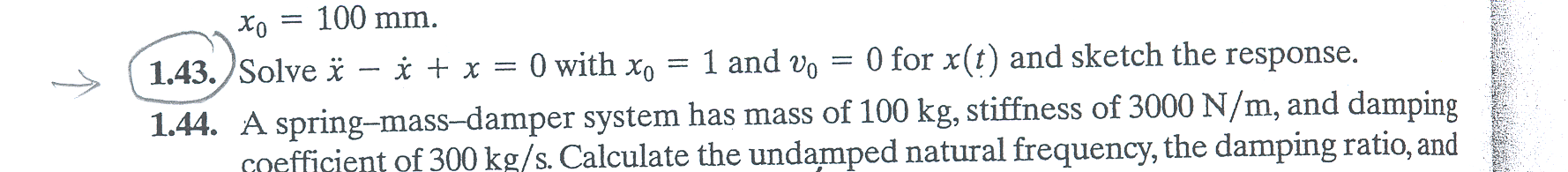
We need to solve 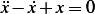 for
for 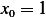 and
and 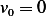
The characteristic equation is 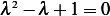 which has roots
which has roots 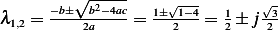
Hence the solution is
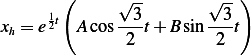
is the general solution. Now we use I.C. to find  . When
. When 
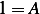
Hence 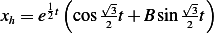 , and
, and
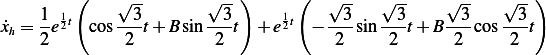
and at 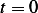 , we obtain
, we obtain
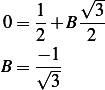
Hence
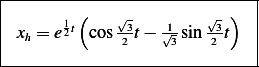
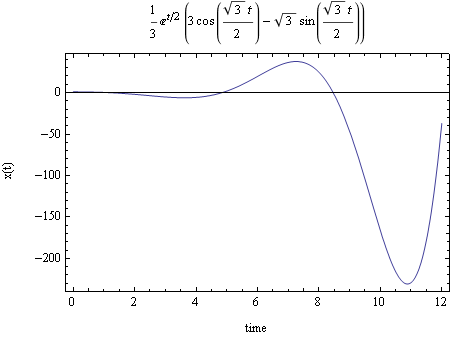
This is a plot of the solution for  up to 12 seconds
up to 12 seconds
This is a single degree of freedom linear system. Assume 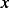 from static equilibrium, then (using parallel springs)
we obtain
from static equilibrium, then (using parallel springs)
we obtain
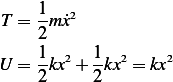
Hence 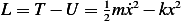 and the Lagrangian equation is
and the Lagrangian equation is
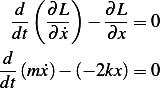
Hence equation of motion is
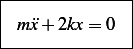
Solution
Part(a)
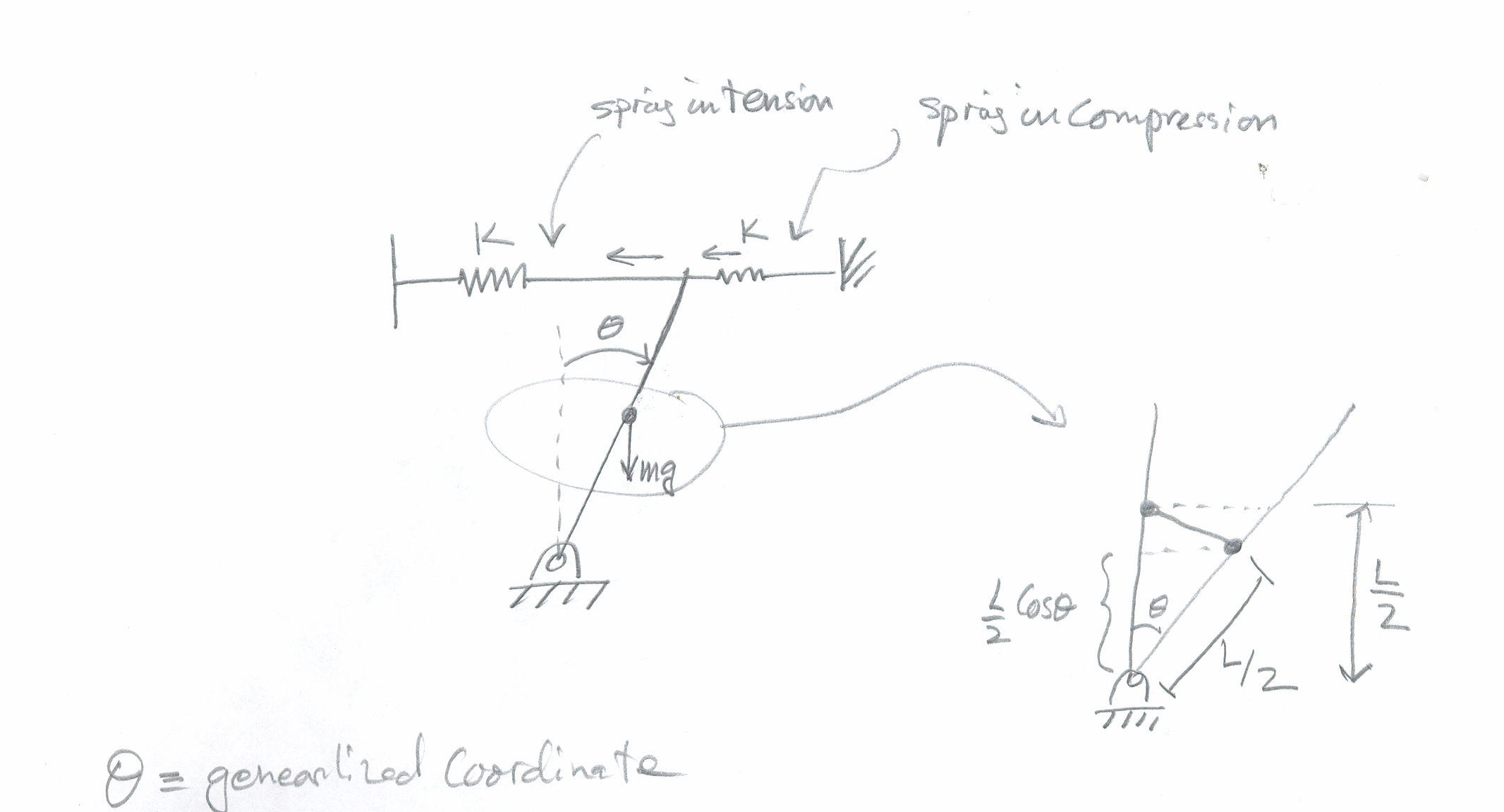
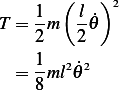
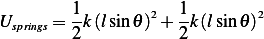
Assuming small angle oscillation, 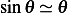 , hence
, hence
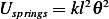
and for the mass, since it losses potential, we have
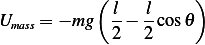
Hence Lagrangian 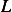 is
is
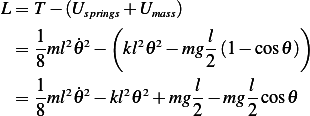
Now find the Lagrangian equation
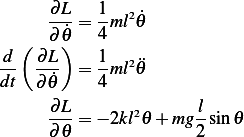
Hence
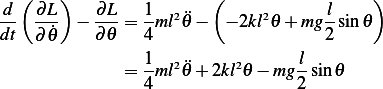
And the equation of motion is
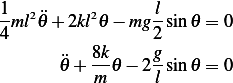
Linearize by setting 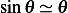 we obtain equation of motion
we obtain equation of motion
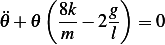 | (1) |
Hence
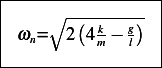
Part (b)
To discuss stability, we need to determine the location of the roots of the characteristic equation of the homogeneous EQM, hence from equation (1), we see that
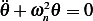
And assuming solution 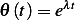 leads to the characteristic equation
leads to the characteristic equation
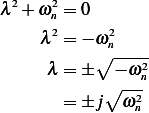
Since 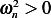 , then
, then
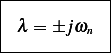
Since roots of the characteristic equation on the imaginary axis, this is a marginally stable system
regardless of the values of 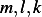 .
.
Since we are looking at the linearized system, there is only one equilibrium point, and the system is either
stable or not. Here we found it is marginally stable. The effect of changing 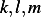 is to change the period of
oscillation around the equilibrium point.
is to change the period of
oscillation around the equilibrium point.