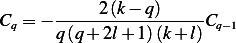
A CLASS ASSIGNED PROBLEM FOR PHYSICS 555ASPRING 2008. CSUF
BY NASSER ABBASI
Show that the recurence formula
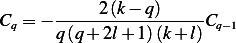 | (1) |
can be written as
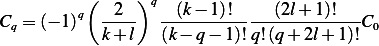 | (2) |
Proof by induction on 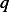 . For
. For 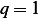 , equation (1) becomes
, equation (1) becomes
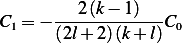
and equation (2) becomes
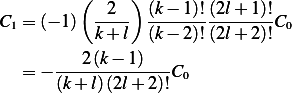
Hence it is true for 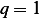 . Now assume it is true for
. Now assume it is true for 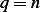 , in otherwords, assume that
, in otherwords, assume that
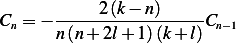 | (3) |
implies
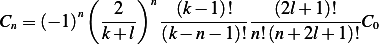 | (4) |
Now for the induction step. we need to show that it is true for 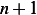 , i.e. given (4) is true, we need to show
that, by replacing
, i.e. given (4) is true, we need to show
that, by replacing  by
by 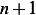 in the above, that
in the above, that
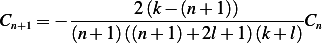 | (5) |
implies
We start with (5), and replace the 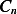 term with what we assumed to be true from (4), hence (5) can be
rewritten as
term with what we assumed to be true from (4), hence (5) can be
rewritten as
![Cnfrom(4)
◜[------(-----)n-----◞◟------------------]◝
Cn+1 = −--------2(k−-(n+-1))------- (− 1)n --2- --(k−-1)!- --(2l+-1)!--C0
(n + 1)((n +1 )+ 2l+1 )(k + l) k + l (k− n − 1)! n!(n + 2l+ 1)!](HW18x.png)
Simplify the above leads to
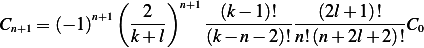
Which is (6). Therefore, the relationship is true for any  . QED
. QED