
HW problem 5.7 Math 504. Spring 2008. CSUF
by Nasser Abbasi
Problems

Part(A)
Let
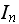 be an indicator variable defined
as
be an indicator variable defined
as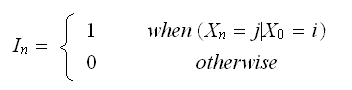 Hence
Hence
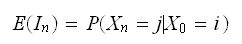 Now we see that
Now we see that
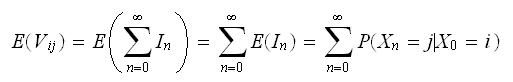 Now, let
Now, let
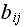 be entry in matrix
be entry in matrix
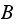 where
where
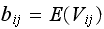 ,
then the above can be written
as
,
then the above can be written
as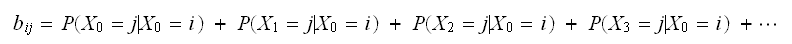 Which is the same as
writing
Which is the same as
writing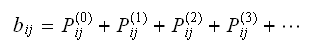 When
When
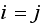 ,
then
,
then
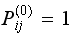 otherwise it is
otherwise it is
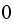 .
Hence
.
Hence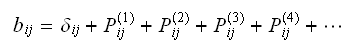 Let the set of transient states be
Let the set of transient states be
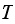 ,
and using chapman-kolmogorov, the above can be written
as
,
and using chapman-kolmogorov, the above can be written
as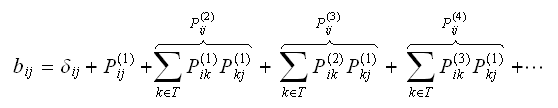 But
But
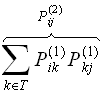 is multiplying the
is multiplying the
 row of the
row of the
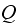 matrix by the
matrix by the
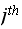 column of the
column of the
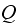 matrix. which is the
matrix. which is the
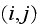 entry of the matrix
entry of the matrix
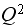 ,
and
,
and
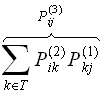 is multiplying the
is multiplying the
 row of the
row of the
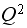 matrix we just obtained, by the
matrix we just obtained, by the
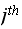 column of the
column of the
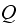 matrix, which is the
matrix, which is the
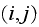 entry of the matrix
entry of the matrix
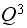 .
Continue this way, we obtain that
.
Continue this way, we obtain that
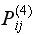 is the entry
is the entry
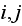 in matrix
in matrix
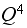 and so on.
and so on.
Hence we see that
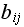 is the
is the
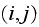 entry of a matrix resulting from
entry of a matrix resulting from
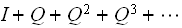 QED.
QED.
Part(B) From part(A), we obtained that
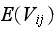 is the
is the
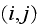 entry in the matrix resulting from the sum
entry in the matrix resulting from the sum
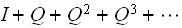 .
Since this is a
.
Since this is a
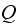 matrix, then we know its elements will all go to zero an
matrix, then we know its elements will all go to zero an
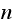 gets very large, so this is a convergent sum, hence
gets very large, so this is a convergent sum, hence
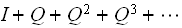 .
.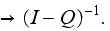 Therefore
Therefore
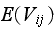 is the
is the
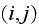 entry in the matrix
entry in the matrix
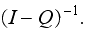
Part(A) I solve this part in 2 ways, first by conditioning on next state, as required, and then by the counting method explained in the lecture.
by conditioning on next state. Let
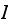 be the set of all states.
Then
be the set of all states.
Then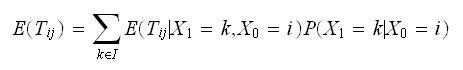 But by Markov property, chain state on next step depends only on current
state. Hence
But by Markov property, chain state on next step depends only on current
state. Hence
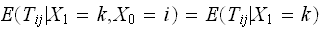 and also since
and also since
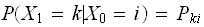 then (1) can be written
as
then (1) can be written
as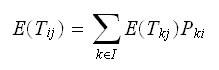 Now, when
Now, when
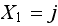 ,
then
,
then
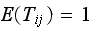 since chain already in state
since chain already in state
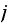 after one step. Therefore (2) can be rewritten
as
after one step. Therefore (2) can be rewritten
as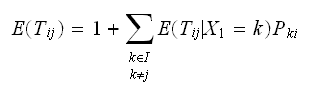 But
But
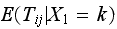 is the same as writing
is the same as writing
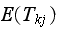 , so the above
becomes
, so the above
becomes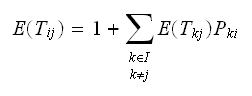 Using the notation shown in the problem, the above becomes
Using the notation shown in the problem, the above becomes
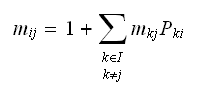 QED.
QED.
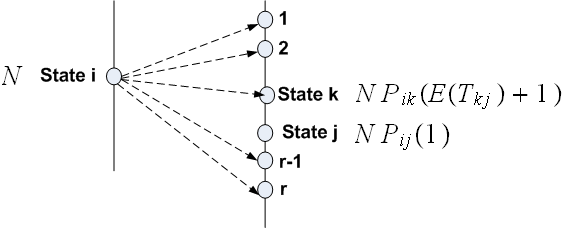
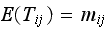 and
and
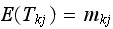 )
)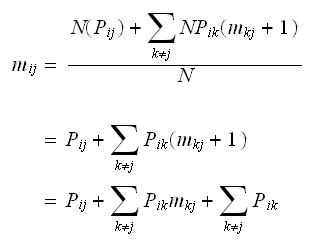 But
But
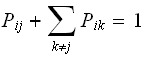 hence the above
becomes
hence the above
becomes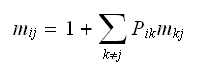
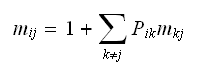 Multiply both sides by
Multiply both sides by
 and
obtain
and
obtain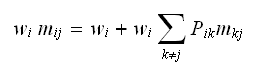 Sum over all possible states
Sum over all possible states
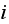 and
obtain
and
obtain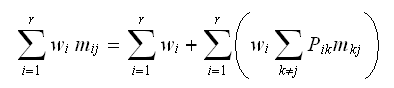 But
But
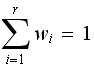 and
and
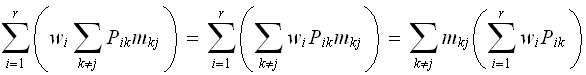 ,
hence (2)
becomes
,
hence (2)
becomes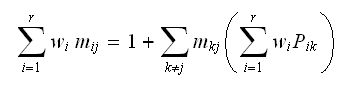 Now, since
Now, since
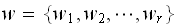 is the stationary state vector, then it satisfies the following
relation
is the stationary state vector, then it satisfies the following
relation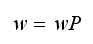 Where
Where
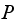 is the one step probability transition matrix. The solution to the above is
given
by
is the one step probability transition matrix. The solution to the above is
given
by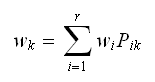 Where
Where
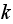 is any state. Using (4) into RHS of (3), we can rewrite (3)
as
is any state. Using (4) into RHS of (3), we can rewrite (3)
as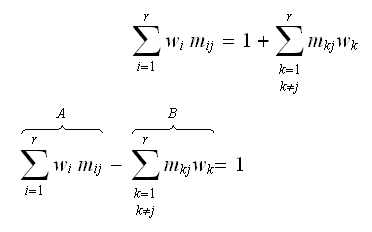 Now looking at the LHS, we see that the first sum labeled
Now looking at the LHS, we see that the first sum labeled
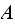 counts for all the
counts for all the
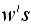 and the second sum labeled
and the second sum labeled
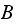 also counts for all the
also counts for all the
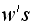 except for the
except for the
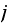 term. Hence if we subtract
term. Hence if we subtract
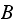 from
from
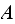 ,
only the term
,
only the term
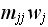 will survive. Hence (5)
becomes
will survive. Hence (5)
becomes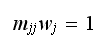 or
or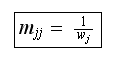 QED.
QED.
If we wait for the chain to arrive at its steady state (i.e. we the chain
probability state vector does not change, or
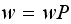 ),
then we observe the chain from that point on, for a long period of time, say
),
then we observe the chain from that point on, for a long period of time, say
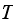 .
The number of times the chain will be in state
.
The number of times the chain will be in state
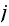 during this time
during this time
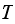 is then given by
is then given by
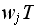 ,
since
,
since
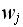 is the probability of the chain being in state
is the probability of the chain being in state
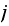 .
So, to find the average number of time units (steps) it took for the chain for
go from state
.
So, to find the average number of time units (steps) it took for the chain for
go from state
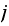 back to state
back to state
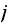 we need to divide
we need to divide
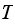 by the number of times the chain was in state
by the number of times the chain was in state
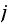 during this time, which we just found as
during this time, which we just found as
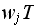
Hence
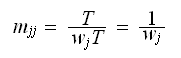
Intuitively this makes sense. Since the smaller the probability that the chain
will be in state
 we would expect the time between the events that the chain is in state
we would expect the time between the events that the chain is in state
 to become larger, So the relation should be an inverse one, as was found. QED
to become larger, So the relation should be an inverse one, as was found. QED