HW problems 8.4 and 8.5, Mathematics 504 CSUF, spring 2008
by Nasser Abbasi
\clearpage

M.C.
is irreducible if there exist no proper closed subset in the state space.
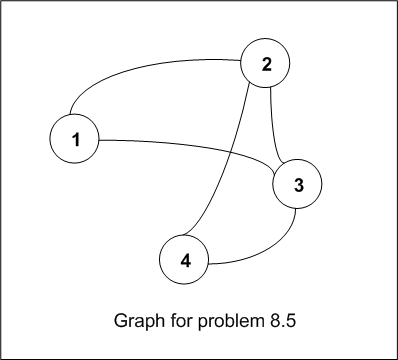
Since we are given that the graph
 is connected, then this means it is possible to visit each vertex from any
other vertex in the graph. But does a connected graph implies no proper closed
subset of the corresponding M.C.? The answer is YES. If we view each vertex as
state, we just need to show that for each edge in
is connected, then this means it is possible to visit each vertex from any
other vertex in the graph. But does a connected graph implies no proper closed
subset of the corresponding M.C.? The answer is YES. If we view each vertex as
state, we just need to show that for each edge in
 between 2 vertices
between 2 vertices
 ,
there corresponds a probability of transition from state
,
there corresponds a probability of transition from state
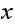 to
to
 which is not zero, and also a probability of transition from state
which is not zero, and also a probability of transition from state
 to
to
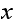 which is also not zero. By showing this, we conclude that the M.C. will switch
(in some number of steps) to any state from any other state, which implies
there is no closed subset, hence
which is also not zero. By showing this, we conclude that the M.C. will switch
(in some number of steps) to any state from any other state, which implies
there is no closed subset, hence
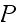 is irreducible.
is irreducible.
But from the definition of
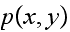 we see that if there is an edge
we see that if there is an edge
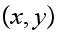 then
then
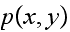 exist and is not zero, and
exist and is not zero, and
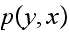 exist and is not zero (since
exist and is not zero (since
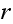 is finite). This completes the proof.
is finite). This completes the proof.
A finite M.C. is regular when, for some integer
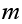 ,
,
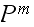 contains only positive elements.
contains only positive elements.
This implies that the one step transition matrix
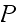 must have at least one entry along the diagonal
must have at least one entry along the diagonal
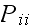 that is none-zero (If all elements along the diagonal are zero, then
that is none-zero (If all elements along the diagonal are zero, then
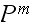 will always contain at least one zero element no matter how large
will always contain at least one zero element no matter how large
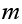 is). But a diagonal element not being zero is the same as saying that at least
one state must be aperiodic (if
is). But a diagonal element not being zero is the same as saying that at least
one state must be aperiodic (if
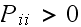 then the period is one).
then the period is one).
To proof that the above chain is regular, we then need to show that at least one state is aperiodic.
Since at most a vertex can have
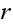 edges, then we can find a vertex
edges, then we can find a vertex
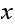 with
with
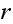 edges connecting it to vertices
edges connecting it to vertices
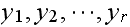 with corresponding one step probability transitions of
with corresponding one step probability transitions of
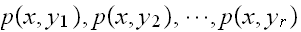 .
(If we can't find such a vertex, the argument will apply to any other vertex,
just replace
.
(If we can't find such a vertex, the argument will apply to any other vertex,
just replace
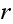 with the number of edges on that vertex and the argument will still apply).
with the number of edges on that vertex and the argument will still apply).
Now let us consider
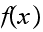 and compare it to each of the
and compare it to each of the
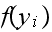 where the
where the
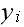 is the vertex with direct edge from
is the vertex with direct edge from
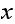 .
There are 2 cases to consider:
.
There are 2 cases to consider:
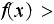 at least one of the
at least one of the
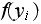 ,
,
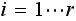
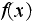
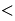 all of
all of
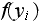 ,
,
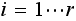
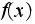
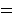 all of
all of
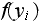 ,
,
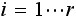
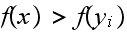 for some
for some
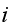 ,
then for this specific
,
then for this specific
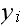 ,
,
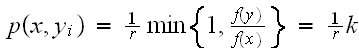 where
where
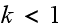 ,
hence
,
hence
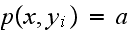 where
where
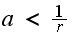 .
Lets assume there was only one
.
Lets assume there was only one
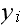 such that the above is true. I.e. at least one of the vertices connected to
such that the above is true. I.e. at least one of the vertices connected to
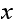 had
had
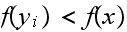 (if more if found, it will not change the argument). Now we add all the
probabilities
(if more if found, it will not change the argument). Now we add all the
probabilities
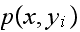 and we found that this sum is
and we found that this sum is
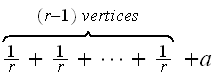 where the
where the
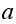 is for that vertex which had
is for that vertex which had
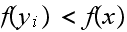 .
Now since
.
Now since
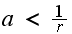 then this sum will be LESS THAN ONE. But the sum of the one step probability
transition from each state must be
then this sum will be LESS THAN ONE. But the sum of the one step probability
transition from each state must be
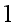 ,
hence to compensate, we must then have
,
hence to compensate, we must then have
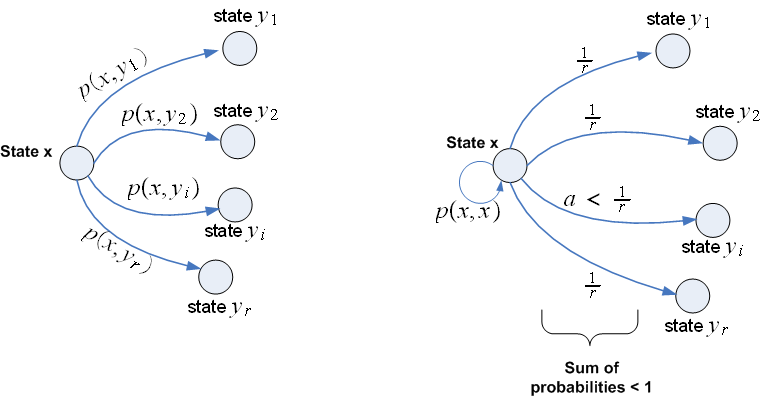
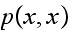 added to make up for the difference. Hence we showed that under case (1) we
can find
added to make up for the difference. Hence we showed that under case (1) we
can find
 which is not zero. This diagram illustrate this
case
which is not zero. This diagram illustrate this
case
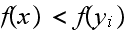 for each
for each
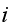 ,
then
,
then
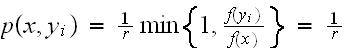 .,
then the sum of the probabilities of transitions from
.,
then the sum of the probabilities of transitions from
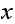 is
is
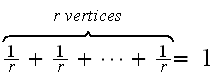 and
we do not need to compensate by adding
and
we do not need to compensate by adding
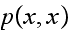 to make up for the deficit. However since now
to make up for the deficit. However since now
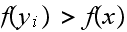 then if we view
then if we view
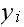 as the
as the
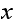 vertex and the
vertex and the
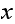 vertex as the
vertex as the
 ,
and consider the probability transitions out of
,
and consider the probability transitions out of
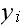 ,
then we are back to case (1) above. Hence in case (2) as well ,we can find a
state in which
,
then we are back to case (1) above. Hence in case (2) as well ,we can find a
state in which
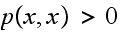 ,
Hence the chain is aperiodic, and since it is irreducible, then it is regular
in this case as well.
,
Hence the chain is aperiodic, and since it is irreducible, then it is regular
in this case as well.
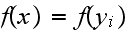 for
for
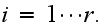 In other words,
In other words,
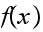 is CONSTANT. In this case
is CONSTANT. In this case
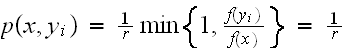
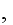 then
the sum of the probabilities of transitions from
then
the sum of the probabilities of transitions from
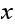 is
is
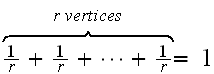 and
we do not need to compensate by adding
and
we do not need to compensate by adding
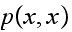 to make up for the deficit. This will be true for any node. Therefore, it is
not possible to find at least one node with the probabilities attached to
edges leaving it is less than one. Hence there are no state with
to make up for the deficit. This will be true for any node. Therefore, it is
not possible to find at least one node with the probabilities attached to
edges leaving it is less than one. Hence there are no state with
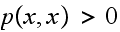 ,
hence in this case, the chain is not aperiodic, and hence the chain is
NOT regular.
,
hence in this case, the chain is not aperiodic, and hence the chain is
NOT regular.
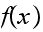 be constant.
be constant.
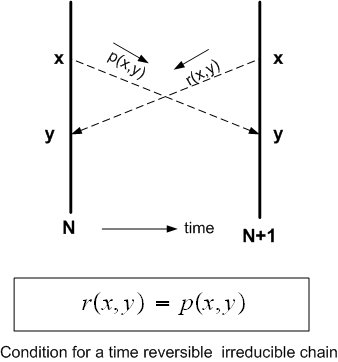
Since the chain is irreducible, then there is a reverse Markov chain (proof is
on page 8.1 and 8.2 of lecture notes). Hence for an irreducible chain the
balance equations hold
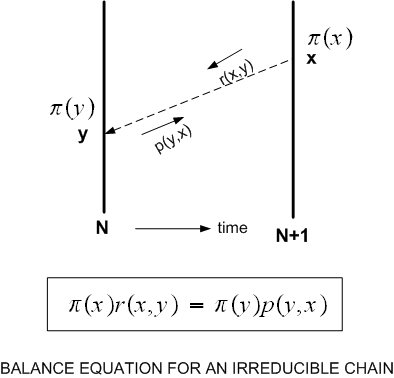
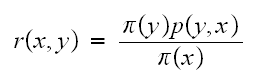 This
diagram helps me remember these formulas
This
diagram helps me remember these formulas
Now if the chain the time reversible as well, then
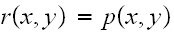 ,
,
Then
the balance equation (1)
becomes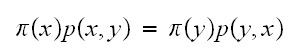 Hence
we need to show that the equation above holds to show the chain is time
reversible.
Hence
we need to show that the equation above holds to show the chain is time
reversible.
Let the LHS of (2) be
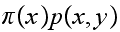 and let RHS of (2) be
and let RHS of (2) be
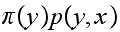 .
Then we will show that LHS=RHS for the following 3 cases:
.
Then we will show that LHS=RHS for the following 3 cases:
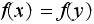
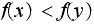
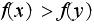
Case(1): Since
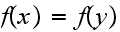 let these be some value, say
let these be some value, say
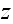
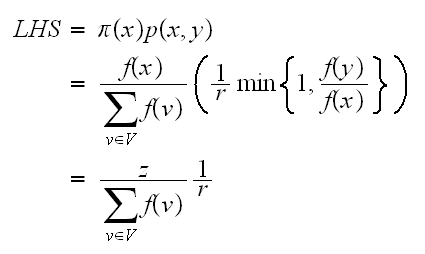 and
and
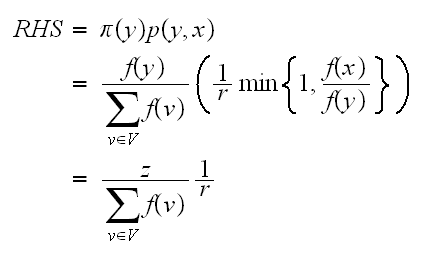 We see that (3) is the same as (4), hence
We see that (3) is the same as (4), hence
case(2):
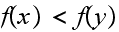
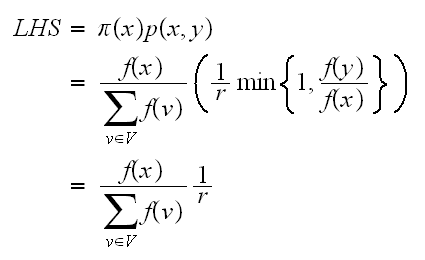 and
and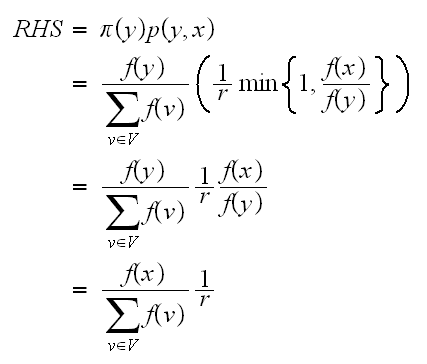 Hence we see that (5) is the same as (6). Hence
Hence we see that (5) is the same as (6). Hence
case
(3):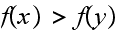
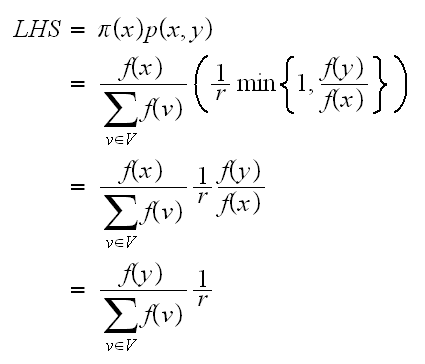 and
and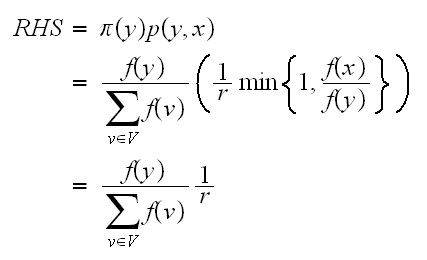 We see that (7) is the same as (8), hence
We see that (7) is the same as (8), hence
The following is the Hastings-Metrpolois algorithm implementation.
This algorithm generates a time-reversible M.C. (referred to as
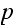 in the lecture notes) given an irreducible M.C. (called
in the lecture notes) given an irreducible M.C. (called
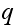 or the original chain) and given a stationary distribution
or the original chain) and given a stationary distribution
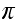 for that chain.
for that chain.

Input:
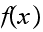 defined over the states
defined over the states
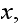 and
and
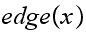 which represents the number of edges connected to
which represents the number of edges connected to
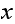
For each state
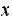 calculate
calculate
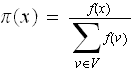 and for each state
and for each state
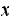 calculate
calculate
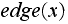
compute
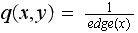 whenever
whenever
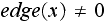 else set
else set
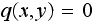
Select a state
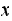 by random to start from.
by random to start from.
Let
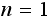 and let
and let
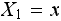
Let
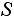 be the set of all states that can be reached in one step from
be the set of all states that can be reached in one step from
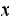 .
These will be the states
.
These will be the states
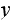 in which
in which
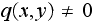
Select a state
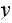 from
from
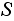 by random (using a uniform
by random (using a uniform
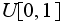 random number generator)
random number generator)
Calculate
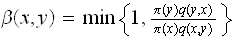
Generate a random number
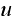 from
from
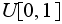
Let
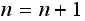
Compare
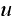 to
to
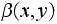 .
.
IF
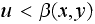 THEN
THEN
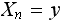 (select the new state) ELSE
(select the new state) ELSE
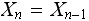 (stay in same state) ENDIF
(stay in same state) ENDIF
Let
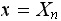
If
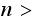 some Max number of iterations or if we reached some convergence limit Then go
to 15
some Max number of iterations or if we reached some convergence limit Then go
to 15
GOTO 5
Algorithm is complete. Now generate the time reversible MC as follows
Scan the state path generate
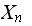 and
count how many times state
and
count how many times state
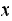 switches to state
switches to state
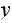 in one step
in one step
Do the above for all the states
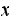
Divide the above number by the total number of steps made to generate
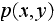
Since the problem now asks to implement
Hastings-Metropolis, then I used the data given at the end of the problem and
implemented the above simulation using that
data Note_2 . Please see
appendix for code and final
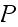 matrix generated.
matrix generated.
This is similar the problem 8.4 part(I). To show that the
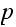 (final M.C.) is irreducible, we need to show that there exist no closed proper
subsets. Since the graph
(final M.C.) is irreducible, we need to show that there exist no closed proper
subsets. Since the graph
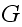 is connected, then we just need to show whenever there is an edge between
vertex
is connected, then we just need to show whenever there is an edge between
vertex
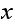 and
and
 then there corresponds in the chain representation of the final
then there corresponds in the chain representation of the final
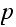 matrix a non-zero
matrix a non-zero
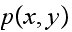 and also a non-zero
and also a non-zero
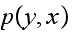 .
This will insure that the each state can transition to each other state, just
as each vertex can be visited from each other vertex (since it is a connected
graph).
.
This will insure that the each state can transition to each other state, just
as each vertex can be visited from each other vertex (since it is a connected
graph).
Let us consider any 2 vertices say
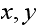 with a direct edge between them (this is the only case we need to consider due
to the argument above). We need to show the resulting
with a direct edge between them (this is the only case we need to consider due
to the argument above). We need to show the resulting
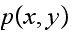 and
and
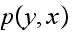 are non-zero
are non-zero
Consider
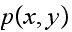 first. Since
first. Since
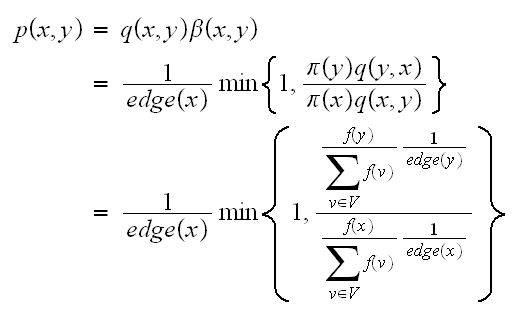 Hence
Hence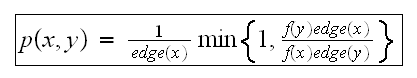 Then it is clear that whenever there is an edge between
Then it is clear that whenever there is an edge between
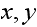 then
then
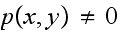 since both
since both
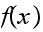 and
and
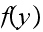 are positive (not zero) and also edge(x) and edge(y) are non-zero as well.
Hence we see that
are positive (not zero) and also edge(x) and edge(y) are non-zero as well.
Hence we see that
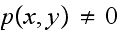 .
Similar argument shows that
.
Similar argument shows that
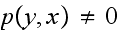 .
.
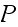 is irreducible
is irreducible
The condition for regular chain
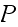 is that there exist at least one state
is that there exist at least one state
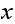 such that
such that
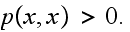 From
(1) above we can decide under what conditions this will occur.
From
(1) above we can decide under what conditions this will occur.
Consider a vertex
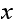 with
with
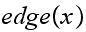 edges from it connected to vertices
edges from it connected to vertices
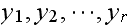 .
Then from (1) we see that
.
Then from (1) we see that
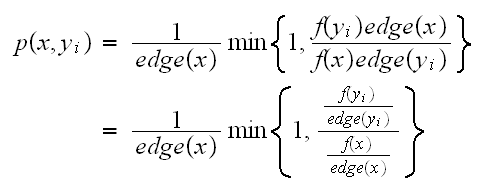 The condition for having
The condition for having
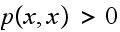 is that
is that
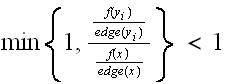 ,
since this will cause
,
since this will cause
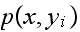 to be some quantity less than
to be some quantity less than
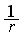 and so when summing over all
and so when summing over all
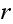 there will be a deficit in the sum and we have to compensate for it to make it
there will be a deficit in the sum and we have to compensate for it to make it
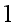 by adding
by adding
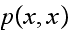 .
But for
.
But for
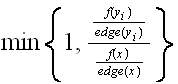 to be less than ONE means that
to be less than ONE means that
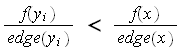
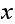 such that the above holds
such that the above holds this vertex is directly connected to. For example, if
this vertex is directly connected to. For example, if
 had the same number of edges from it as does
had the same number of edges from it as does
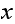 ,
then the condition will be that
,
then the condition will be that
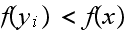 .
And if
.
And if
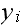 has less or more edges from it than
has less or more edges from it than
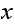 has, then we need the ratio
has, then we need the ratio
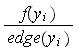 to be less than
to be less than
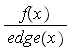 .
.
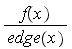 must
be constant for the
must
be constant for the
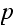 not to be regular
not to be regular
Since the chain is irreducible, then there is a reverse Markov chain (proof is
on page 8.1 and 8.2 of lecture notes). Hence for an irreducible chain the
balance equations hold
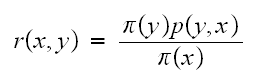 Now if the chain the time reversible as well, then
Now if the chain the time reversible as well, then
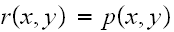 ,
Then the balance equation (1)
becomes
,
Then the balance equation (1)
becomes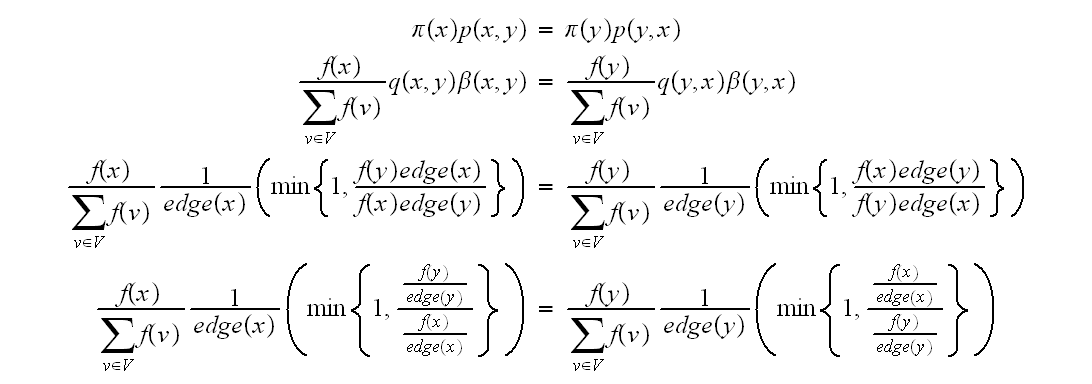
Hence we need to show that the equation (3) above holds to show the chain is time reversible.
There are 3 cases to consider:
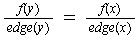
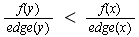
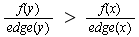
For case (1), LHS of equation (3) simplifies to
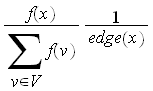 and the RHS of (3) simplifies to
and the RHS of (3) simplifies to
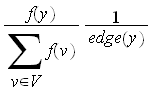 ,
but since
,
but since
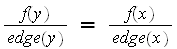 ,
then LHS=RHS.
,
then LHS=RHS.
For case(2), LHS of (3) simplifies
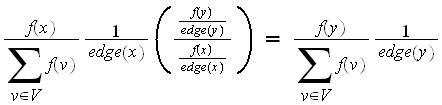 and RHS of (3) simplifies to
and RHS of (3) simplifies to
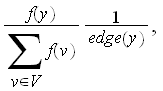 then
LHS=RHS.
then
LHS=RHS.
For case (3), LHS of (3) simplifies
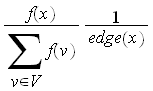 and RHS of (3) simplifies to
and RHS of (3) simplifies to
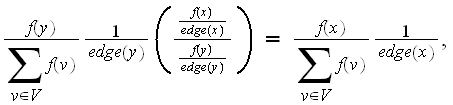 then
LHS=RHS.
then
LHS=RHS.
Hence in all 3 cases we showed the balance equation is satisfied.
A small program written to construct the
 matrix directly following instructions on page 8.4 of lecture notes. The
following is the resulting
matrix directly following instructions on page 8.4 of lecture notes. The
following is the resulting
 matrix
matrix
Now to check that the final chain
 is regular, it was raised to some high power to check that all entries in the
is regular, it was raised to some high power to check that all entries in the
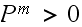 .
This is the result
.
This is the result
The above verifies that the final matrix
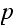 is regular.
is regular.
Using the Hastings-Metropolis simulation algorithm, the convergence to the
above matrix was slow. Had to make 2 million observation to be within 3
decimal points from the above. Here is the
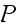 matrix generated from Hastings algorithm for
matrix generated from Hastings algorithm for
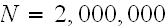
The graph for part(a) and part(b) is the following