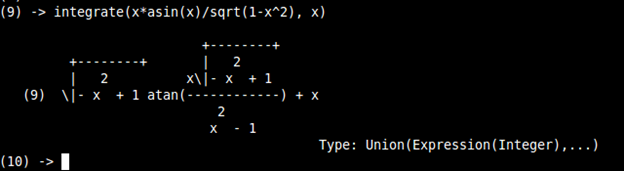
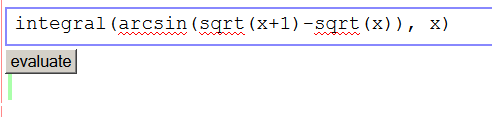
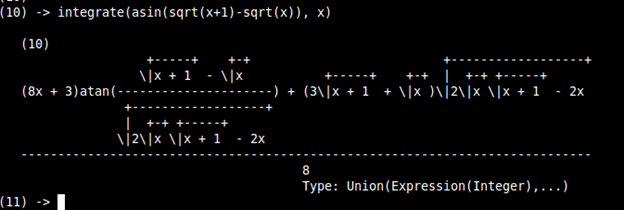
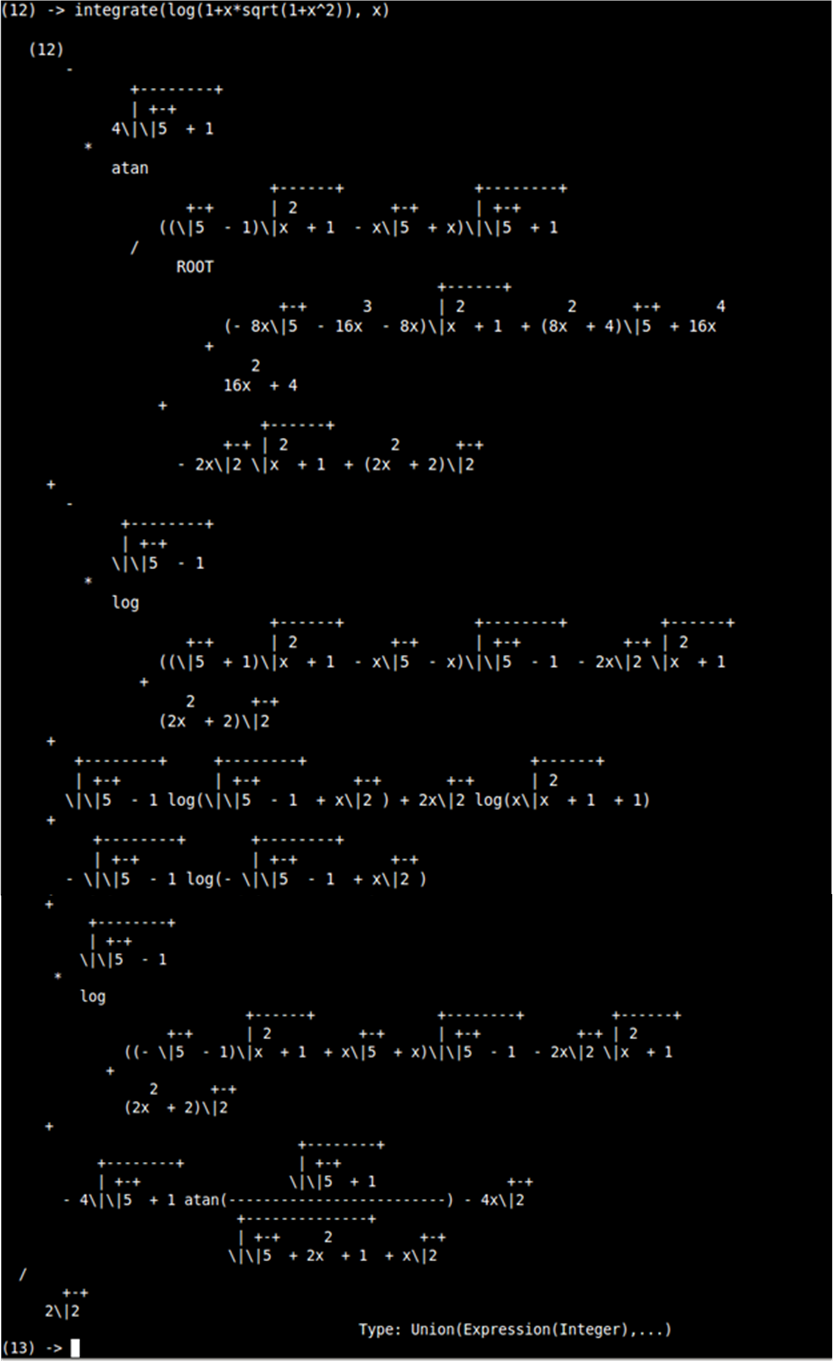
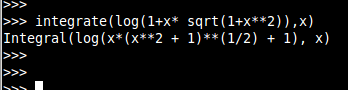
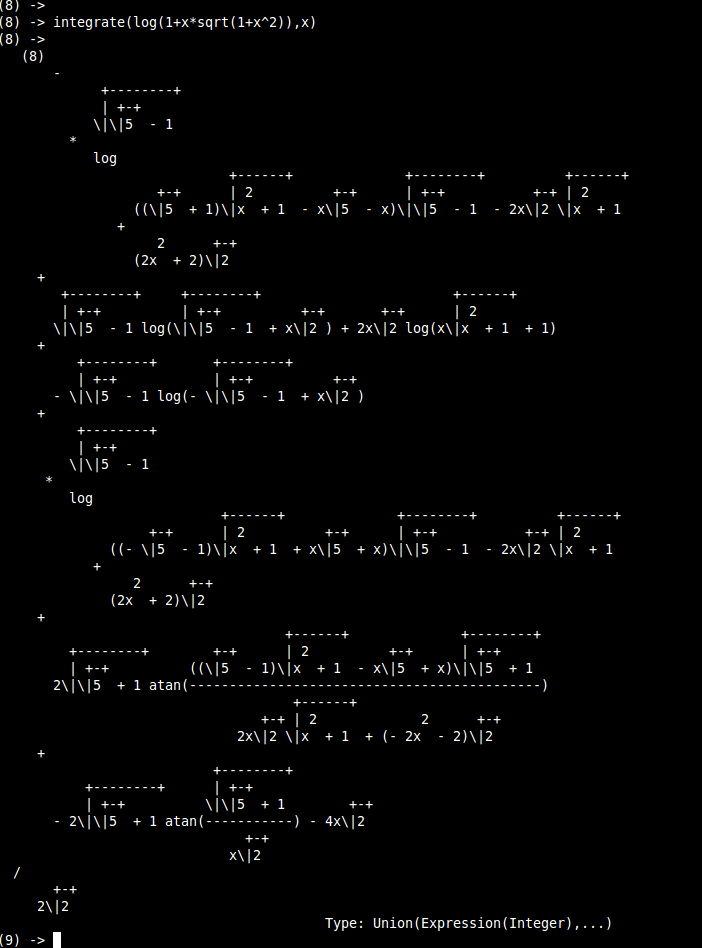
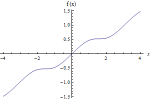
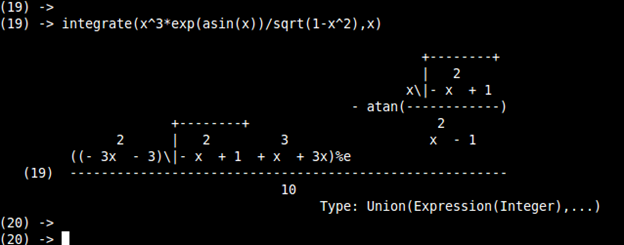
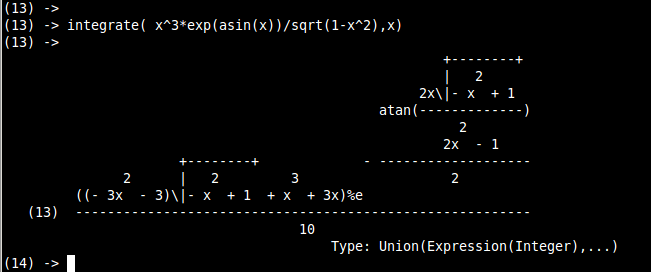
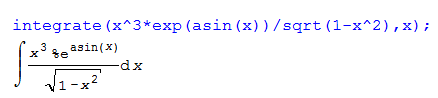
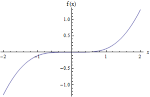
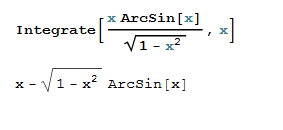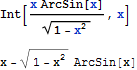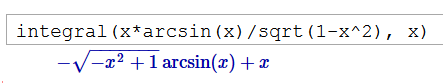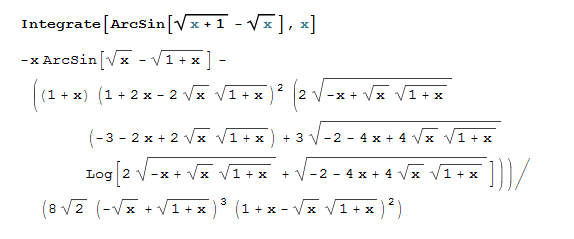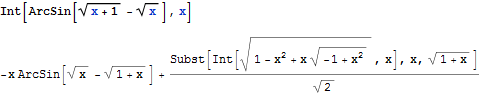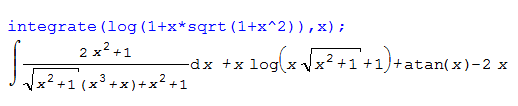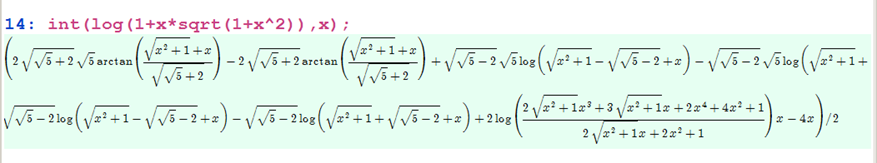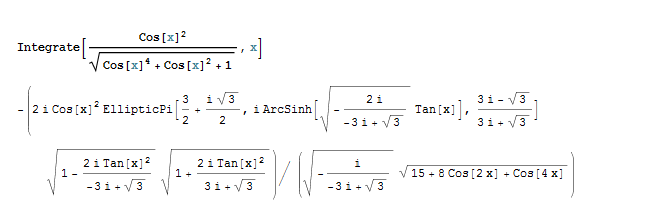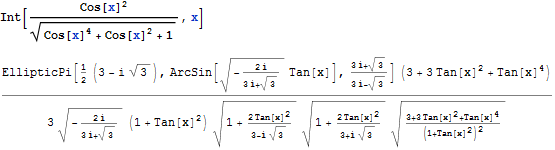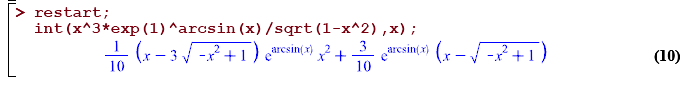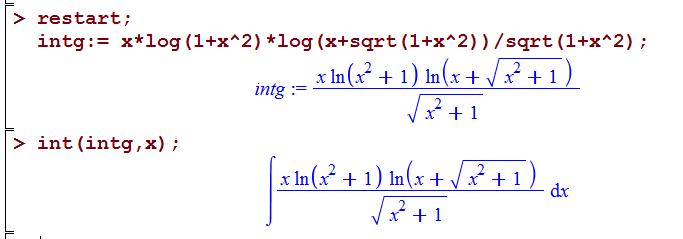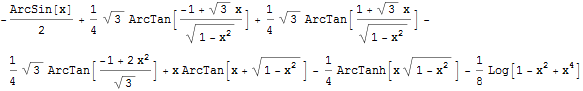|
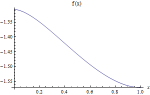
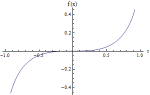
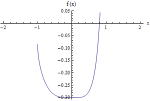
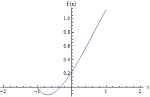
\(-2 \sqrt {1-x^2}+\sqrt {1-x^2} \log (x)+\tanh ^{-1}\left (\sqrt {1-x^2}\right )-x (1-\log (x)) \sin ^{-1}(x)\) |
|
|
M 9.01 |
|
|
Rubi 4.1 |
|
|
Maple 18 |
|
|
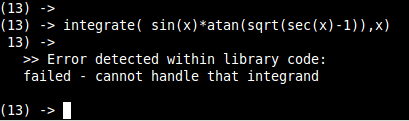
Sage 5.4 |
|
|
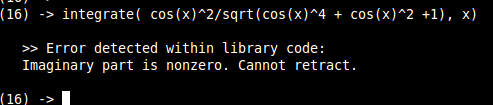
Fricas 1.2 |
|
|
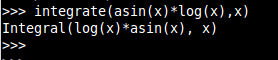
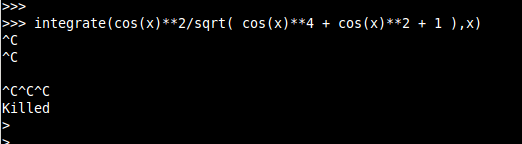
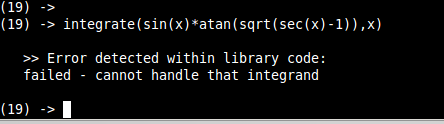
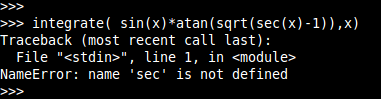
sympy 0.7.1 |
|
|
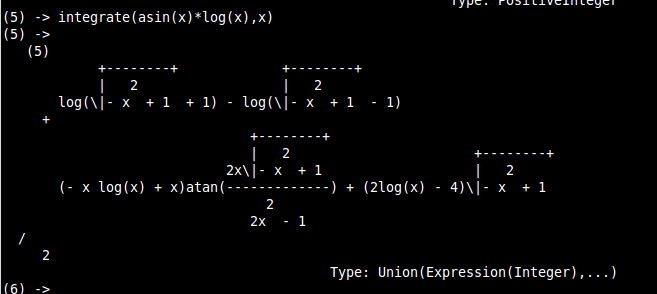
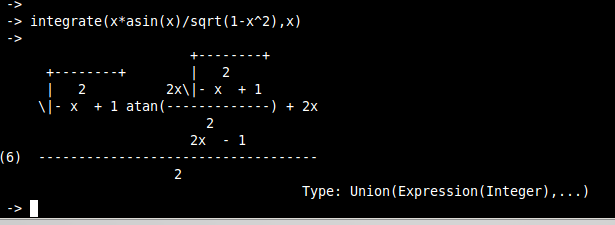
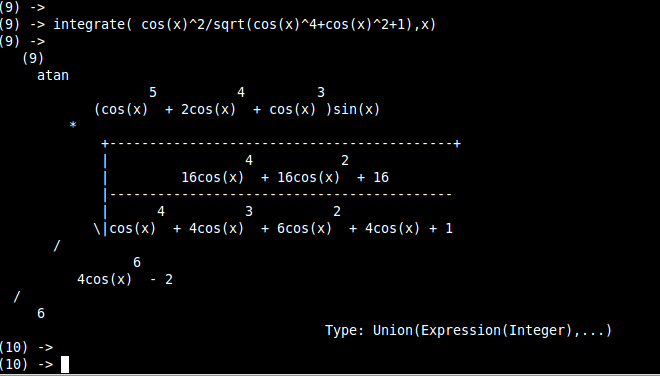
Axiom 5/12 |
|
|
Maxima 5.28.02 |
|
|
reduce 2008 |
|
|
mupad 2013a |
evalin(symengine,'int(asin(x)*log(x),x)') int(asin(x)*log(x), x)
|
|
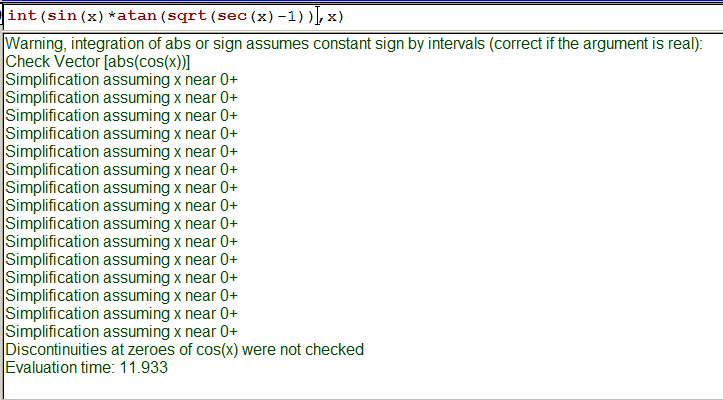
xcas |
|
|
|
|
|
|
|