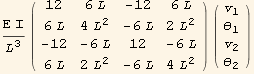
Generating 4-degree of freedom beam stiffness matrix
by Nasser M. Abbasi oct 26,2009
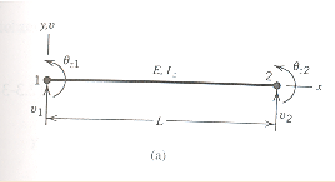
This diagram below is from the book "Concepts and applications of finite element methods" 4th edition. The goal is to find the stiffness matrix for this beam. It has 2 degrees of freedom per node. I will start by assuming the deflection w(x) to be a approximated by a cubic polynomial as a function of x, and then use minimum potential energy approach to find the stiffness matrix.
Assume that the deflection is approximated by 
and from this we need to obtain the shape function N so that we can write 
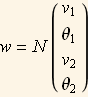hence we see that N must be a 1 by 4 row vector. We call 
the generalized coordinates, and 
as the nodal degrees of freedom.
In[1]:=
Now find an expression for each of the above 4 nodal unknowns in terms of the deflection. Notice that the angle 
as it is being approximated for small deflection (as in the angle of an arc (in radian) is the arc length over radius)
In[6]:=
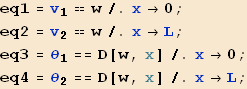
Now to solve for the generalized d.o.f 
In[42]:=
To write the above in the form w = N d we do
In[46]:=
Now that we have found the shape functions, we can find the B matrix. Notice that for beam, the strain matrix B is given by 
In[50]:=
Out[50]=
and now Π, the element potential energy is found (here I only consider strain energy, no loading is needed since we only need to find the element stiffness matrix, not solve a system for unknowns).
In[53]:=
Out[56]=
Out[57]=
Out[58]=
In[59]:=
Out[60]=
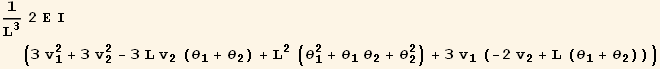
Now that we have the element potential energy, we can generate the element stiffness matrix
In[61]:=
