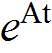
Home
PDF version of this note
Mathematica notebook
Symbolic solution to expansion of natural frequencies method for determining 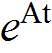
Written by Nasser M. Abbasi, based on lecture given by Professor Barmish, ECE 717, University of Wisconsin, Madison
11/1/2014
The method of finding ![]() using expansion of natural frequencies is first applied to a 2×2 matrix to illustrate the symbolic method. Then a general purpose function is written at the end using the symbolic method and applied to much larger problems for illustrations. This is a standalone function which can be called to determine
using expansion of natural frequencies is first applied to a 2×2 matrix to illustrate the symbolic method. Then a general purpose function is written at the end using the symbolic method and applied to much larger problems for illustrations. This is a standalone function which can be called to determine ![]() for matrices A which can have repeated eigenvalues. The result is verified by comparing the output to Mathematica buildin function MatrixExp[]
for matrices A which can have repeated eigenvalues. The result is verified by comparing the output to Mathematica buildin function MatrixExp[]
Example 1 from lecture done using symbolics
Define A

![]()
Find eigenvalues of A
![]()
Set the eigenvalue multiplers
![]()
Apply ![]() algorithm using expansion of natural frequencies
algorithm using expansion of natural frequencies
![]()
![]()
Automatic generation of lists of unknowns Y(k,i) and list of symbols to b[i] to use for solving Ax=b
![]()
![]()
![]()
Take repeated derivatives of ![]() to generate the set of equations to solve for Y(k,i)
to generate the set of equations to solve for Y(k,i)
![]()
![]()
The problem can be viewed as Ax=b where x=Y(k,i) is the unknowns and b are the symbolic names for the matrix powers.
![]()
![]()
Now solve Ax=b
![]()
![]()
Replace symbols b(i) on the right of the above, by the actual numerical values of the matrix powers
![]()
![]()
Now apply these numerical values to the solution found earlier in order to obtain numerical values for Y(k,i)
![]()
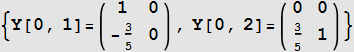
Now since Y(k,i) are now found, evaluate ![]() found above using the above solution
found above using the above solution
![]()
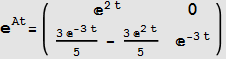
Compare to Mathematica buildin function
![]()
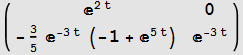
Function to automatically calculate ![]() using symbolic natural frequencies method
using symbolic natural frequencies method

Example 2 from lecture solved using the above function
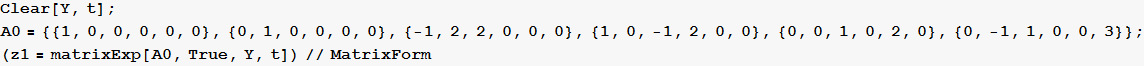
| λ | multiplier |
| 3 | 1 |
| 2 | 3 |
| 1 | 2 |
![]()

![]()
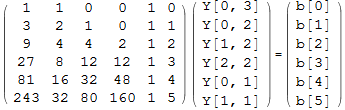
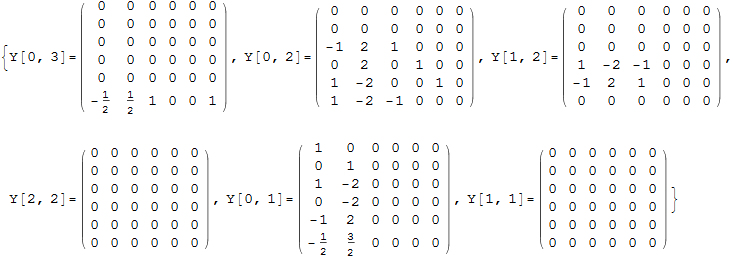
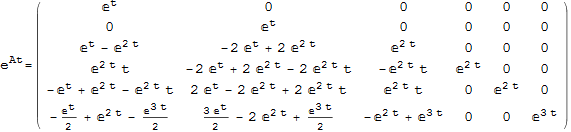
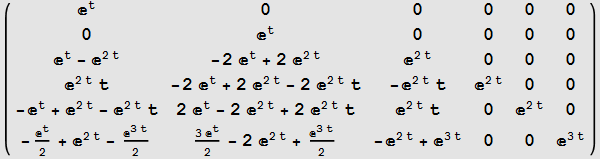
Compare to buildin function to verify
![]()
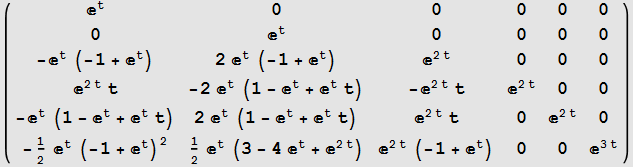
![]()

Verification Method, suggested by Professor Barmish. We Differentiate Matrix ![]() found above and see it is the same as
found above and see it is the same as ![]() for t=0
for t=0

| k | ||
| 0 |  |
 |
| 1 |  |
 |
| 2 |  |
 |
| 3 |  |
 |
| 4 | 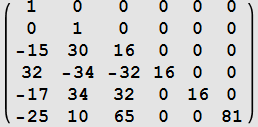 |
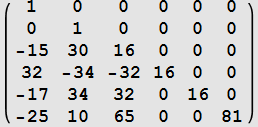 |
| 5 | 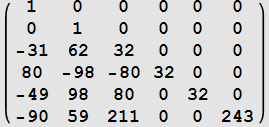 |
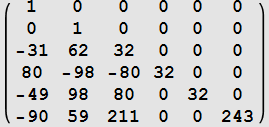 |