
An observation on measurements on A reconstructed from its SVD factorization
by Nasser M. Abbasi, May 20,2007
Starting with a random A matrix, its SVD is found using varying number of its largest singular values k.
Each time, a measure on A is compared with the same measure made on a version of A that was obtained by reconstructing A from its SVD.
For example, A is reconstructed using the first of its singular values, next, using the first 2 of its singular values, next, using the first 3 of its singular values, and so forth until all the singular values are used (the number of the singular value is the rank of A).
Each time the original A matrix is compared with the reconstructed A to obtain a measure of information content in A as a function of k (the number of the singular values used).
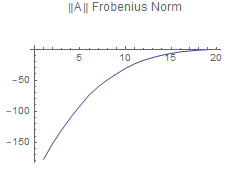
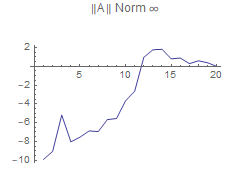
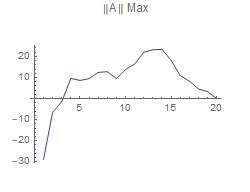
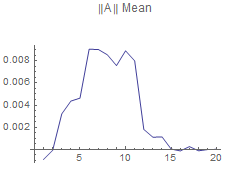
Measures used to compare the original matrix A with the reconstructed A are norm1,norm2,norm infinity,norm Frobenius,max element, and the mean value of A.
This shows that the more singular values used to reconstruct A, the better the approximation will be using any of the measure. However, Using the 2-norm for a measure of A, shows that using any number of singular values will produce as good a reconstruction as the other. So, deciding on which measure to use is important.
Generate a random real matrix 30 by 20

![]()
Determine SVD for matrix A associated with k largest singular values of A. Change k from 1 up to the rank. For Each k, find the norm of the reconstructed A matrix, and compare this norm with the original norm of A. Plot the difference in the norms


Now plot the differences between the largest elements in A and the reconstructed A

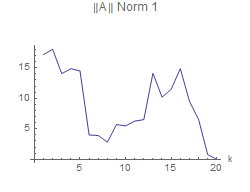 |
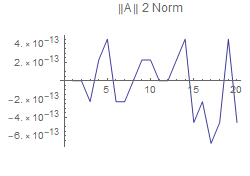 |
 |
 |
 |
 |