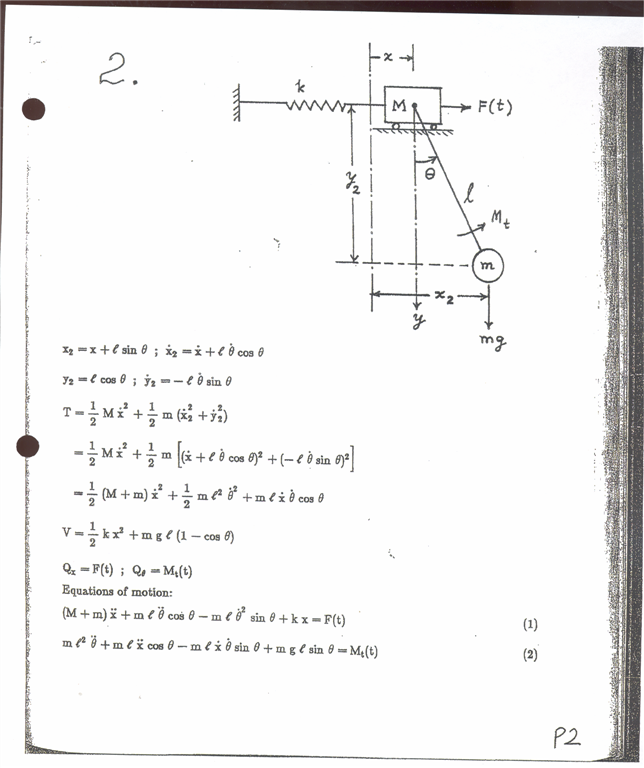
possible error in key solution:

\begin{align*} T & =\frac{1}{2}\left ( M+m\right ) \dot{x}^{2}+\frac{1}{2}mL^{2}\dot{\theta }^{2}+mL\dot{x}\dot{\theta }\cos \theta \\ V & =\frac{1}{2}kx^{2}+mgl\left ( 1-\cos \theta \right ) \end{align*}
Now
\begin{align*} L & =T-V\\ & =\frac{1}{2}\left ( M+m\right ) \dot{x}^{2}+\frac{1}{2}mL^{2}\dot{\theta }^{2}+mL\dot{x}\dot{\theta }\cos \theta -\left ( \frac{1}{2}kx^{2}+mgl\left ( 1-\cos \theta \right ) \right ) \\ & =\frac{1}{2}\left ( M+m\right ) \dot{x}^{2}+\frac{1}{2}mL^{2}\dot{\theta }^{2}+mL\dot{x}\dot{\theta }\cos \theta -\frac{1}{2}kx^{2}-mgl\left ( 1-\cos \theta \right ) \end{align*}
EQM for \(\theta \) show is WRONG. Proof:
\begin{align*} \frac{\partial L}{\partial \dot{\theta }} & =mL^{2}\dot{\theta }+mL\dot{x}\cos \theta \\ \frac{d}{dt}\frac{\partial L}{\partial \dot{\theta }} & =mL^{2}\ddot{\theta }+mL\ddot{x}\cos \theta -mL\dot{x}\dot{\theta }\sin \theta \end{align*}
and
\[ \frac{\partial L}{\partial \theta }=-mL\dot{x}\dot{\theta }\sin \theta -mgl\left ( \sin \theta \right ) \]
Hence, EQM is
\begin{align*} \frac{d}{dt}\frac{\partial L}{\partial \dot{\theta }}-\frac{\partial L}{\partial \theta } & =M_{t}\\ mL^{2}\ddot{\theta }+mL\ddot{x}\cos \theta -mL\dot{x}\dot{\theta }\sin \theta -\left ( -mL\dot{x}\dot{\theta }\sin \theta -mgl\left ( \sin \theta \right ) \right ) & =M_{t}\\ mL^{2}\ddot{\theta }+mL\ddot{x}\cos \theta -mL\dot{x}\dot{\theta }\sin \theta +mL\dot{x}\dot{\theta }\sin \theta +mgl\left ( \sin \theta \right ) & =M_{t}\\ mL^{2}\ddot{\theta }+mL\ddot{x}\cos \theta +mgl\left ( \sin \theta \right ) & =M_{t} \end{align*}
Which is NOT the same as shown in the key solution