

Initially, when mass is given velocity \(v_{0}\) then the equation of motion is\[ m\ddot{x}+k_{2}x=0 \] with IC \(\dot{x}\left ( 0\right ) =v_{0},x\left ( 0\right ) =0\), hence the solution is\[ x\left ( t\right ) =A\cos \omega _{n}t+B\sin \omega _{n}t \] Where \(\omega _{n}=\sqrt{\frac{k_{2}}{m}}\) in this case.
From IC \(x\left ( 0\right ) =0\) we obtain that \(A=0\) and now\[ \dot{x}\left ( t\right ) =B\sqrt{\frac{k_{2}}{m}}\cos \sqrt{\frac{k_{2}}{m}}t \] Hence from IC \(\dot{x}\left ( 0\right ) =v_{0}\) we obtain that \(B=\frac{v_{0}}{\sqrt{\frac{k_{2}}{m}}}\) and then we write the solution as\[ x\left ( t\right ) =\sqrt{\frac{m}{k_{2}}}v_{0}\sin \sqrt{\frac{k_{2}}{m}}t \] The above is the solution for EQM of the mass when it is attached to \(k_{2}\)spring.
Now the mass will move to the right, losing its kinetic energy to the potential energy of the spring until it stops at the maximum displacement on the right, which will be \(\sqrt{\frac{m}{k_{2}}}v_{0}\). Then the mass will starts to move to the left again towards the static equilibrium position, gaining speed as it does and the spring losing potential energy until the mass is back to \(x=0\) where it will have speed of \(v_{0}\) but in the left direction. When it hits the left spring \(k_{1}\), it will move in an EQM given by\[ m\ddot{x}+k_{1}x=0 \] With initial \(x\) given by static equilibrium position (i.e. \(x=0\)) and initial velocity of \(v_{0}\) but to the left direction. Hence as before, we obtain\[ x\left ( t\right ) =\sqrt{\frac{m}{k_{1}}}v_{0}\sin \sqrt{\frac{k_{1}}{m}}t \] The above is the solution for EQM of the mass when it is attached to spring \(k_{1}\). We see that the maximum displacement will be \(x\left ( t\right ) =\sqrt{\frac{m}{k_{1}}}v_{0}\) in this case.
Therefore, we conclude the following:
and
And since \(k_{2}>k_{1}\), then it will move the left a longer distance than to the right.
From above, the period of motion when the mass is attached to \(k_{2}\) is found by setting\(\sqrt{\frac{k_{2}}{m}}t=2\pi ft\) hence \(f=\frac{1}{2\pi }\sqrt{\frac{k_{2}}{m}}\), therefore \(T=2\pi \sqrt{\frac{m}{k_{2}}}\sec \)
The period of motion when the mass is attached to \(k_{1}\) is found by setting\(\sqrt{\frac{k_{1}}{m}}t=2\pi ft\) hence \(f=\frac{1}{2\pi }\sqrt{\frac{k_{1}}{m}}\), therefore \(T=2\pi \sqrt{\frac{m}{k_{1}}}\sec \)
We see that the period when the mass is attached to \(k_{1}\) is longer than the period when the mass is attached to \(k_{2}\).

The Lagrangian which I will call \(\Gamma \) (since I am using \(L\) for the current length of the band) is given by \(T-U\), where \(T\) is the kinetic energy of the system and \(U\) is the potential energy of the system.
We take \(x\) to be from the unstretched length of the rubber band along the length of the band.
First, we determine the velocity of mass \(m\). Assume that the length of the rubber band at any point time is given by \(L\left ( t\right ) \), then\begin{align*} v^{2} & =v_{horizontal}^{2}+v_{vertical}^{2}\\ & =\left [ \frac{d}{dt}\left ( s_{horizontal}\right ) \right ] ^{2}+\left [ \frac{d}{dt}\left ( s_{vertical}\right ) \right ] ^{2}\\ & =\left [ \frac{d}{dt}\left ( L\left ( t\right ) \sin \theta \right ) \right ] ^{2}+\left [ \frac{d}{dt}\left ( L\left ( t\right ) \cos \theta \right ) \right ] ^{2}\\ & =\left [ \dot{L}\left ( t\right ) \sin \theta +L\left ( t\right ) \cos \left ( \theta \right ) \dot{\theta }\right ] ^{2}+\left [ \dot{L}\left ( t\right ) \cos \theta -L\left ( t\right ) \sin \left ( \theta \right ) \dot{\theta }\right ] ^{2}\\ & =\dot{L}^{2}\left ( t\right ) \sin ^{2}\theta +L^{2}\left ( t\right ) \cos ^{2}\left ( \theta \right ) \dot{\theta }^{2}+2\dot{L}\left ( t\right ) \sin \left ( \theta \right ) L\left ( t\right ) \cos \left ( \theta \right ) \dot{\theta }\\ & +\dot{L}^{2}\left ( t\right ) \cos ^{2}\theta +L^{2}\left ( t\right ) \sin ^{2}\left ( \theta \right ) \dot{\theta }^{2}-2\dot{L}\left ( t\right ) \cos \left ( \theta \right ) L\left ( t\right ) \sin \left ( \theta \right ) \dot{\theta }\\ & =\dot{L}^{2}\left ( t\right ) \left [ \sin ^{2}\theta +\cos ^{2}\theta \right ] +L^{2}\left ( t\right ) \dot{\theta }^{2}\left [ \cos ^{2}\left ( \theta \right ) +\sin ^{2}\left ( \theta \right ) \right ] \\ & =\dot{L}^{2}\left ( t\right ) +L^{2}\left ( t\right ) \dot{\theta }^{2} \end{align*}
Therefore, the system kinetic energy is\begin{align*} T & =\frac{1}{2}mv^{2}\\ & =\frac{1}{2}m\left ( \dot{L}^{2}\left ( t\right ) +L^{2}\left ( t\right ) \dot{\theta }^{2}\right ) \end{align*}
Now we find \(U\), the potential energy for the mass, with the help of this diagram
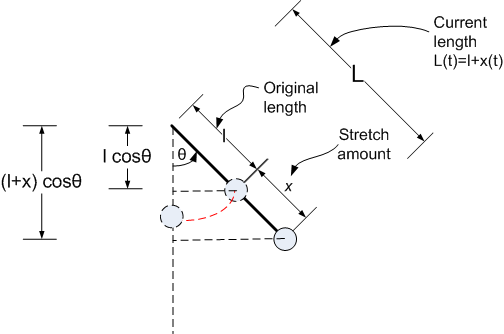
\[ U_{mass}=-mg\left ( L\cos \theta -l\right ) \] Where the minus sign at the front since the mass has lost PE as it is assume \(x\) has stretched the band and hence the mass is lower than its static position.
And the potential energy for the band is\[ U_{band}=\frac{1}{2}kx^{2}\left ( t\right ) \] Hence, the Lagrangian \(\Gamma \) is\begin{align*} \Gamma & =T-U\\ & =\frac{1}{2}m\left ( \dot{L}^{2}\left ( t\right ) +L^{2}\left ( t\right ) \dot{\theta }^{2}\right ) -\left ( \frac{1}{2}kx^{2}\left ( t\right ) -mg\left ( L\cos \theta -l\right ) \right ) \\ & \end{align*}
But \(L=l+x\left ( t\right ) \), hence the above becomes\[ \Gamma =\frac{1}{2}m\left [ \left ( \frac{d}{dt}\left ( l+x\left ( t\right ) \right ) \right ) ^{2}+\left ( l+x\left ( t\right ) \right ) ^{2}\dot{\theta }^{2}\right ] -\left ( \frac{1}{2}kx^{2}\left ( t\right ) -mg\left [ \left ( l+x\left ( t\right ) \right ) \cos \theta -l\right ] \right ) \] Hence\[ \fbox{$\Gamma =\frac{1}{2}m\left [ \dot{x}^{2}\left ( t\right ) +\left ( l^{2}+x^{2}\left ( t\right ) +2lx\left ( t\right ) \right ) \dot{\theta }^{2}\right ] -\frac{1}{2}kx^{2}\left ( t\right ) +mg\left [ l\left ( \cos \theta -1\right ) +x\left ( t\right ) \cos \theta \right ] $}\] Hence EQM is now found. For \(\theta \) we have\begin{align*} \frac{d}{dt}\frac{\partial \Gamma }{\partial \dot{\theta }}-\frac{\partial \Gamma }{\partial \theta } & =0\\ \frac{d}{dt}\left ( \frac{1}{2}m\left [ 2\left ( l^{2}+x^{2}\left ( t\right ) +2lx\left ( t\right ) \right ) \dot{\theta }\right ] \right ) -mg\left [ -l\sin \theta -x\left ( t\right ) \sin \theta \right ] & =0\\ m\left [ \left ( 2x\left ( t\right ) \dot{x}\left ( t\right ) +2l\dot{x}\left ( t\right ) \right ) \dot{\theta }+\left ( l^{2}+x^{2}\left ( t\right ) +2lx\left ( t\right ) \right ) \ddot{\theta }\right ] +mg\left [ l\sin \theta +x\left ( t\right ) \sin \theta \right ] & =0\\ \left ( l^{2}+x^{2}\left ( t\right ) +2lx\left ( t\right ) \right ) \ddot{\theta }+\left ( 2x\left ( t\right ) \dot{x}\left ( t\right ) +2l\dot{x}\left ( t\right ) \right ) \dot{\theta }+g\sin \theta \left [ l+x\left ( t\right ) \right ] & =0\\ \left ( l^{2}+x^{2}\left ( t\right ) +2lx\left ( t\right ) \right ) \ddot{\theta }+\left ( l+x\left ( t\right ) \right ) 2\dot{x}\left ( t\right ) \dot{\theta }+g\sin \theta \left [ l+x\left ( t\right ) \right ] & =0 \end{align*}
The above can be simplified more if we observer that \(\left ( l^{2}+x^{2}\left ( t\right ) +2lx\left ( t\right ) \right ) =\left [ l+x\left ( t\right ) \right ] ^{2}=L^{2}\) and \(l+x\left ( t\right ) =L\), hence EQM becomes\[ L^{2}\ddot{\theta }+2L\dot{x}\dot{\theta }+gL\sin \theta =0 \] Or\[ \fbox{$L\ddot{\theta }+2\dot{x}\dot{\theta }+g\sin \theta =0$}\] Using small angle approximation, \(\sin \theta \simeq \theta \) and \(\dot{\theta }\) can be neglected, we obtain\begin{align*} L\ddot{\theta }+g\theta & =0\\ \ddot{\theta }+\frac{g}{L}\theta & =0 \end{align*}
Hence, the effective stiffness is \(\frac{g}{L}\) and \(\omega _{n_{\theta }}=\sqrt{\frac{g}{L}}=\sqrt{\frac{g}{l+x\left ( t\right ) }}\)Hence we observe that as the band is stretched more, \(\omega _{n}\) becomes smaller and the period becomes longer. Now we derive the EQM in the \(x\) direction
\(\frac{1}{2}m\left [ \dot{x}^{2}\left ( t\right ) +\left ( l^{2}+x^{2}\left ( t\right ) +2lx\left ( t\right ) \right ) \dot{\theta }^{2}\right ] -\frac{1}{2}kx^{2}\left ( t\right ) +mg\left [ l\left ( \cos \theta -1\right ) +x\left ( t\right ) \cos \theta \right ] \) \begin{align*} \frac{d}{dt}\frac{\partial \Gamma }{\partial \dot{x}}-\frac{\partial \Gamma }{\partial x} & =0\\ \frac{d}{dt}\left ( m\dot{x}\left ( t\right ) \right ) +kx\left ( t\right ) & =0 \end{align*}
Hence EQM is \[ \fbox{$\ddot{x}\left ( t\right ) +\frac{k}{m}x\left ( t\right ) =0$}\] Hence, the effective stiffness is \(\frac{k}{m}\) and \(\omega _{n_{x}}=\sqrt{\frac{k}{m}}\) The solutions can now be given easily as\begin{align*} \theta \left ( t\right ) & =A\cos \omega _{n_{\theta }}t+B\sin \omega _{n_{\theta }}t\\ x\left ( t\right ) & =C\cos \omega _{n_{x}}t+D\sin \omega _{n_{x}}t \end{align*}
or\begin{align*} \theta \left ( t\right ) & =A\cos \sqrt{\frac{g}{l+x\left ( t\right ) }}t+B\sin \sqrt{\frac{g}{l+x\left ( t\right ) }}t\\ L\left ( t\right ) & =l+C\cos \sqrt{\frac{k}{m}}t+D\sin \sqrt{\frac{k}{m}}t \end{align*}
Where \(A,B,C,D\) can be obtained from initial conditions.
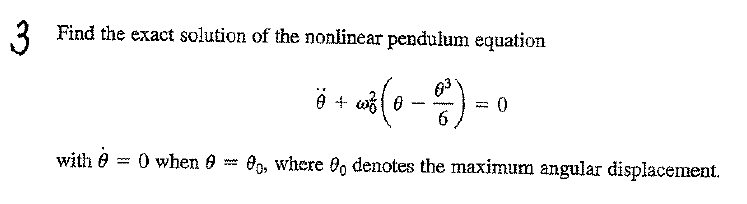
EQM is given by\[ \ddot{\theta }+\omega _{0}^{2}\left ( \theta -\frac{\theta ^{3}}{6}\right ) =0 \] The above can be put in the form \begin{equation} \ddot{\theta }=f\left ( \theta \right ) \tag{1} \end{equation} Where \[ f\left ( \theta \right ) =\omega _{0}^{2}\left ( \frac{\theta ^{3}}{6}-\theta \right ) \] Hence, this is an autonomous differential equation since \(f\left ( \theta \right ) \) does not depend on the independent variable \(t\) explicitly.
Now, Let \(x_{1}=\theta \) and \(x_{2}=\dot{\theta }\), then \(\frac{dx_{1}}{dt}=x_{2}\) and using the new state variables we can rewrite the differential equation as\begin{align*} \frac{dx_{2}}{dt}+\omega _{0}^{2}\left ( x_{1}-\frac{x_{1}^{3}}{6}\right ) & =0\\ \frac{dx_{2}}{dx_{1}}\frac{dx_{1}}{dt} & =-\omega _{0}^{2}\left ( x_{1}-\frac{x_{1}^{3}}{6}\right ) \\ \frac{dx_{2}}{dx_{1}}x_{2} & =-\omega _{0}^{2}\left ( x_{1}-\frac{x_{1}^{3}}{6}\right ) \\ x_{2}dx_{2} & =-\omega _{0}^{2}\left ( x_{1}-\frac{x_{1}^{3}}{6}\right ) dx_{1} \end{align*}
Integrate both side\begin{align*} \frac{x_{2}^{2}}{2} & =-\omega _{0}^{2}\int \left ( x_{1}-\frac{x_{1}^{3}}{6}\right ) dx_{1}+C_{1}\\ x_{2}^{2} & =-2\omega _{0}^{2}\left [ \frac{x_{1}^{2}}{2}-\frac{x_{1}^{4}}{24}\right ] +C_{1} \end{align*}
But \(x_{2}=\dot{\theta }\) and \(x_{1}=\theta \), then the above becomes\begin{equation} \dot{\theta }^{2}=-2\omega _{0}^{2}\left [ \frac{\theta ^{2}}{2}-\frac{\theta ^{4}}{24}\right ] +C_{1} \tag{2} \end{equation} We are told that when \(\theta =\theta _{0}\) then \(\dot{\theta }=0\), hence from the above\begin{align*} 0 & =-2\omega _{0}^{2}\left [ \frac{\theta _{0}^{2}}{2}-\frac{\theta _{0}^{4}}{24}\right ] +C_{1}\\ C_{1} & =\omega _{0}^{2}\left [ \theta _{0}^{2}-\frac{\theta _{0}^{4}}{12}\right ] \end{align*}
Then (2) becomes\[ \dot{\theta }^{2}=-2\omega _{0}^{2}\left [ \frac{\theta ^{2}}{2}-\frac{\theta ^{4}}{24}\right ] +\omega _{0}^{2}\left [ \theta _{0}^{2}-\frac{\theta _{0}^{4}}{12}\right ] \] or\[ \dot{\theta }^{2}=\omega _{0}^{2}\left [ \frac{1}{12}\theta ^{4}-\theta ^{2}\right ] +\omega _{0}^{2}\left [ \theta _{0}^{2}-\frac{\theta _{0}^{4}}{12}\right ] \] Therefore\begin{align*} \dot{\theta } & =\omega _{0}\sqrt{\frac{1}{12}\theta ^{4}-\theta ^{2}+\theta _{0}^{2}-\frac{\theta _{0}^{4}}{12}}\\ \frac{d\theta }{dt} & =\frac{\omega _{0}}{\sqrt{12}}\sqrt{\theta ^{4}-12\theta ^{2}+12\theta _{0}^{2}-\theta _{0}^{4}}\\ & =\frac{\omega _{0}}{2\sqrt{3}}\sqrt{\theta ^{2}\left ( \theta ^{2}-12\right ) +\theta _{0}^{2}\left ( 12-\theta _{0}^{2}\right ) } \end{align*}
Hence integrating the above we obtain\begin{align*} \int \frac{1}{\sqrt{\theta ^{2}\left ( \theta ^{2}-12\right ) +\theta _{0}^{2}\left ( 12-\theta _{0}^{2}\right ) }}d\theta & =\frac{\omega _{0}}{2\sqrt{3}}\int dt+C_{2}\\ \int \frac{1}{\sqrt{\theta ^{2}\left ( \theta ^{2}-12\right ) +\theta _{0}^{2}\left ( 12-\theta _{0}^{2}\right ) }}d\theta & =\frac{\omega _{0}}{2\sqrt{3}}t+C_{2} \end{align*}
We can stop here. What remains is to evaluate the integral above by some analytical method to obtain an expression for \(\theta \left ( t\right ) \). The constant \(C_{2}\) can be found if we are given the position initial condition.
EQM is given by
\[ \ddot{\theta }+\omega _{0}^{2}\left ( \theta -\frac{\theta ^{3}}{6}\right ) =0 \]
The above can be put in the form \begin{equation} \ddot{\theta }=f\left ( \theta \right ) \tag{1} \end{equation}
Where \[ f\left ( \theta \right ) =\omega _{0}^{2}\left ( \frac{\theta ^{3}}{6}-\theta \right ) \]
Hence, this is an autonomouse differential equation since \(f\left ( \theta \right ) \) does not depend on the independent variable \(t\) explicility.
To solve (1), we first write
\begin{align} \ddot{\theta } & =\frac{d}{dt}\left ( \frac{d\theta }{dt}\right ) \nonumber \\ & =\left [ \frac{d}{d\theta }\left ( \frac{d\theta }{dt}\right ) \right ] \frac{d\theta }{dt}\nonumber \\ & =\left [ \frac{d}{d\theta }\left ( \left ( \frac{dt}{d\theta }\right ) ^{-1}\right ) \right ] \left ( \frac{dt}{d\theta }\right ) ^{-1} \tag{2} \end{align}
But \[ \frac{d}{d\theta }\left ( \left ( \frac{dt}{d\theta }\right ) ^{-1}\right ) =-\left ( \frac{dt}{d\theta }\right ) ^{-2}\frac{d^{2}t}{d\theta ^{2}}\left ( \frac{dt}{d\theta }\right ) ^{-1}\]
Substitute the above into (2) we obtain
\begin{align} \ddot{\theta } & =-\left ( \frac{dt}{d\theta }\right ) ^{-2}\frac{d^{2}t}{d\theta ^{2}}\left ( \frac{dt}{d\theta }\right ) ^{-1}\nonumber \\ & =-\left ( \frac{dt}{d\theta }\right ) ^{-3}\frac{d^{2}t}{d\theta ^{2}} \tag{3} \end{align}
But \begin{equation} \frac{1}{2}\frac{d}{d\theta }\left ( \left ( \frac{dt}{d\theta }\right ) ^{-2}\right ) =-\left ( \frac{dt}{d\theta }\right ) ^{-3}\frac{d^{2}t}{d\theta ^{2}} \tag{4} \end{equation}
Compare (4) and (3) we see that (3) can be written as
\[ \ddot{\theta }=\frac{1}{2}\frac{d}{d\theta }\left ( \left ( \frac{dt}{d\theta }\right ) ^{-2}\right ) \]
THerefore, we use this expression for \(\ddot{\theta }\) in (1) and obtain
\[ \frac{1}{2}\frac{d}{d\theta }\left ( \left ( \frac{dt}{d\theta }\right ) ^{-2}\right ) =f\left ( \theta \right ) \]
Substitute the expression for \(f\left ( \theta \right ) \) we obtain
\[ \fbox{$\frac{1}{2}\frac{d}{d\theta }\left ( \left ( \frac{dt}{d\theta }\right ) ^{-2}\right ) =\omega _{0}^{2}\left ( \frac{\theta ^{3}}{6}-\theta \right ) $}\]
Integrate we obtain
\begin{align*} \frac{1}{2}\left ( \frac{dt}{d\theta }\right ) ^{-2} & =\int \omega _{0}^{2}\left ( \frac{\theta ^{3}}{6}-\theta \right ) d\theta +C_{1}\\ \left ( \frac{dt}{d\theta }\right ) ^{2} & =\frac{1}{2\int \omega _{0}^{2}\left ( \frac{\theta ^{3}}{6}-\theta \right ) d\theta +C_{1}}\\ & =\frac{1}{2\omega _{0}^{2}\left ( \frac{\theta ^{4}}{4\times 6}-\frac{\theta ^{2}}{2}\right ) +C_{1}} \end{align*}
Hence
\[ \frac{dt}{d\theta }=\frac{1}{\sqrt{2\omega _{0}^{2}\left ( \frac{\theta ^{4}}{4\times 6}-\frac{\theta ^{2}}{2}\right ) +C_{1}}}\]
Integrate again, we obtain
\begin{align*} t & =\int \left ( 2\omega _{0}^{2}\left ( \frac{\theta ^{4}}{24}-\frac{\theta ^{2}}{2}\right ) +C_{1}\right ) ^{\frac{-1}{2}}d\theta +C_{2}\\ & =C_{2}+\int \frac{1}{\sqrt{2\omega _{0}^{2}\left ( \frac{\theta ^{4}}{24}-\frac{\theta ^{2}}{2}\right ) +C_{1}}}d\theta \\ & =C_{2}+\int \frac{1}{\sqrt{\frac{\theta ^{4}}{12}-\omega _{0}^{2}\theta ^{2}+C_{1}}}d\theta \\ & =C_{2}+\int \frac{\sqrt{12}}{\sqrt{\theta ^{4}-12\omega _{0}^{2}\theta ^{2}+C_{3}}}d\theta \end{align*}
Where \(C_{3}=12C_{1}\), a new constant. Hence
\[ \fbox{$t=C_{2}+2\sqrt{3}\int \frac{1}{\sqrt{\theta ^{4}-12\omega _{0}^{2}\theta ^{2}+C_{3}}}d\theta $}\]
second approach
Let \(\left . \begin{array} [c]{c}x_{1}=\theta \\ x_{2}=\dot{\theta }\end{array} \right \} \begin{array} [c]{l}\dot{x}_{1}=x_{2}\\ \dot{x}_{2}=-\omega _{0}^{2}\left ( x_{1}-\frac{x_{1}^{3}}{6}\right ) \end{array} \), hence using the new state variables we can rewrite the differential equation as
\begin{align*} \ddot{\theta }+\omega _{0}^{2}\left ( \theta -\frac{\theta ^{3}}{6}\right ) & =0\\ \frac{dx_{2}}{dt}+\omega _{0}^{2}\left ( x_{1}-\frac{x_{1}^{3}}{6}\right ) & =0\\ \frac{dx_{2}}{dx_{1}}\frac{dx_{1}}{dt} & =-\omega _{0}^{2}\left ( x_{1}-\frac{x_{1}^{3}}{6}\right ) \\ \frac{dx_{2}}{dx_{1}}x_{2} & =-\omega _{0}^{2}\left ( x_{1}-\frac{x_{1}^{3}}{6}\right ) \\ x_{2}dx_{2} & =-\omega _{0}^{2}\left ( x_{1}-\frac{x_{1}^{3}}{6}\right ) dx_{1} \end{align*}
Integrate both side
\begin{align*} \frac{x_{2}^{2}}{2} & =-\omega _{0}^{2}\int \left ( x_{1}-\frac{x_{1}^{3}}{6}\right ) dx_{1}+C_{1}\\ x_{2}^{2} & =-2\omega _{0}^{2}\left [ \frac{x_{1}^{2}}{2}-\frac{x_{1}^{4}}{24}\right ] +C_{1} \end{align*}
But \(x_{2}=\dot{\theta }\) and \(x_{1}=\theta \), then the above becomes
\begin{equation} \dot{\theta }^{2}=-2\omega _{0}^{2}\left [ \frac{\theta ^{2}}{2}-\frac{\theta ^{4}}{24}\right ] +C_{1}\tag{2} \end{equation}
We are told that when \(\theta =\theta _{0}\) then \(\dot{\theta }=0\), hence from the above
\begin{align*} 0 & =-2\omega _{0}^{2}\left [ \frac{\theta _{0}^{2}}{2}-\frac{\theta _{0}^{4}}{24}\right ] +C_{1}\\ C_{1} & =\omega _{0}^{2}\left [ \theta _{0}^{2}-\frac{\theta _{0}^{4}}{12}\right ] \end{align*}
Then (2) becomes
\[ \dot{\theta }^{2}=-2\omega _{0}^{2}\left [ \frac{\theta ^{2}}{2}-\frac{\theta ^{4}}{24}\right ] +\omega _{0}^{2}\left [ \theta _{0}^{2}-\frac{\theta _{0}^{4}}{12}\right ] \]
or
\begin{align*} \dot{\theta }^{2} & =-\omega _{0}^{2}\left [ \theta ^{2}-\frac{1}{12}\theta ^{4}\right ] +\omega _{0}^{2}\left [ \theta _{0}^{2}-\frac{\theta _{0}^{4}}{12}\right ] \\ \dot{\theta } & =\sqrt{\omega _{0}^{2}\left [ \frac{1}{12}\theta ^{4}-\theta ^{2}\right ] +\omega _{0}^{2}\left [ \theta _{0}^{2}-\frac{\theta _{0}^{4}}{12}\right ] }\\ & =\omega _{0}\sqrt{\frac{1}{12}\theta ^{4}-\theta ^{2}+\theta _{0}^{2}-\frac{\theta _{0}^{4}}{12}}\\ & =\frac{\omega _{0}}{2\sqrt{3}}\sqrt{\theta ^{4}-12\theta ^{2}+12\theta _{0}^{2}-\theta _{0}^{4}} \end{align*}
Hence integrating the above we obtain
\begin{align*} \theta \left ( t\right ) & =\frac{\omega _{0}}{2\sqrt{3}}\int \sqrt{\theta ^{4}-12\theta ^{2}+12\theta _{0}^{2}-\theta _{0}^{4}}dt\\ & =\left ( \frac{\omega _{0}}{2\sqrt{3}}\sqrt{\theta ^{4}-12\theta ^{2}+12\theta _{0}^{2}-\theta _{0}^{4}}\right ) t+C_{2} \end{align*}
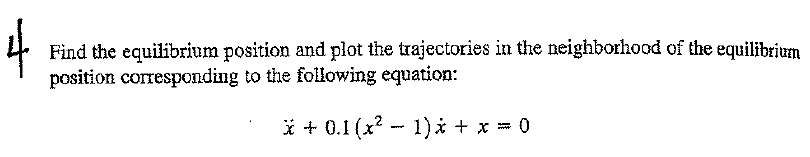
The nonlinear equation is\[ \ddot{x}+0.1\left ( x^{2}-1\right ) \dot{x}+x=0 \] Let\[ \left . \begin{array} [c]{c}x_{1}=x\\ x_{2}=\dot{x}\end{array} \right \} \left . \begin{array} [c]{l}\dot{x}_{1}=\dot{x}\\ \dot{x}_{2}=-0.1\left ( x^{2}-1\right ) \dot{x}-x \end{array} \right \} \begin{array} [c]{l}\dot{x}_{1}=x_{2}\\ \dot{x}_{2}=-0.1\left ( x_{1}^{2}-1\right ) x_{2}-x_{1}\end{array} \] Hence\[\begin{pmatrix} \dot{x}_{1}\\ \dot{x}_{2}\end{pmatrix} =\begin{pmatrix} x_{2}\\ -0.1\left ( x_{1}^{2}-1\right ) x_{2}-x_{1}\end{pmatrix} =\begin{pmatrix} g\left ( x_{1},x_{2}\right ) \\ f\left ( x_{1},x_{2}\right ) \end{pmatrix} \] Solve for \(\begin{pmatrix} \dot{x}_{1}\\ \dot{x}_{2}\end{pmatrix} =\begin{pmatrix} 0\\ 0 \end{pmatrix} \) for equilibrium. Hence \(x_{2}=0\) and therefore \(x_{1}=0\) as well. Now we obtain the linearized state matrix \(A\) at the equilibrium point found. First we note that \(\frac{\partial g}{\partial x_{1}}=0,\frac{\partial g}{\partial x_{2}}=1,\frac{\partial f}{\partial x_{1}}=\frac{\partial }{\partial x_{1}}\left ( -0.1x_{1}^{2}x_{2}+0.1x_{2}-x_{1}\right ) =-0.2x_{1}x_{2}-1\) and \(\frac{\partial f}{\partial x_{2}}=-0.1x_{1}^{2}+0.1\), hence
\begin{align*} A & =\begin{pmatrix} \frac{\partial g}{\partial x_{1}} & \frac{\partial g}{\partial x_{2}}\\ \frac{\partial f}{\partial x_{1}} & \frac{\partial f}{\partial x_{2}}\end{pmatrix} _{x_{1}=0,x_{2}=0}\\ & =\begin{pmatrix} 0 & 1\\ -0.2x_{1}x_{2}-1 & -0.1x_{1}^{2}+0.1 \end{pmatrix} _{x_{1}=0,x_{2}=0}\\ & =\begin{pmatrix} 0 & 1\\ -1 & 0.1 \end{pmatrix} \end{align*}
Find the eigenvalues, we obtain\begin{align*} \begin{vmatrix} -\lambda & 1\\ -1 & 0.1-\lambda \end{vmatrix} & =0\\ -0.1\lambda +\lambda ^{2}+1 & =0 \end{align*}
Hence \[ \lambda _{1,2}=\left \{ 0.05+0.998\,75\allowbreak i,0.05-0.998\,75\allowbreak i\right \} \] This is of the form \[ \lambda =\alpha \pm \beta i \] With \(\alpha >0\), hence unstable, and spiral out. So. now we can draw the phase portrait near \(\left ( 0,0\right ) \) as shown below.
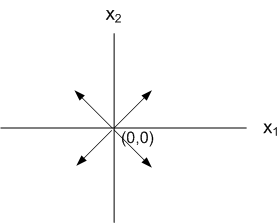
Side QUESTION:
If I wanted to draw the phase plot itself, I am getting this. How to finish this last step? It is not separable?
To obtain phase plane plot, we need to express \(x_{2}\) as function of \(x_{1}\). Looking at the original nonlinear differential equation again and rewrite using the state variables, we obtain\begin{align*} \ddot{x}+0.1\left ( x^{2}-1\right ) \dot{x}+x & =0\\ \frac{dx_{2}}{dt}+0.1\left ( x_{1}^{2}-1\right ) x_{2}+x_{1} & =0\\ \frac{dx_{2}}{dx_{1}}\frac{dx_{1}}{dt}+0.1\left ( x_{1}^{2}-1\right ) x_{2}+x_{1} & =0\\ \frac{dx_{2}}{dx_{1}}x_{2}+0.1\left ( x_{1}^{2}-1\right ) x_{2}+x_{1} & =0\\ \frac{dx_{2}}{dx_{1}}x_{2}+0.1x_{1}^{2}x_{2}-0.1x_{2}+x_{1} & =0\\ \frac{dx_{2}}{dx_{1}} & =0.1-0.1x_{1}^{2}-\frac{x_{1}}{x_{2}} \end{align*}
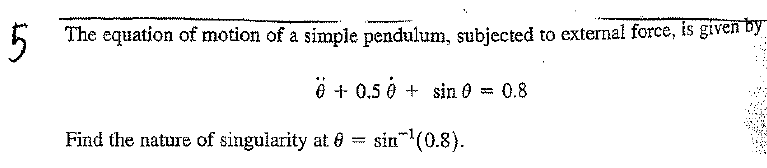
The equation is \[ \ddot{\theta }+0.5\dot{\theta }+\sin \theta =0.8 \] Let\[ \left . \begin{array} [c]{c}x_{1}=\theta \\ x_{2}=\dot{\theta }\end{array} \right \} \left . \begin{array} [c]{l}\dot{x}_{1}=\dot{\theta }\\ \dot{x}_{2}=0.8-0.5\dot{\theta }-\sin \theta \end{array} \right \} \begin{array} [c]{l}\dot{x}_{1}=x_{2}\\ \dot{x}_{2}=0.8-0.5x_{2}-\sin x_{1}\end{array} \] Hence\[\begin{pmatrix} \dot{x}_{1}\\ \dot{x}_{2}\end{pmatrix} =\begin{pmatrix} x_{2}\\ 0.8-0.5x_{2}-\sin x_{1}\end{pmatrix} =\begin{pmatrix} g\left ( x_{1},x_{2}\right ) \\ f\left ( x_{1},x_{2}\right ) \end{pmatrix} \] Solve for \(\begin{pmatrix} \dot{x}_{1}\\ \dot{x}_{2}\end{pmatrix} =\begin{pmatrix} 0\\ 0 \end{pmatrix} \) for equilibrium. Hence \(x_{2}=0\) and therefore \(x_{1}=\sin ^{-1}\left ( 0.8\right ) \).
Now we obtain the linearized state matrix \(A\) at the equilibrium point found. First we note that \(\frac{\partial g}{\partial x_{1}}=0,\frac{\partial g}{\partial x_{2}}=1,\frac{\partial f}{\partial x_{1}}=\frac{\partial }{\partial x_{1}}\left ( 0.8-0.5x_{2}-\sin x_{1}\right ) =-\cos x_{1}\) and \(\frac{\partial f}{\partial x_{2}}=-0.5\), hence\begin{align*} A & =\begin{pmatrix} \frac{\partial g}{\partial x_{1}} & \frac{\partial g}{\partial x_{2}}\\ \frac{\partial f}{\partial x_{1}} & \frac{\partial f}{\partial x_{1}}\end{pmatrix} _{x_{1}=\sin ^{-1}\left ( 0.8\right ) ,x_{2}=0}\\ & =\begin{pmatrix} 0 & 1\\ -\cos x_{1} & -0.5 \end{pmatrix} _{x_{1}=\sin ^{-1}\left ( 0.8\right ) ,x_{2}=0}\\ & =\begin{pmatrix} 0 & 1\\ -\cos \left ( \sin ^{-1}\left ( 0.8\right ) \right ) & -0.5 \end{pmatrix} \\ & =\begin{pmatrix} 0 & 1\\ -\cos \left ( 0.927295\right ) & -0.5 \end{pmatrix} \\ & =\begin{pmatrix} 0 & 1\\ -0.6 & -0.5 \end{pmatrix} \end{align*}
Hence find the eigenvalues, we obtain\begin{align*} \begin{vmatrix} -\lambda & 1\\ -0.6 & -0.5-\lambda \end{vmatrix} & =0\\ \lambda ^{2}+0.5\lambda +0.6 & =0 \end{align*}
Hence \[ \lambda _{1,2}=\left \{ -0.25+0.733\,14\allowbreak i,-0.25-0.733\,14\allowbreak i\right \} \] This is of the form \[ \lambda =\alpha \pm \beta i \] With \(\alpha <0\), \(,\)Hence stable, spiral in.
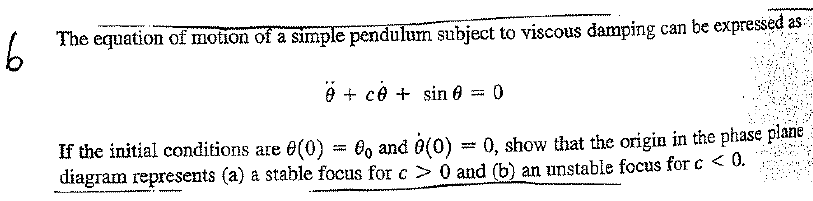
The equation is \[ \ddot{\theta }+c\dot{\theta }+\sin \theta =0 \] With IC \(\theta \left ( 0\right ) =\theta _{0}\),and \(\dot{\theta }\left ( 0\right ) =0\) Let\[ \left . \begin{array} [c]{c}x_{1}=\theta \\ x_{2}=\dot{\theta }\end{array} \right \} \left . \begin{array} [c]{l}\dot{x}_{1}=\dot{\theta }\\ \dot{x}_{2}=-c\dot{\theta }-\sin \theta \end{array} \right \} \begin{array} [c]{l}\dot{x}_{1}=x_{2}\\ \dot{x}_{2}=-cx_{2}-\sin x_{1}\end{array} \] Hence\[\begin{pmatrix} \dot{x}_{1}\\ \dot{x}_{2}\end{pmatrix} =\begin{pmatrix} x_{2}\\ -cx_{2}-\sin x_{1}\end{pmatrix} =\begin{pmatrix} g\left ( x_{1},x_{2}\right ) \\ f\left ( x_{1},x_{2}\right ) \end{pmatrix} \] Now, we are told to consider the initial condition \(\dot{\theta }=0\), but this is the same as \(\dot{x}_{1}=0\). But if speed is zero, then acceleration must also be zero, hence \(\ddot{\theta }=0\) or \(\dot{x}_{2}=0\). Therefore we need to solve for \(\begin{pmatrix} \dot{x}_{1}\\ \dot{x}_{2}\end{pmatrix} =\begin{pmatrix} 0\\ 0 \end{pmatrix} \) \(\ \) or \[\begin{pmatrix} x_{2}\\ -cx_{2}-\sin x_{1}\end{pmatrix} =\begin{pmatrix} 0\\ 0 \end{pmatrix} \] Therefore \(x_{2}=0\) and then \(\sin x_{1}=0\) or \(x_{1}=n\pi \) for \(n=0,\pm 1,\pm 2,\cdots \).
Now we obtain the linearized state matrix \(A\) at the equilibrium point found. First we note that \(\frac{\partial g}{\partial x_{1}}=0,\frac{\partial g}{\partial x_{2}}=1,\frac{\partial f}{\partial x_{1}}=-\cos x_{1}\) and \(\frac{\partial f}{\partial x_{2}}=-c\), hence\begin{align*} A & =\begin{pmatrix} \frac{\partial g}{\partial x_{1}} & \frac{\partial g}{\partial x_{2}}\\ \frac{\partial f}{\partial x_{1}} & \frac{\partial f}{\partial x_{2}}\end{pmatrix} _{x_{1}=n\pi ,x_{2}=0}\\ & =\begin{pmatrix} 0 & 1\\ -\cos x_{1} & -c \end{pmatrix} _{x_{1}=n\pi ,x_{2}=0}\\ & =\begin{pmatrix} 0 & 1\\ -\cos \left ( n\pi \right ) & -c \end{pmatrix} \end{align*}
Hence find the eigenvalues, we obtain\begin{align*} \begin{vmatrix} -\lambda & 1\\ -\cos \left ( n\pi \right ) & -c-\lambda \end{vmatrix} & =0\\ -\lambda \left ( -c-\lambda \right ) +\cos \left ( n\pi \right ) & =0\\ \lambda ^{2}+c\lambda +\cos \left ( n\pi \right ) & =0 \end{align*}
Now, we are asked to evaluate this at the center of the phase portrait, which means at \(x_{1}=0\) and \(x_{2}=0\), in other words, when \(n=0\) (since when \(n=0\), then \(x_{1}=0\)). Hence, when \(n=0,\) the characteristic equation becomes\[ \lambda ^{2}+c\lambda +1=0 \] Hence \[ \lambda _{1,2}=\left \{ \begin{array} [c]{c}-\frac{c}{2}+\sqrt{\frac{c^{2}}{4}-1}\\ -\frac{c}{2}-\sqrt{\frac{c^{2}}{4}-1}\end{array} \right \} \] We now consider all the possible values of \(c\) and see its effect on the roots of the characteristic equation. This is done using a table\[\begin{tabular} [c]{|l|l|l|l|}\hline $c$ value & roots form & Location of roots & type of stability at $\left ( 0,0\right ) $\\\hline $c<0$ and $\left \vert c\right \vert <2$ & $\alpha \pm i\beta $ where $\alpha >0$ & In RHS complex plane & Spiral out, UNSTABLE\\\hline $c<0$ and $\left \vert c\right \vert >2$ & $\alpha \pm \beta $ where $\alpha >0$ and $\beta <\alpha $ & In RHS on the real line & Repelling, UNSTABLE\\\hline $c>0$ and $\left \vert c\right \vert <2$ & $\alpha \pm i\beta $ where $\alpha <0$ & In LHS complex plane & Spiral in, STABLE\\\hline $c>0$ and $\left \vert c\right \vert >2$ & $\alpha \pm \beta $ where $\alpha <0$ and $\beta <\alpha $ & In LHS on the real line & Attracting, STABLE\\\hline \end{tabular} \ \] Therefore, we conclude that for \(c<0\) the system is unstable at equilibrium point \(\left ( 0,0\right ) \) and for \(c>0\) the system is stable at equilibrium point \(\left ( 0,0\right ) .\)
Notice that we did not use the initial condition on the position at all. i.e. knowing that \(\theta \left ( 0\right ) =\theta _{0}\) was not needed to solve this problem.

EQM is \[ \ddot{x}+f\frac{\dot{x}}{\left \vert \dot{x}\right \vert }+\omega _{n}^{2}x=0 \] We need to determine the phase plane trajectories. The term \(\frac{\dot{x}}{\left \vert \dot{x}\right \vert }\)will be either \(+1\) or \(-1\) depending on the sign of \(\dot{x}\)
Hence for \(\dot{x}>0\) we have\begin{align*} \ddot{x}+f+\omega _{n}^{2}x & =0\\ \ddot{x}+\omega _{n}^{2}x & =-f \end{align*}
And for \(\dot{x}<0\) we have\begin{align*} \ddot{x}-f+\omega _{n}^{2}x & =0\\ \ddot{x}+\omega _{n}^{2}x & =f \end{align*}
Analyze each case separately. For \(\dot{x}>0\) we have\begin{align*} \frac{d}{dt}\dot{x}+\omega _{n}^{2}x_{1} & =-f\\ \frac{dx_{2}}{dt}+\omega _{n}^{2}x_{1} & =-f\\ \frac{dx_{2}}{dx_{1}}\frac{dx_{1}}{dt}+\omega _{n}^{2}x_{1} & =-f\\ \frac{dx_{2}}{dx_{1}}x_{2}+\omega _{n}^{2}x_{1} & =-f\\ \frac{dx_{2}}{dx_{1}}x_{2} & =-f-\omega _{n}^{2}x_{1}\\ dx_{2}x_{2} & =\left ( -f-\omega _{n}^{2}x_{1}\right ) dx_{1} \end{align*}
Integrating both sides, we obtain\[ \frac{x_{2}^{2}}{2}=\left ( -fx_{1}-\frac{\omega _{n}^{2}x_{1}^{2}}{2}\right ) +C \] Using IC given by \(x_{1}\left ( 0\right ) =10\left ( \frac{f}{\omega _{n}^{2}}\right ) \) and \(x_{2}\left ( 0\right ) =0\), then the above becomes\begin{align*} 0 & =\left ( -f\times 10\left ( \frac{f}{\omega _{n}^{2}}\right ) -\frac{\omega _{n}^{2}\left [ 10\left ( \frac{f}{\omega _{n}^{2}}\right ) \right ] ^{2}}{2}\right ) +C\\ 0 & =-\frac{10f^{2}}{\omega _{n}^{2}}-50\omega _{n}^{2}\left ( \frac{f^{2}}{\omega _{n}^{4}}\right ) +C\\ C & =\frac{10f^{2}}{\omega _{n}^{2}}+50\frac{f^{2}}{\omega _{n}^{2}} \end{align*}
Hence\[ \fbox{$C=60\left ( \frac{f}{\omega _{n}}\right ) ^{2}$}\] Therefore, the phase portrait is \[ x_{2}^{2}=-2fx_{1}-\omega _{n}^{2}x_{1}^{2}+120\left ( \frac{f}{\omega _{n}}\right ) ^{2}\] Hence\[ \fbox{$x_{2}=\pm \sqrt{120\left ( \frac{f}{\omega _{n}}\right ) ^{2}-2fx_{1}-\omega _{n}^{2}x_{1}^{2}}$}\] Given \(f\) and \(\omega _{n}\) we can plot the phase plane. For \(\dot{x}<0\) we have\begin{align*} \frac{d}{dt}\dot{x}+\omega _{n}^{2}x_{1} & =f\\ \frac{dx_{2}}{dx_{1}}x_{2} & =f-\omega _{n}^{2}x_{1}\\ dx_{2}x_{2} & =\left ( f-\omega _{n}^{2}x_{1}\right ) dx_{1} \end{align*}
Integrating both sides, we obtain\[ \frac{x_{2}^{2}}{2}=\left ( fx_{1}-\frac{\omega _{n}^{2}x_{1}^{2}}{2}\right ) +C \] Using IC given by \(x_{1}\left ( 0\right ) =10\left ( \frac{f}{\omega _{n}^{2}}\right ) \) and \(x_{2}\left ( 0\right ) =0\), then the above becomes\begin{align*} 0 & =\left ( f\times 10\left ( \frac{f}{\omega _{n}^{2}}\right ) -\frac{\omega _{n}^{2}\left [ 10\left ( \frac{f}{\omega _{n}^{2}}\right ) \right ] ^{2}}{2}\right ) +C\\ C & =-\frac{10f^{2}}{\omega _{n}^{2}}+50\frac{f^{2}}{\omega _{n}^{2}} \end{align*}
Hence\[ \fbox{$C=40\left ( \frac{f}{\omega _{n}}\right ) ^{2}$}\] Therefore, the phase portrait is \begin{align*} \frac{x_{2}^{2}}{2} & =\left ( fx_{1}-\frac{\omega _{n}^{2}x_{1}^{2}}{2}\right ) +40\left ( \frac{f}{\omega _{n}}\right ) ^{2}\\ x_{2}^{2} & =2fx_{1}-\omega _{n}^{2}x_{1}^{2}+80\left ( \frac{f}{\omega _{n}}\right ) ^{2} \end{align*}
Hence\[ \fbox{$x_{2}=\pm \sqrt{80\left ( \frac{f}{\omega _{n}}\right ) ^{2}+2fx_{1}-\omega _{n}^{2}x_{1}^{2}}$}\] Given \(f\) and \(\omega _{n}\) we can plot the phase plane
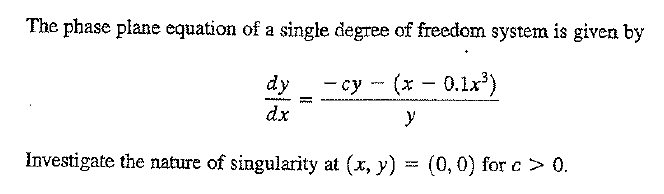
\[ \frac{dy}{dx}=\frac{-cy-\left ( x-0.1x^{3}\right ) }{y}\] From the above phase plane, obtain the differential equation, and then convert back to state space and obtain the system matrix.
Writing it in state space, where we take \(y=x_{2}\) and \(x=x_{1}\), we obtain\begin{align*} \frac{dx_{2}}{dx_{1}} & =\frac{-cx_{2}-\left ( x_{1}-0.1x_{1}^{3}\right ) }{x_{2}}\\ \frac{dx_{2}}{dx_{1}}x_{2} & =-cx_{2}-\left ( x_{1}-0.1x_{1}^{3}\right ) \\ \frac{dx_{2}}{dx_{1}}\frac{dx_{1}}{dt} & =-cx_{2}-\left ( x_{1}-0.1x_{1}^{3}\right ) \\ \frac{dx_{2}}{dt} & =-cx_{2}-\left ( x_{1}-0.1x_{1}^{3}\right ) \\ \ddot{x} & =-cx_{2}-\left ( x_{1}-0.1x_{1}^{3}\right ) \end{align*}
Hence the ODE is\[ \ddot{x}+c\dot{x}+\left ( x-0.1x^{3}\right ) =0 \] Therefore\[ \left . \begin{array} [c]{c}x_{1}=x\\ x_{2}=\dot{x}\end{array} \right \} \left . \begin{array} [c]{l}\dot{x}_{1}=\dot{x}\\ \dot{x}_{2}=-c\dot{x}-\left ( x-0.1x^{3}\right ) \end{array} \right \} \begin{array} [c]{l}\dot{x}_{1}=x_{2}\\ \dot{x}_{2}=-cx_{2}-\left ( x_{1}-0.1x_{1}^{3}\right ) \end{array} \] Hence\[\begin{pmatrix} \dot{x}_{1}\\ \dot{x}_{2}\end{pmatrix} =\begin{pmatrix} x_{2}\\ -cx_{2}-\left ( x_{1}-0.1x_{1}^{3}\right ) \end{pmatrix} =\begin{pmatrix} g\left ( x_{1},x_{2}\right ) \\ f\left ( x_{1},x_{2}\right ) \end{pmatrix} \] Hence, the linearized system matrix is, which we evaluate at \(\left ( 0,0\right ) \) is\[ A=\begin{pmatrix} \frac{\partial g}{\partial x_{1}} & \frac{\partial g}{\partial x_{2}}\\ \frac{\partial f}{\partial x_{1}} & \frac{\partial f}{\partial x_{2}}\end{pmatrix} _{x_{1}=0,x_{2}=0}\] But \(\frac{\partial g}{\partial x_{1}}=0,\frac{\partial g}{\partial x_{2}}=1,\frac{\partial f}{\partial x_{1}}=-1+0.3x_{1}^{2},\frac{\partial f}{\partial x_{2}}=-c\), hence\begin{align*} A & =\begin{pmatrix} 0 & 1\\ -1+0.3x_{1}^{2} & -c \end{pmatrix} _{x_{1}=0,x_{2}=0}\\ A & =\begin{pmatrix} 0 & 1\\ -1 & -c \end{pmatrix} \end{align*}
Hence\begin{align*} \begin{vmatrix} -\lambda & 1\\ -1 & -c-\lambda \end{vmatrix} & =0\\ \left ( -\lambda \right ) \left ( -c-\lambda \right ) +1 & =0\\ \lambda ^{2}-c\lambda +1 & =0 \end{align*}
Hence \[ \lambda _{1,2}=\left ( \begin{array} [c]{c}\frac{c}{2}+\sqrt{\frac{c^{2}}{4}-1}\\ \frac{c}{2}-\sqrt{\frac{c^{2}}{4}-1}\end{array} \right ) \] We set up the following table\[\begin{tabular} [c]{|l|l|l|l|}\hline $c$ value & roots form & Location of roots & type of stability at $\left ( 0,0\right ) $\\\hline $c>0$ and $\left \vert c\right \vert <2$ & $\alpha \pm i\beta $ where $\alpha >0$ & In RHS complex plane & Spiral out, UNSTABLE\\\hline $c>0$ and $\left \vert c\right \vert >2$ & $\alpha \pm \beta $ where $\alpha >0$ and $\beta <\alpha $ & In RHS on the real line & Repelling, UNSTABLE\\\hline $c<0$ and $\left \vert c\right \vert <2$ & $\alpha \pm i\beta $ where $\alpha <0$ & In LHS complex plane & Spiral in, STABLE\\\hline $c<0$ and $\left \vert c\right \vert >2$ & $\alpha \pm \beta $ where $\alpha <0$ and $\beta <\alpha $ & In LHS on the real line & Attracting, STABLE\\\hline \end{tabular} \ \] We see that for \(c>0\), system is UNSTABLE and depending on value of \(c\), it is either Spiral out or Repelling